python--实现Lorenz 63模式

通过python实现Lorenz 63模式(Lorenz,1963)：

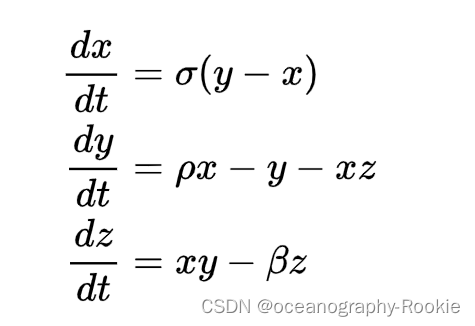
其中 σ , ρ 和 β 是参数，分别设置为10,28,8/3。 而x,y,z是模式状态变量，在模式中记为矢量 x→ 的三个元素 x1 , x2 , x3 可以使用数值方法求解常微分方程(欧拉法或者Runge-Kutta都可以，这里使用RK45方法)，从初值求得步长 δt 后的x状态：

def RK45(x,func,h):
    K1=func(x);
    K2=func(x+h/2*K1);
    K3=func(x+h/2*K2);
    K4=func(x+h*K3);
    x1=x+h/6*(K1+2*K2+2*K3+K4);
    return x1

def L63_rhs(x):
    # ODE右端项
    import numpy as np
    dx=np.ones_like(x);
    sigma=10.0; rho=28.0;beta=8/3;   # default parameters
    dx[0]=sigma*(x[1]-x[0])
    dx[1]=rho*x[0]-x[1]-x[0]*x[2];
    dx[2]=x[0]*x[1]-beta*x[2]
    return dx

def L63_adv_1step(x0,delta_t):
    # 使用RK45求解ODE，从初值x0求得步长delta_t后的x状态
    x1=RK45(x0,L63_rhs,delta_t)
    return x1

调用 L63_adv_1step 可以积分模式，测试以x0为初值积分5000步，图像如下，称为洛伦茨吸引子（蝴蝶效应）

import numpy as np
# 模式积分
x0 = np.array([1.508870, -1.531271, 25.46091])
Xtrue = np.zeros([3000,3]);Xtrue[0]=x0
delta_t=0.01
for j in range(1,3000):
    Xtrue[j] = L63_adv_1step(Xtrue[j-1],delta_t)
# 画图    
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
mpl.rcParams['legend.fontsize'] = 10
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(Xtrue[:,0], Xtrue[:,1], Xtrue[:,2],'r', label='Lorenz 63 model')
ax.legend()
plt.xlabel('x');plt.ylabel('y');
ax.set_zlabel('z')

Lorenz63模式具有强非线性，即使初值进行微小的扰动，也能对积分的结果造成巨大影响

# 模式积分
x0p = x0+0.001
Xctl = np.zeros([3000,3]);Xctl[0]=x0p
for j in range(1,3000):
    Xctl[j] = L63_adv_1step(Xctl[j-1],delta_t)
# 画图部分    
fig = plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.plot(Xtrue[range(1000),1], Xtrue[range(1000),2],'r', label='Truth')
plt.plot(Xtrue[0,1], Xtrue[0,2],'bx',ms=10,mew=3)
plt.plot(Xtrue[1000,1], Xtrue[1000,2],'bo',ms=10)
plt.ylim(0,50);plt.title('True',fontsize=15);plt.ylabel('z');plt.xlabel('y')
plt.text(5,25,r'$x_0$',fontsize=14)
plt.grid()
plt.subplot(1,2,2)
plt.plot(Xctl[range(1000),1], Xctl[range(1000),2],'g')
plt.plot(Xctl[0,1], Xctl[0,2],'bx',ms=10,mew=3,label='t0')
plt.plot(Xctl[1000,1], Xctl[1000,2],'bo',ms=10,label='t')
plt.ylim(0,50);plt.title('Control',fontsize=15);plt.ylabel('z');plt.xlabel('y')
plt.grid();plt.legend()
plt.text(5,25,r'$x_0+0.001$',fontsize=14)

"X"代表初始状态，左右两边的初值只相差0.001。模式积分不久，两边的差异就非常大了。 正是在于模式具有这种混沌性质，微小的初始偏差能够造成巨大的预报误差，需要使用同化手段利用现实的观测纠正模式，或者提供更精准的初值。

https://dafi.readthedocs.io/en/latest/tutorial_lorenz.html