PCL点云处理之点特征直方图(PFH)描述符（八十五）

一、PFH简介

随着点特征表示的发展，表面法线和曲率估计在表示特定点周围的几何形状方面有些不足。尽管计算速度极快且容易，但它们不能捕捉太多的细节，因为它们只用少量值来近似点的 k 邻域的几何形状。直接的结果是，大多数场景将包含许多具有相同或非常相似特征值的点，从而减少了它们的信息特征。本章介绍了一系列简单的3D 特征描述符，这些特征描述符被称为 PFH (点特征直方图)

二、理论基础

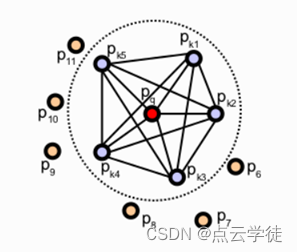
PFH 公式的目标是通过使用一个多维直方图的值来推广点周围的平均曲率来编码点的 k 邻域几何特性。这个高维超空间为特征表示提供了信息特征，对表面的6D 姿态是不变的，并且能够很好地处理邻域中存在的不同采样密度或噪声水平。点特征直方图表示基于 k 邻域中的点与其估计的表面法线之间的关系。简而言之，它试图通过考虑估计法线方向之间的所有相互作用来尽可能好地捕获采样表面的变化。因此，合成的超空间依赖于每个点的表面法线估计的质量。下图给出了一个查询点(p _ q)的 PFH 计算的影响区域图，用红色标记，放置在半径为 r 的圆(3D 球体)的中间，它的所有 k 邻居(距离小于半径 r 的点)在一个网格中完全互联。最终的 PFH 描述符被计算为邻域中所有点对之间关系的直方图，因此具有 O (k ^ 2)的计算复杂度。

为了计算两点 p i 和 p j 及其相关法线 n i 和 n j 之间的相对差，我们在其中一点定义了一个固定的坐标系(见