【信号与系统】（七）连续系统的时域分析 ——卷积积分

卷积积分

1 信号的时域分解

(1) 预备知识

直观看出

(2)任意信号分解

“0”号脉冲高度$f(0)$, 宽度为$\Delta$，用$p(t)$表示为： $f(0)\Delta p(t)$

“1”号脉冲高度$f(\Delta )$,宽度为$\Delta$，用$p(t-\Delta )$表示为： $f(\Delta )\Delta p(t-\Delta )$

“-1”号脉冲高度$f(-\Delta )$,宽度为$\Delta$, 表示为 $f(-\Delta )\Delta p(t+\Delta )$

上式就是卷积运算
$$\underset{\Delta \to 0}{\lim }：\Delta \to d\tau n\Delta \to \tau \sum \to \int$$
$$p(t-n\Delta )\to \delta (t-\tau )$$

2 任意信号作用下的零状态响应

信号先时域分解为冲激信号，再作用到系统。

---

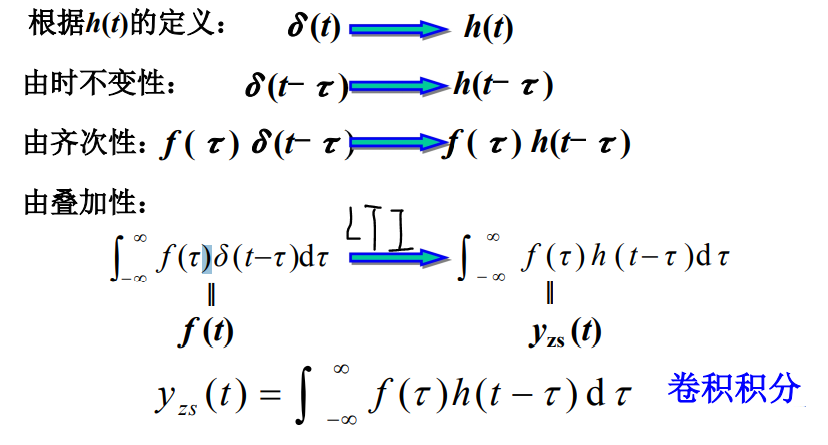
注意是关于$t$的函数$\tau$是参变量

3 卷积积分

——与信号分解的过程互逆的，卷积是通过两个函数和生成第三个函数的一种数学算子，且其中的函数不一定是冲激信号。

已知定义在区间$(–\infty ,\infty )$上的两个函数$f_1(t)$和$f_2(t)$，则定义积分

为$f_1(t)$与$f_2(t)$的卷积积分，简称卷积；记为

注意：积分是在虚设的变量$\tau$下进行的，$\tau$为积分变量，$t$为参变量。结果仍为$t$的函数。($t$用来对$f_2$定位，$\tau$用来对全局进行积分)可演变其他上下限.

• $f_1(t)=f_1(t)\epsilon (t)：{\int }_0^{+\infty }$
• $f_2(t)=f_2(t)\epsilon (t)：t>\tau ，{\int }_{-\infty }^t$
• $f_1(t)=\epsilon (t)，f_2(t)=\epsilon (t)：{\int }_0^t$

$\epsilon (t)：t>0$

4 卷积积分的图解法

卷积过程可分解为四步：

注意：$t$为参变量。

$f(t)=1/2，h(t)=t$

第四个图是的值是第三个图形的对应区间的面积
说明：

（1）图解法重在概念解释，一般适用于简单图形；

（2）求某一时刻卷积值时比较方便；

（3）确定积分的上下限是关键

5 卷积积分的代数性质

1 满足乘法的三律：

2 复合系统的冲激响应

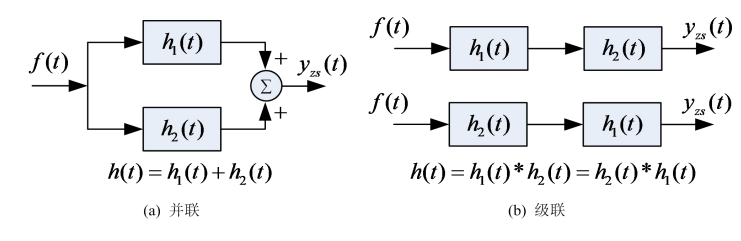
6 奇异函数的卷积特性

7 卷积的微积分性质

8 卷积的时移特性

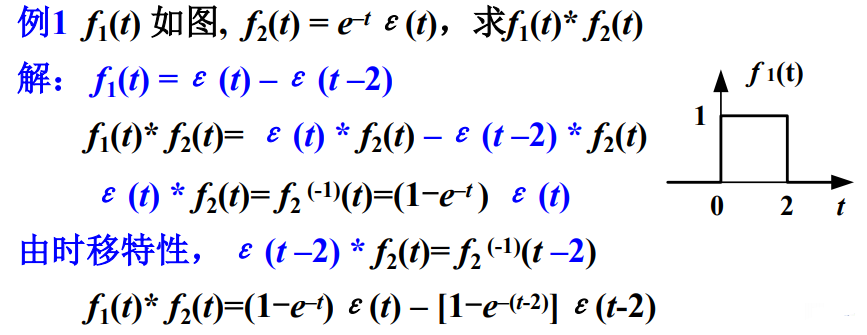
9 常用的卷积重要公式

10 卷积的多种求解方法

求解卷积的方法可归纳为：

(1)利用定义式，直接进行积分。对于容易求积分的
函数比较有效。如指数函数，多项式函数等。

(2)图解法。特别适用于求某时刻点上的卷积值。

(3)利用性质。比较灵活。

三者常常结合起来使用。

11 用梳状(comb)函数卷积产生周期信号

卷积的时移特性

周期为$T$的周期单位冲激函数序列，常称为梳状函数。

计算函数$f(t)$与${\delta }_T(t)$的卷积：

卷积的结果:
依然是周期信号，其周期为$T$。

讨论：
(1)当$T>\tau$ 时， $f_T(t)$中每个周期内的波形与 f (t) 相
同；
(2)若$T<\tau$ 时，各相邻脉冲之间将会出现重叠，将
无法使波形$f(t)$在$f_T(t)$的每个周期中重现。

$T>\tau ：$

12 矩形脉冲的卷积产生三角形和梯形脉冲

结论：两个不同宽的门函数卷积时，其结果为梯形函数，梯形函数的高度为窄门的门宽（面积），其上底为两个门函数宽度之差绝对值，下底为两个门函数宽度之和。

《工程信号与系统》作者：郭宝龙等
国家精品课程：信号与系统 ，中国大学MOOC，郭宝龙，朱娟娟