第三讲 GMM以及EM算法学习笔记

handsomeMB

已于 2022-08-25 15:11:58 修改

阅读量941

点赞数 1

分类专栏：语音识别学习文章标签：算法学习聚类

于 2022-07-21 19:10:07 首次发布

本文链接：https://blog.csdn.net/weixin_44589825/article/details/125918180

版权

语音识别学习专栏收录该内容

7 篇文章 1 订阅

订阅专栏

1.潜变量模型的学习

日常生活中，我们能够直接观测到的变量叫做观测变量。
与之对应，无法直接被观测到，需要通过模型和观测变量进行推断的变量就叫做潜变量。常用的潜变量模型就包括了GMM（高斯混合模型）和HMM（隐马尔可夫模型）。它们能够将将不完全数据（只有观测数据）的边缘分布转换成容易处理的完全数据（观测数据+潜变量）的联合分布。

2.K-Means聚类模型

K-Means聚类属于无监督学习算法，可以看作是一种特殊的，简化的混合高斯模型。它是将n个观测数据点按照一定标准划分到k个聚类中，数据点根据相似度划分。每一个聚类有一个质心，质心是对聚类中所有点的位置求平均值得到的点，每个观测点属于距离它最近的质心所代表的聚类。算法流程为1.先随机选择k个聚类质心。2.将每个观测点按照“距离”划分到离自己最近的质心并划分到此类。3.计算当前划分聚类的新质心。**重复第2，3步，直至达到收敛条件。**例如两次质心不再发生变化等。
通过K-Means聚类模型，可以对图像进行分割和压缩。

3.GMM模型和参数的估计 **

首先来复习一下高斯分布。高斯分布公式如下：

之所以选择高斯分布有两个原因，一个是因为高斯分布在自然界的数据中广泛存在。另一个是因为中心极限定理：在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。
然后是高斯模型的最大似然估计。
高斯分布的最大似然估计

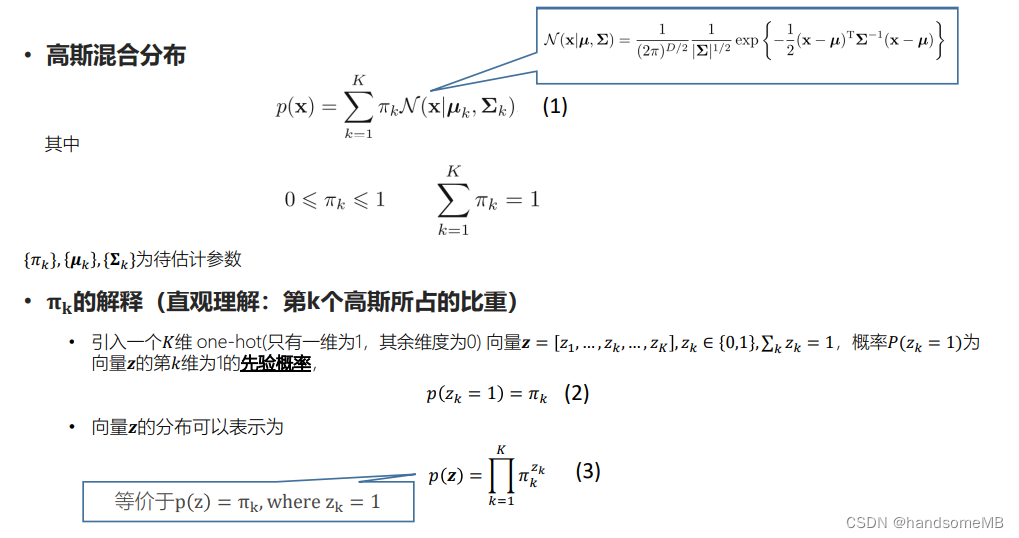
高斯混合分布
GMM模型使用EM算法得到的参数估计
GMM模型估计的EM算法
主要是公式的推导过程，需要自己多看几遍，有些地方还是不太懂。

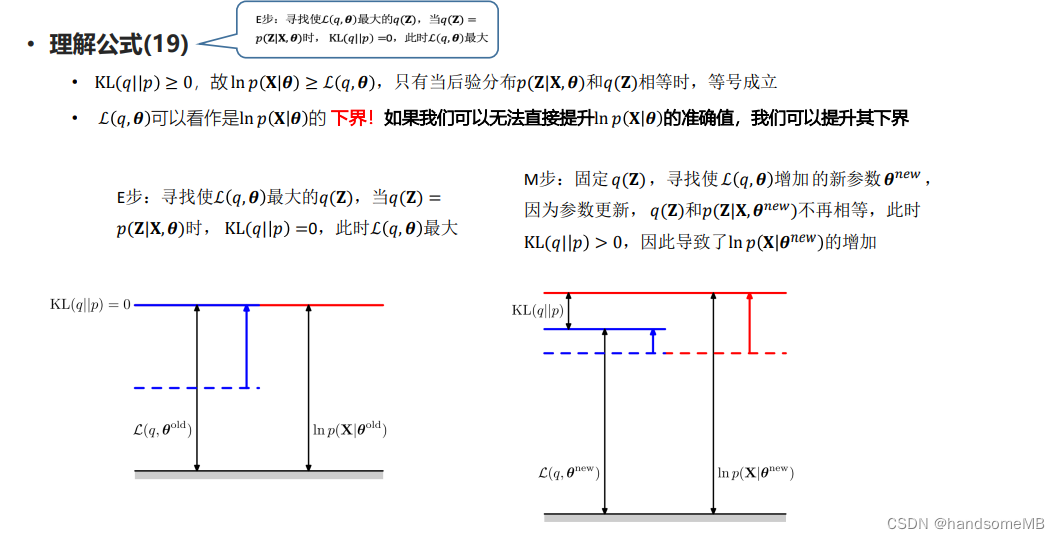
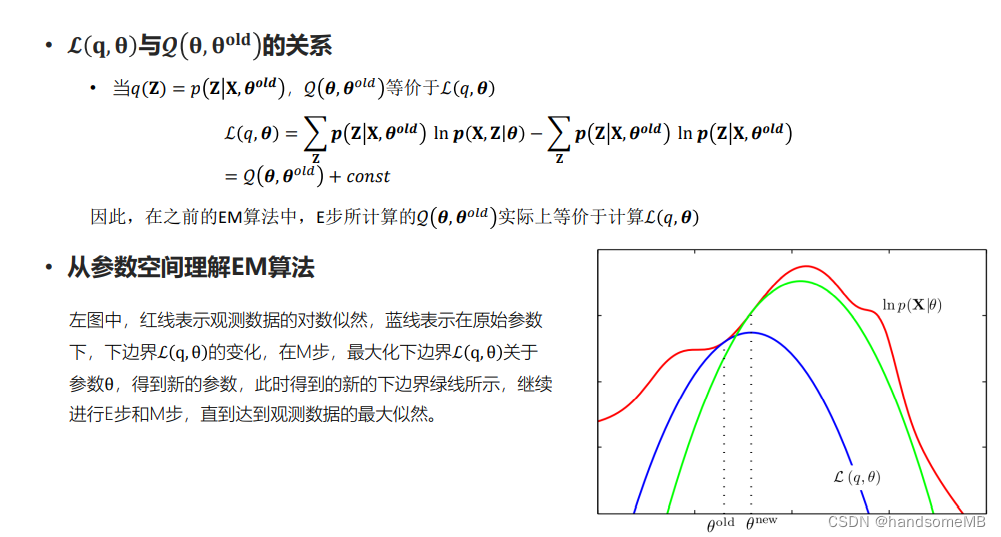
4.EM算法**

EM算法的通用步骤
利用迭代，在E步中求期望，在M步中最大化。关键是这个Q函数的构造。
EM算法的通用解释
EM算法的理解
从参数空间理解EM算法

5.总结

GMM模型与EM算法十分重要，但自己目前对于公式的推导还存在许多问题不能解决，课下应继续学习，与同学互相探讨。

6.作业代码

    # 计算对数似然函数
    def calc_log_likelihood(self, X):
        """Calculate log likelihood of GMM

            param: X: A matrix including data samples, num_samples * D
            return: log likelihood of current model 
        """

        log_llh = 0.0
        N = X.shape[0]
        for n in range(N):
            tmp = 0.0
            for k in range(self.K):
                tmp += self.pi[k] * self.gaussian(X[n], self.mu[k], self.sigma[k])
            log_llh += np.log(tmp)
        return log_llh

    # EM算法
    def em_estimator(self, X):
        """Update paramters of GMM

            param: X: A matrix including data samples, num_samples * D
            return: log likelihood of updated model 
        """

        log_llh = 0.0
        # X的shape为（1937，39）
        # 每一个小x的shape为（39，）
        # 首先构建一个（1937，5）的二维矩阵用于存放后验概率
        N = X.shape[0]
        gama = np.zeros((N, self.K))

        # 先遍历计算每一个后验概率的分子
        for n in range(N):
            for k in range(self.K):
                gama[n][k] = self.pi[k] * self.gaussian(X[n], self.mu[k], self.sigma[k])
        # 列相加计算对应的分母
        tmp = np.sum(gama, axis=1)
        for n in range(N):
            # 分子除分母
            gama[n] /= tmp[n]

        # 根据计算的后验概率重新估计参数
        # 首先计算Nk
        Nk = np.sum(gama, axis=0)

        # 更新pi,pi[k]所有元素之和应该为1
        self.pi = Nk/N

        # 更新mu,单个mu[k]的shape为（39，）
        self.mu = list()
        for k in range(self.K):
            tmp = np.zeros(self.dim)
            for n in range(N):
                tmp += X[n]*gama[n][k]
            tmp /= Nk[k]
            self.mu.append(tmp)

        # 更新sigma[k]  sigma[k]的shape为(39,39)
        self.sigma = list()
        for k in range(self.K):
            tmp = np.zeros((self.dim, self.dim))
            for n in range(N):
                tmp += gama[n][k] * np.outer(X[n]-self.mu[k], X[n]-self.mu[k])
            tmp /= Nk[k]
            self.sigma.append(tmp)

        # 计算似然估计
        log_llh = self.calc_log_likelihood(X)
        return log_llh