教程 | 回归如何控制混杂偏倚

回归分析主要研究目的可以归为三类：

• 探讨影响因素

• 控制偏倚

• 预测与分类

关于影响因素研究，郑老师的风暴统计平台已经更新了"线性回归分析"、"logistic回归分析"、"生存分析"三大板块，近日，又更新了 "回归控制混杂偏倚" 模块！

控制混杂的回归与探讨影响因素的回归，统计过程相似，但具体思路又有所不同，回归控制混杂分析中，无论焦点因素与结局是否存在关联，都会被纳入多因素模型。混杂偏倚控制的基本统计过程分为三步：

第一步，统计描述。描述人群的分布特征。

第二步， 简单关联性分析。针对目标暴露因素与结局（一因一果的探索性分析）。可以使用差异性分析（t、F、卡方、秩和）或单因素回归分析，两者结果大致相同。

第三步，多因素分析。 暴露因素与潜在混杂作为自变量（多因一果）构建多因素回归模型。

根据这个统计思路，下面为大家详细介绍一下风暴统计平台"回归控制混杂"模块的使用方式。

1. 进入风暴统计平台

首先，进入风暴统计平台，点击“风暴智能统计”—“回归控制混杂”—"最新版回归控制混杂"。

这里我们不再赘述数据的导入与整理过程，详细教程大家可以点击下方链接：

详细指南！风暴统计如何高效导入数据，统计分析快人一步？

详细版！如何利用风暴统计进行数据的整理转换？

2. 统计描述

统计描述方式，平台提供了两种：

① 分组差异性分析（多个变量在1个分类变量不同组中的分布特征）；

② 定量批量数据差异性分析（1个连续变量在多个不同分类变量中的分布特征）

这里多提一下分组差异性分析中的分组方式，会因不同研究类型而定

• 病例对照研究：一般按照病例组/对照组分组；

• 队列研究：通常按照暴露组/非暴露组分组；

• 横截面调查：可灵活处理；

• 随机对照研究：按照干预组/对照组分组。

2.1 / 分组差异性描述

风暴统计平台完成分组差异性描述十分的快捷，只需要依次在下拉框中勾选对应的分组变量、正态变量、偏态变量、分类变量。

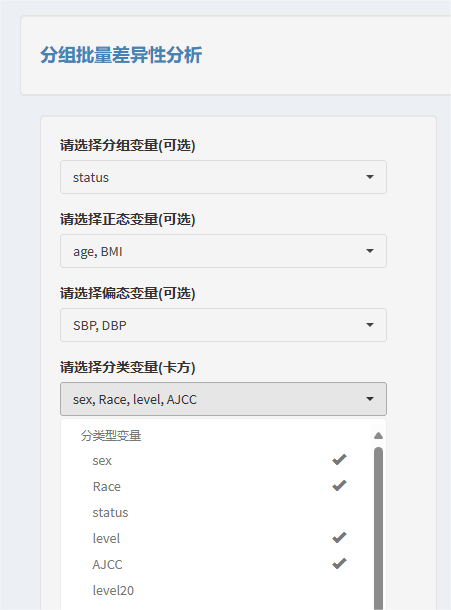
选择完毕后，右侧就会自动根据不同类型的数据，使用不同的分析方式生成结果三线表！

2.2 / 定量数据批量差异性描述

首先，选择定量检验变量，接着指定数据的分布类型是偏态还是正态。以及分组变量，被选择的变量将开展分组比较，定量数据的批量差异性分析只能选择分类数据哦！

选择完成后，右侧就更新了定量数据批量差异性分析三线表！

3. 简单关联性分析+多因素回归

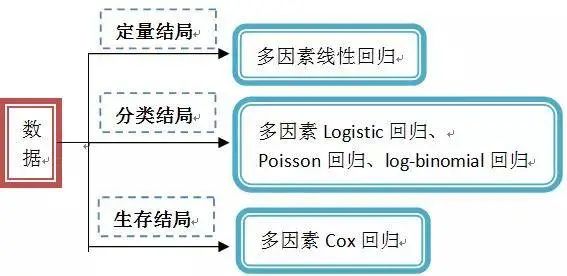
具体回归分析方法的选择，大家可以考虑以下包括的这几种，关于回归分析策略，平台给出了两种，下面会分别进行介绍：

• 多因素回归策略，一次性调整全部的混杂因素

• 多模型回归策略，通过3-5个模型逐步调整混杂，观察暴露与结局的关联性变化。

3.1 / 多因素回归策略

首先，选入模型的变量。（仅cox回归中会有随访时间变量）

从统计策略上讲，纳入多因素回归的协变量，可以是基线差异性分析有意义的变量，也可以是单因素回归分析有意义的变量。两种方法的结果大致相同，大家可以根据自己的研究设计进行选择。

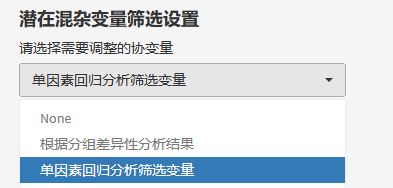
• 如果选择了基线差异性分析有意义的变量，那么平台会自动将上一步基线回归的结果同步到这里，减少操作步骤。
  

• 如果选择了单因素回归分析有差异的变量，需要再选择开展单因素回归的协变量（定量与分类全部选入）。(注：在指定分类自变量这里，平台会将分类少于5种的变量自动归入，如果有更多分类变量，需要手动修改哦！)

接着是多因素回归变量设置，包括P阈值，回归方法的选择。在影响因素研究中不太建议大家使用逐步回归（主要用在预测模型中）。

完成设置后，就可以生成回归三线表啦!可以看到因为AJCC是我们的焦点因素，因此，即便单因素AJCC与结局没有关联，已经会被自动纳入多因素回归中！

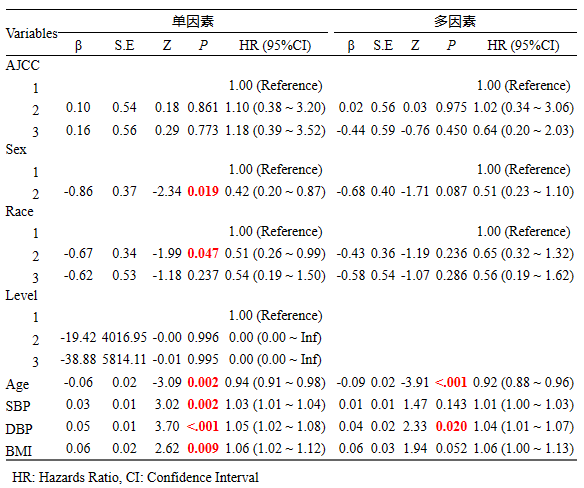
3.2 / 多模型回归策略

首先，选入模型的变量（仅cox回归中会有随访时间变量），接着点击"增加调整混杂因素"。

model1就是我们的单因素模型，因此我们直接开始选择model2的协变量，推荐使用自定义，多个模型逐个调整变量。

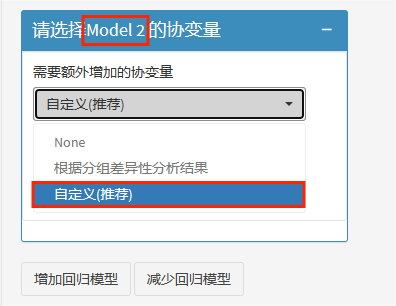
这里我们model2先矫正性别与年龄，接着，继续点击"增加回归模型"，model2矫正的性别、年龄会自动顺延至model3。另外，model3我们再额外矫正level和race。如需继续增加模型，可继续点击”增加回归模型“，最多可增至model5。

完成后，右侧就直接出现多模型的结果啦，包括脚注一应俱全！

以上就是，风暴统计平台"回归控制混杂"模块的全部使用教程啦！欢迎大家试用，如果您在风暴统计平台的使用过程中有任何的建议或疑问，可以加入我们的讨论群！群里郑老师与助教会在群内解答！

欢迎加入

统计机器人交流群