伴随矩阵：史上最通俗易懂的讲解！！

1. 什么是伴随矩阵

让我形象地解释伴随矩阵：

1. 转化过程的比喻
   想象原矩阵是一个魔方，伴随矩阵就是通过两步特殊旋转得到的新魔方：

• 第一次旋转：把每个小格子替换成它的"影响力"（代数余子式）
• 第二次旋转：把整个魔方转一个角度（转置操作）

1. 实际意义
   伴随矩阵就像是原矩阵的"最佳搭档"：

• 它们相乘会得到一个特殊的结果（原矩阵的行列式乘以单位矩阵）
• 这就像是找到了原矩阵的"完美配合伙伴"

1. 在求逆矩阵中的作用
   伴随矩阵就像是：

• 一个"翻译器"，帮助我们找到原矩阵的逆
• 只需要用伴随矩阵除以原矩阵的行列式，就得到了逆矩阵

1. 计算过程的形象理解
   在上面的可视化演示中：

• 第一步：看到原始矩阵
• 第二步：每个位置都变成了它的"影响力值"（代数余子式）
• 第三步：整个矩阵"转身"（转置），得到最终的伴随矩阵

1. 实际应用例子
   就像是：

• 在拼图游戏中，伴随矩阵帮我们找到每块拼图的正确位置
• 在平衡系统中，伴随矩阵告诉我们如何调整各个参数来达到平衡

伴随矩阵的美妙之处在于：

• 它保留了原矩阵的重要信息
• 但以一种新的方式重新组织了这些信息
• 这种重组让我们能够更容易地解决某些数学问题

2. 伴随矩阵是如何被发现的

伴随矩阵的发现是一个渐进的过程，它源于数学家们解决实际问题的需求。让我详细解释这个发现过程：

1. 早期基础（古代）

   • 最早可以追溯到古代中国和巴比伦的方程求解
   • 《九章算术》中已经包含了解线性方程组的方法
   • 这些早期工作为后来的发展奠定了基础

2. 关键突破（17-18世纪）

   • 莱布尼茨首次系统研究了行列式
   • 他发现了系数之间的特殊关系
   • 这些关系后来被证明与伴随矩阵密切相关

3. 理论形成（18世纪中期）

   • 克莱姆提出了著名的克莱姆法则
   • 这个发现揭示了行列式与方程解之间的关系
   • 这个关系实际上暗含了伴随矩阵的概念

4. 系统化研究（18世纪末-19世纪初）

   • 拉普拉斯深入研究了余子式
   • 他系统地发展了代数余子式理论
   • 这直接导致了伴随矩阵概念的形成

5. 现代发展（19世纪中期以后）

   • 凯利和西尔维斯特等人建立了现代矩阵理论
   • 伴随矩阵被纳入更广泛的代数结构中
   • 它的性质和应用得到了深入研究

伴随矩阵的发现过程表明：

• 它不是一蹴而就的，而是数学发展的必然产物
• 它源于解决实际问题的需要
• 多位数学家的工作共同促成了这个概念

有趣的是，伴随矩阵的发现过程展示了数学概念是如何从具体问题中抽象出来的：

1. 首先是解决具体的方程
2. 然后发现其中的规律
3. 最后形成抽象的理论

3. 伴随矩阵 可视化讲解

我来解释一下伴随矩阵的计算过程：

1. 伴随矩阵的定义：

   • 对于n阶矩阵A，其伴随矩阵$A^{\ast }$（或记作$adj(A)$）是由A的所有代数余子式转置而成的矩阵

2. 计算步骤：

   • 第一步：计算每个元素的代数余子式$A_{ij}$
   • 第二步：将代数余子式组成矩阵
   • 第三步：将该矩阵转置得到伴随矩阵

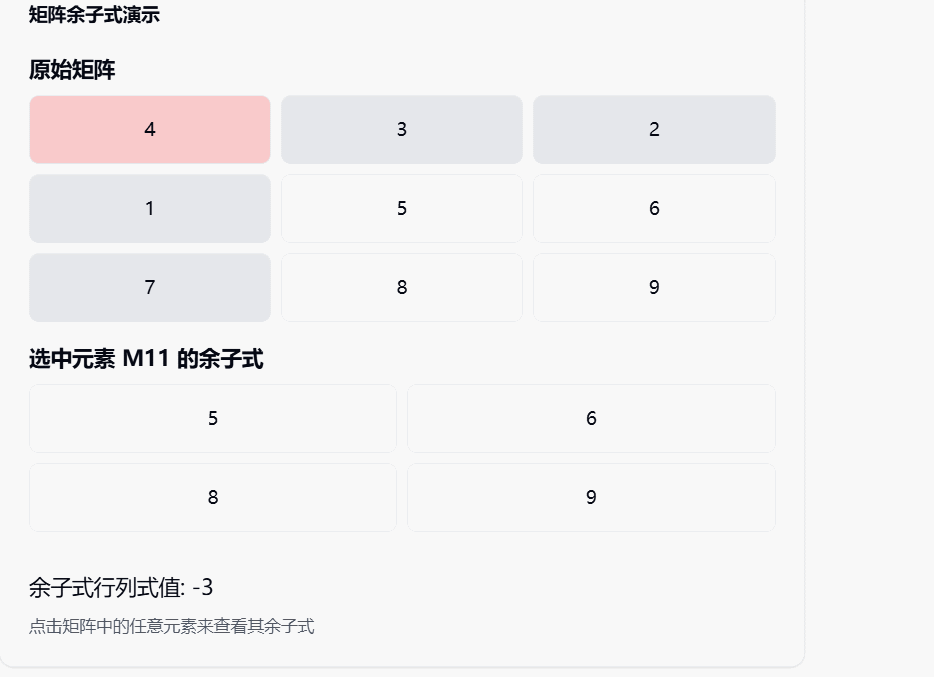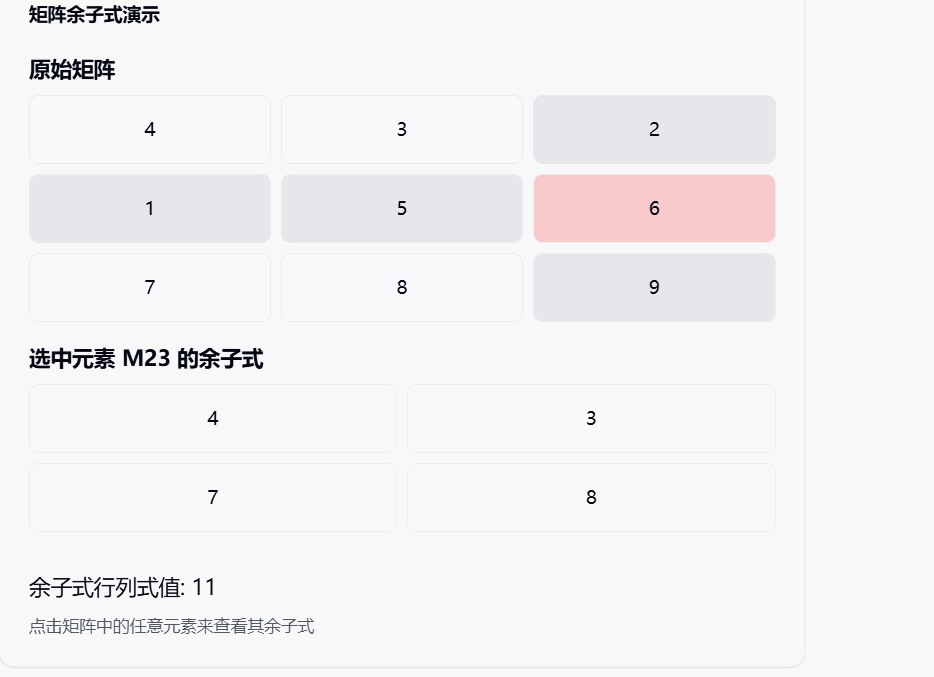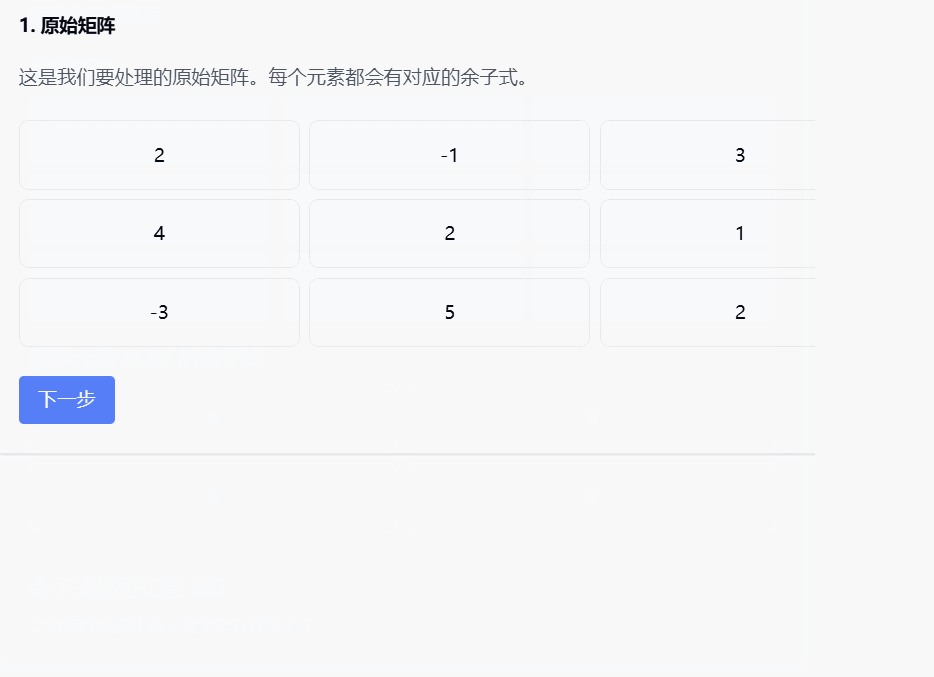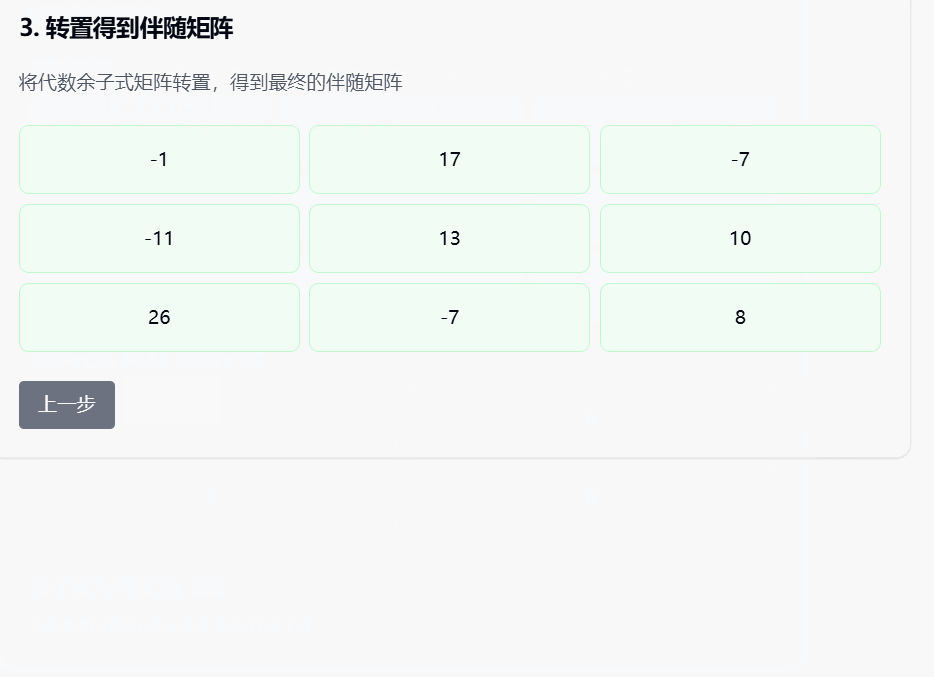
3. 在这个可视化工具中：

   • 你可以点击原矩阵中的任意元素，查看其余子式的计算过程
   • 可以看到代数余子式矩阵的形成
   • 通过按钮切换，查看最终的伴随矩阵（转置后的结果）

4. 伴随矩阵的重要性质：

   • 若A是可逆矩阵，则：$A^{-1}=\frac{1}{|A|}{A}^{\ast }$
   • 即矩阵的逆可以通过伴随矩阵计算得到

5. 使用方法：

   • 点击矩阵元素查看具体的余子式计算过程
   • 观察代数余子式矩阵的形成
   • 通过转置得到最终的伴随矩阵

这个可视化工具可以帮助你：

• 理解伴随矩阵的构造过程
• 掌握代数余子式到伴随矩阵的转换
• 直观地看到矩阵转置的效果

4. 伴随矩阵详解

基本定义

对于一个n阶方阵A，其伴随矩阵$A^{\ast }$（或记作adj(A)）是由A的代数余子式转置而成的矩阵。

计算步骤

1. 代数余子式矩阵

   • 对于矩阵A的每个元素$a_{ij}$，计算其代数余子式$A_{ij}$
   • $A_{ij}=(-1{)}^{i+j}{M}_{ij}$，其中$M_{ij}$是元素$a_{ij}$的余子式
   • 余子式$M_{ij}$是删除第i行和第j列后剩余元素构成的行列式

2. 转置

   • 将代数余子式矩阵进行转置，得到伴随矩阵

重要性质

1. 与原矩阵的关系：
   $A\cdot A^{\ast }=A^{\ast }\cdot A=|A|I$
   其中|A|是矩阵A的行列式，I是单位矩阵

2. 求逆矩阵：
   若A可逆，则：
   $A^{-1}=\frac{1}{|A|}{A}^{\ast }$

具体示例

让我们看一个2×2矩阵的例子：

设矩阵 $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$

1. 计算每个位置的代数余子式：

   • $A_{11}=d$
   • $A_{12}=-c$
   • $A_{21}=-b$
   • $A_{22}=a$

2. 转置得到伴随矩阵：
   $A^{\ast }=\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$

3×3矩阵的情况

对于3×3矩阵：
$$A=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$$

其伴随矩阵的每个元素都是2×2行列式。

应用场景

1. 求逆矩阵：当需要计算矩阵的逆时，伴随矩阵提供了一种有效的方法
2. 线性方程组求解：在克莱默法则中使用
3. 特征值计算：在某些特征值计算方法中会用到

注意事项

1. 伴随矩阵的计算量随矩阵阶数增加而急剧增加
2. 对于高阶矩阵，通常使用其他数值方法求逆，而不是通过伴随矩阵
3. 当矩阵接近奇异时，使用伴随矩阵求逆可能会导致数值不稳定