本文提出了一种新的GCN方法——GCNII,一种结合了初始残差(Initial residual)和恒等映射(Identity mapping)的普通GCN扩展模型,并证明了这两种技术有效的解决了过平滑的问题。
概要
GCNs是一种基于图结构的十分有用的深度学习方法。近年来,GCNs和它的变体在很多领域都取得了很好的成果。但是现有的GCNs方法大多都是浅层的,由于过平滑问题。在本文中,我们分析了GCNs网络设计的问题。我们提出了GCNⅡ,一种含有初始残差和恒等映射简单且有效方法的GCN变体,我们证明了GCNⅡ有效得解决了过平滑问题。
1. 介绍
GCNs相当于把CNNs应用于图结构的数据任务中。为了学习图表示,图卷积给所有的节点应用相同的线性变换,随后跟着一个非线性函数。进几年,GCNs和它的变体成功在很多地方都有成功应用。
虽然GCNs取得了很大的成功,但是大多数的GCN网路还是比较浅层的。最近的大多数模型,例如GCN和GAT,只用了两层就达到了最好的模型效果。如此浅层的模型限制了它们从高阶邻居中获取信息。然而,堆叠过多的层数和非线性变换会降低模型的表现。这种现象叫过平滑,具体来说就是随着层数的增加节点的表示会倾向于收敛到某个具体的值因此不可区分。ResNet在计算机视觉上使用残差连接解决了类似的问题,它在训练深层网络时是十分有效的。但是,把残差连接应用在GCNs只是缓解了过平滑的问题,最后的表现最好的模型仍然是GCN或GAT的两层模型。
过去有很多方法来尝试解决过平滑的问题:JKNet使用密集的跳跃连接来保持节点表示的局部性。DropEdge随机抛弃图中的一些边,缓解了过平滑问题。这两种方法能缓解随着层数增加模型表现下降的问题。但是对于半监督学习任务,最后的模型仍然使浅层的,层数增加给模型带来的好处仍然保持怀疑。
还有多种方法将深传播与浅层神经网络相结合:SGC在一层使用k阶平滑矩阵来捕获高阶信息。PPNP和APPNP使用个性化PageRank矩阵代替图卷积矩阵解决过平滑问题。GGDC(Klicperaet al.,2019b)通过将个性化PageRank(Page et al.,1999)推广到任意的图扩散过程,进一步扩展了APPNP。然而,这些方法在每一层使用线性聚合函数聚合邻居特征,失去了深层非线性结构的强大表达能力,这意味着它们仍然使浅层模型。
总之,如何设计一个真正深层的GCNs模型(没有过平滑并且有效)仍然是一个巨大的问题。在本文中,我们证明了普通GCN能通过两个简单且有效的改进(初始残差、恒等映射)扩展成到深层模型。初层残差从输入层构造了一个跳跃连接,恒等映射添加单位矩阵到权重矩阵中。我们证明了两个简单的技术解决了过平滑问题并且可以通过增加层数不断提高模型性能。GCNⅡ在多种半监督学习和全监督学习中取得了最好的模型效果。
其次,我们提供了GCNII模型的理论证明。通过堆叠k层,普通GCN本质上模拟了具有预定系数的k阶的多项式滤波器。wang指出这样一个滤波器模拟了一种懒惰的随机游走并且最终聚合到一种稳定的向量,所以导致了过平滑。从另一方面,我们证明了k层的GCNII模型能表达一个带着任意系数的多项式谱滤波器。这一性质对于设计深度神经网络至关重要。我们还导出了平稳向量的闭式并且对普通GCN进行了收敛速度分析。发现在一个多层的GCN模型中有高度数的节点更有可能过平滑。
2.准备工作
 表示
表示 个节点
个节点 条边。
条边。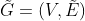 表示添加了自循环的图。
表示添加了自循环的图。 和
和 分别表示节点
分别表示节点 的度(
的度( 和
和 中)。
中)。 表示邻接矩阵而
表示邻接矩阵而 表示对角度矩阵。
表示对角度矩阵。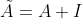 ,
,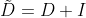 。
。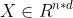 表示节点的特征表示。单个节点
表示节点的特征表示。单个节点 的特征表示为
的特征表示为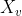 。归一化的拉普拉斯矩阵为
。归一化的拉普拉斯矩阵为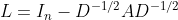 ,这是个带着自分解(
,这是个带着自分解(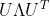 )的半正定矩阵。
)的半正定矩阵。 是L的特征值组成的对角矩阵。
是L的特征值组成的对角矩阵。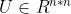 是一个由L特征向量组成的酉矩阵。
是一个由L特征向量组成的酉矩阵。 为信号向量,卷积核定义为
为信号向量,卷积核定义为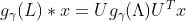 ,参数
,参数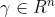 对应一个光谱滤波向量。
对应一个光谱滤波向量。
普通GCN
普通GCN表示卷积可以进一步近似于一个K阶的拉普拉斯多项式:
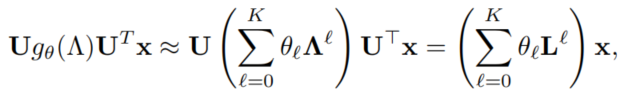
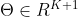 对应于一个多项式系数向量。普通GCN设置
对应于一个多项式系数向量。普通GCN设置 =1,
=1,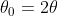 ,
,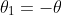 得到卷积操作
得到卷积操作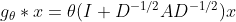 。最后,通过重整化技巧(the renormalization trick),通过
。最后,通过重整化技巧(the renormalization trick),通过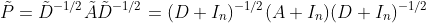 替换了
替换了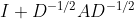 ,最终得到了图卷积层:
,最终得到了图卷积层:

 表示ReLU操作。
表示ReLU操作。
SGC文中表示通过堆叠K层,GCN相当于一个在 的图频域的固定K阶多项式滤波器。特别地,使用
的图频域的固定K阶多项式滤波器。特别地,使用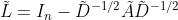 表示自连接图
表示自连接图 的归一化的拉普拉斯矩阵。因此,对一个信号
的归一化的拉普拉斯矩阵。因此,对一个信号 使用k层GCN相当于
使用k层GCN相当于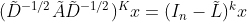 。wu证明了,通过给图添加自连接,
。wu证明了,通过给图添加自连接,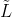 有效地缩小了底层图谱。
有效地缩小了底层图谱。
APPNP
Kllicpera使用个性化PageRank代表K阶固定滤波器。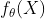 表示在特征矩阵
表示在特征矩阵 上的两层全连接神经网络的输出。PPNP表示为:
上的两层全连接神经网络的输出。PPNP表示为:
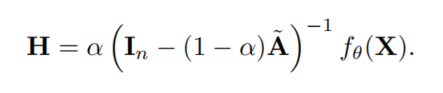
由于Personalized PageRank的优点,这个滤波器保存了局部性因此很适合于节点分类。
APPNP使用由截断幂迭代导出的近似值代替了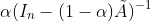 ,最后,带着K阶邻居的APPNP表示为:
,最后,带着K阶邻居的APPNP表示为:

![]()
通过解耦特征变换和传播,PPNP和APPNP能从高阶邻居中聚集信息而不需要增加神经网络的层数。
JKNet

JKNet会在最后结合所有层的表示来学习表示。不同的层代表了不同阶的信息。JKNet缓解了过平滑问题。
DropEdge
它随机丢弃了一些边,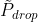 表示丢弃了一些边的重整化图卷积矩阵:
表示丢弃了一些边的重整化图卷积矩阵:

3.GCNII模型
我们定义l层的GCNII为:
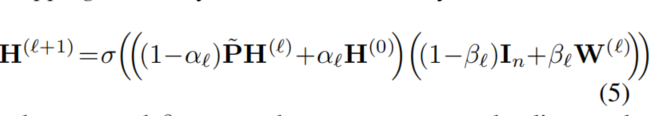
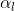 和
和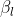 是两个超参数。
是两个超参数。
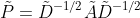 结合了重整化技巧的图卷积矩阵。
结合了重整化技巧的图卷积矩阵。
相比于GCN模型,我们做了两个修改:
1.我们结合了平滑特征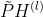 和初始残差连接到
和初始残差连接到 。
。
2.我们添加了一个自连接矩阵 到第
到第 层的权重矩阵
层的权重矩阵 。
。
初始残差连接:
在ResNet中的残差连接时结合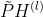 和
和 ,但是这种方法只能缓解过平滑的问题。随着模型层数的增加表现仍然会降低。
,但是这种方法只能缓解过平滑的问题。随着模型层数的增加表现仍然会降低。
我们提出了使用初始表示层 的残差,这样能保证即使堆叠了多层我们最后的表示仍然能有一部分(
的残差,这样能保证即使堆叠了多层我们最后的表示仍然能有一部分(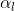 )来自初始层。在实际中,我们设置
)来自初始层。在实际中,我们设置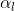 为0.1或者0.2所以最后一层的节点表示至少有小一部分是从输入特征中来的。并且
为0.1或者0.2所以最后一层的节点表示至少有小一部分是从输入特征中来的。并且 不一定要是特征矩阵
不一定要是特征矩阵 。如果特征的维度
。如果特征的维度 很大,我们可以使用一个全连接神经网络在
很大,我们可以使用一个全连接神经网络在 上来获取
上来获取 的低维向量表示
的低维向量表示 。
。
最后,APPNP使用了同样了初始残差网络,但是多层的非线性变换也会导致过平滑,因此,APPNP在不同层之间使用线性变换,仍然使一个浅层模型。说明只使用初始残差不足以使GCN扩展到一个深层模型。
恒等映射:
为了修复APPNP的缺点,我们从ResNet带来了恒等映射想法。在第 层,我们添加自连接矩阵到权重矩阵
层,我们添加自连接矩阵到权重矩阵 中。我们总结了我们这样做的动机:
中。我们总结了我们这样做的动机:
1.和ResNet一样,添加同一映射保证了GCNⅡ至少会和GCN的浅层模型一样的性能。尤其使,当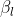 足够小,深层的GCNⅡ忽略了权重矩阵
足够小,深层的GCNⅡ忽略了权重矩阵 ,并且最终与APPNP一样。
,并且最终与APPNP一样。
2.不同维度的特征矩阵频繁交互会降低半监督学习任务的性能。将平滑表示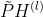 值直接映射到输出可以减少这种交互作用。
值直接映射到输出可以减少这种交互作用。
3.恒等映射在半监督学习中被证明是非常有效的。这被展示在线性ResNet中。
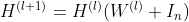 满足以下特性:1)最优的权重矩阵
满足以下特性:1)最优的权重矩阵 有更小的范数 2)唯一的临界点是全局最小值
有更小的范数 2)唯一的临界点是全局最小值
第一点允许我们时使用大的正则化在 中来防止过拟合,第二点当训练数据小时是有价值的
中来防止过拟合,第二点当训练数据小时是有价值的
4.Oono理论证明了第k层的节点特征会归一到同一表示,并且会导致信息丢失。聚合速度取决于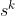 ,
, 是权重矩阵
是权重矩阵 的最大奇异值,通过把
的最大奇异值,通过把 替换成
替换成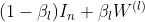 ,并且在
,并且在 上实施正则化,我们强迫的
上实施正则化,我们强迫的 范数是小的。
范数是小的。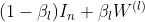 会很接近1,因此最大奇异值
会很接近1,因此最大奇异值 也会接近1。这意味这
也会接近1。这意味这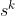 很大,信息丢失就会减少。
很大,信息丢失就会减少。
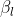 的设置原则是保证权重矩阵适应性的随着层数的增加而衰退。在实际中,我们设置(
的设置原则是保证权重矩阵适应性的随着层数的增加而衰退。在实际中,我们设置( 是超参数):
是超参数):
![]()
与迭代收缩阈值法的联系
近年来,有很多工作在基于优化的网络结构设计上。基本思想使全连接神经网络可以看成一种迭代优化算法来最小化一些函数,这是基于更好的优化算法可能导致更好的网络结构。在数值优化算法中的理论可能会激励更好的设计和更多可解释的网络结构。在我们结构中的恒等映射也被次激励。我们考虑LASSO:

类似于压缩感测,我们把 当作我们要恢复的信号,
当作我们要恢复的信号, 是测量矩阵,
是测量矩阵, 是我们观测到的节点特征。在我们的设置中,
是我们观测到的节点特征。在我们的设置中, 是节点的原始特征,
是节点的原始特征, 是需要在网咯中学习的节点嵌入。与标准的回归模型不同,
是需要在网咯中学习的节点嵌入。与标准的回归模型不同, 是需要通过回馈不断学习的矩阵。所以,这和稀疏编码问题是一样的,它被广泛用于设计和解释CNN中。迭代收缩阈值算法对解决上述优化问题是十分有效的,第
是需要通过回馈不断学习的矩阵。所以,这和稀疏编码问题是一样的,它被广泛用于设计和解释CNN中。迭代收缩阈值算法对解决上述优化问题是十分有效的,第 次更新为:
次更新为:
![]()
这里 是步大小,
是步大小,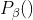 (
( )是入口软阈值函数:
)是入口软阈值函数:

现在,如果我们使用 重整化参数
重整化参数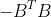 ,上述更新公式就和我们使用的非常像了。更有针对性,我们使用
,上述更新公式就和我们使用的非常像了。更有针对性,我们使用 ,这里
,这里表示初始残差连接,
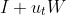 对应我们模型的恒等映射。软阈值算子相当于我们模型的非线性激活函数,相当于ReLU激活函数的作用。
对应我们模型的恒等映射。软阈值算子相当于我们模型的非线性激活函数,相当于ReLU激活函数的作用。
总之,我们的模型,尤其是恒等映射,是由求解套索问题的迭代收缩阈值算法中得到启发的。
4.频域分析
4.1多层GCN的频域分析
考虑了残差连接的GCN模型:

![]()
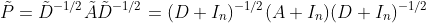 是使用了重整化技巧的图卷积矩阵。有人证明等式6相当于懒惰的随机游走带着转移矩阵
是使用了重整化技巧的图卷积矩阵。有人证明等式6相当于懒惰的随机游走带着转移矩阵![]() ,这懒惰的随机游走最后聚合到一个静止状态因此导致了过平滑。我们现在走进这个静止状态并且分析聚合速度。我们理论表明单个节点的聚合速度与节点的度有关,并且我们实验证明了这个发现。
,这懒惰的随机游走最后聚合到一个静止状态因此导致了过平滑。我们现在走进这个静止状态并且分析聚合速度。我们理论表明单个节点的聚合速度与节点的度有关,并且我们实验证明了这个发现。
定理1
假设![]() 连接了自己,
连接了自己,![]() 表示对图信号x使用了k层带着残差连接的重整化图卷积操作,
表示对图信号x使用了k层带着残差连接的重整化图卷积操作, 表示自连接图的
表示自连接图的 的光谱间隙,就是
的光谱间隙,就是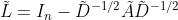
我们有以下结论
1)随着 趋向无穷,
趋向无穷,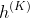 趋向于
趋向于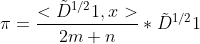 ,
, 表示全1向量
表示全1向量
2)聚合速度定义为:
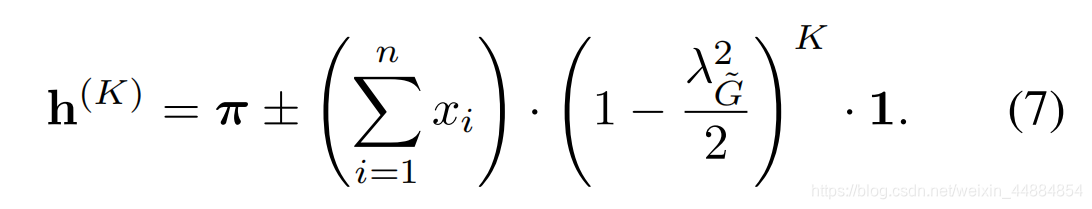
 和
和 表示原始图
表示原始图 的节点个数和边的个数。我们使用+-来表示对于每一个
的节点个数和边的个数。我们使用+-来表示对于每一个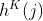 和
和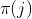 ,
, :
:

定理1有两个结果:
1)它表示第k层GCN的表示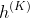 会会聚到一个向量
会会聚到一个向量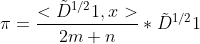 。这样的汇聚导致了过平滑,因为向量
。这样的汇聚导致了过平滑,因为向量 只包含两部分信息:每个节点的度,和初始信号的
只包含两部分信息:每个节点的度,和初始信号的 和向量
和向量 的内积。
的内积。
收敛速度和节点度
等式7表明会聚速度与特征条目的总和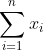 、光谱间隙
、光谱间隙 有关。若我们对单个节点的相对收敛速度近距离观测,我们能表示最后表示
有关。若我们对单个节点的相对收敛速度近距离观测,我们能表示最后表示 为:
为:

这表明如果一个节点 有一个很高的度
有一个很高的度 ,它的表示
,它的表示 会比静止状态
会比静止状态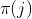 会聚得更快。更具次,我们得出以下猜想:
会聚得更快。更具次,我们得出以下猜想:
猜想1:度数越高的节点越容易受到过度平滑的影响。
4.2GCNII的频域分析
我们从频域角度考虑带自循环的图 。图信号
。图信号 的k阶多项式滤波器定义为:
的k阶多项式滤波器定义为: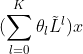 ,
,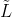 是图
是图 的归一化拉普拉斯矩阵,并且
的归一化拉普拉斯矩阵,并且 是多项式系数。wu证明了k层的GCN相当于带着固定系数
是多项式系数。wu证明了k层的GCN相当于带着固定系数 的k阶多项式。我们之后将会证明,固定的系数将会限制GCN的模型表现并导致过平滑。另一方面,我们证明了一个K层的GCNⅡ模型可以表示为带着任意系数的K阶多项式。
的k阶多项式。我们之后将会证明,固定的系数将会限制GCN的模型表现并导致过平滑。另一方面,我们证明了一个K层的GCNⅡ模型可以表示为带着任意系数的K阶多项式。
定理2:考虑带自环的图 和图信号
和图信号 。一个k层的GCNⅡ可以表示为一个带着任意系数
。一个k层的GCNⅡ可以表示为一个带着任意系数 的k阶多项式
的k阶多项式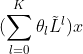
凭直觉,参数 允许GCNⅡ模拟多项式滤波器的系数
允许GCNⅡ模拟多项式滤波器的系数 。
。
表现力和过度平滑
使用带着任意系数的k阶多项式表达的本质是防止过平滑。为什么会这样,回顾定理1表明一个k层的普通GCN近似一个带着固定系数的k阶多项式滤波器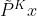 ,
,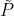 是重整化图卷积矩阵。过平滑是由于
是重整化图卷积矩阵。过平滑是由于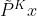 会聚到一个分布从而与输入特性
会聚到一个分布从而与输入特性 无关,因此引发梯度消失。DropEdge缓解了会聚的速率,但是随着
无关,因此引发梯度消失。DropEdge缓解了会聚的速率,但是随着 增加到无穷最后也没有用。
增加到无穷最后也没有用。
另一方面,定理二表明深层的GCNⅡ会聚到一个分布,这个分布携带了输入特征和图结构。凭此属性可确保GCNII不会遭受过度平滑的影响,即使层数变为无穷。更准确的说,定理二说明了 层的GCNⅡ能表示为
层的GCNⅡ能表示为 带着任意系数
带着任意系数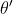 。正确的选择系数
。正确的选择系数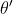 ,
,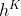 能同时携带着输入特征和图结构即使
能同时携带着输入特征和图结构即使 趋向于无穷。例如APPNP和GDC设置
趋向于无穷。例如APPNP和GDC设置对于某些常数
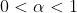 ,随着
,随着 趋向于无穷,
趋向于无穷, 会汇聚到向量
会汇聚到向量 的个性化PageRank,这是由邻接矩阵
的个性化PageRank,这是由邻接矩阵 和输入特征
和输入特征 的一个方程。在GCNⅡ和APPNP/GDC之间的差别有:1.模型中的向量
的一个方程。在GCNⅡ和APPNP/GDC之间的差别有:1.模型中的向量 是从输入特征和标签学习得来的。2.我们在每一层使用了激活函数Relu
是从输入特征和标签学习得来的。2.我们在每一层使用了激活函数Relu
5.其他相关工作
基于频域的GCN网络在近几年来非常火爆
6.实验



7.结论
我们提出了GCNII,一种简单并且深层的GCN模型来阻止过度平滑通过初始残差和同一映射。理论分析表明,该滤波器可以用任意系数的K阶的多项式来表示。对于多层的普通GCN模型,我们理论证明了高度数的节点更容易受到过平滑的。实验证明了深层GCNII达到了新的最好状态在很多半监督和全监督学习任务中。未来工作的有趣方向是结合attention机制并且分析GCNII与relu操作结合。
























 782
782

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








