一维小波函数
小波级数展开、离散小波变换、连续小波变换分别对应着傅里叶域里面的傅里叶级数展开、离散傅里叶变换、积分傅里叶变换
小波级数展开
对
f
(
x
)
∈
L
2
f(x) \in L^2
f(x)∈L2,可以在子空间
V
j
0
V_{j_0}
Vj0中用尺度函数展开和在子空间
W
j
0
,
W
j
0
+
1
,
⋯
W_{j_0},W_{j_0 + 1},\cdots
Wj0,Wj0+1,⋯中用某些数量的小波函数展开来表示:
f
(
x
)
=
∑
k
c
j
0
(
k
)
φ
j
0
,
k
(
x
)
+
∑
j
=
j
0
∞
∑
k
d
j
(
k
)
ψ
j
,
k
(
x
)
f(x) = \sum_kc_{j_0}(k)\varphi_{j_0,k}(x) + \sum_{j = j_0}^\infty\sum_kd_j(k)\psi_{j,k}(x)
f(x)=k∑cj0(k)φj0,k(x)+j=j0∑∞k∑dj(k)ψj,k(x)
其中
j
0
j_0
j0是任意的开始尺度,
c
j
0
(
k
)
c_{j_0}(k)
cj0(k)称为近似和或尺度系数,
d
j
(
k
)
d_j(k)
dj(k)称为细节和或小波系数,如果展开函数形成正交基或紧框架,那么系数可以如下计算:
c
j
0
(
k
)
=
<
f
(
x
)
,
φ
j
0
,
k
(
x
)
>
=
∫
f
(
x
)
φ
j
0
,
k
(
x
)
d
x
d
j
(
k
)
=
<
f
(
x
)
,
ψ
j
,
k
(
x
)
>
=
∫
f
(
x
)
ψ
j
,
k
(
x
)
d
x
c_{j_0}(k) = \left<f(x),\varphi_{j_0,k}(x)\right> = \int f(x)\varphi_{j_0,k}(x)dx \\ d_j(k) = \left<f(x),\psi_{j,k}(x)\right> = \int f(x)\psi_{j,k}(x)dx
cj0(k)=⟨f(x),φj0,k(x)⟩=∫f(x)φj0,k(x)dxdj(k)=⟨f(x),ψj,k(x)⟩=∫f(x)ψj,k(x)dx
如果展开函数是双正交基的一部分,这些等式中的
φ
,
ψ
\varphi,\psi
φ,ψ需要用其对偶函数来代替
离散小波变换
对应离散函数
f
(
n
)
=
f
(
x
0
+
n
Δ
x
)
,
n
=
0
,
1
,
2
,
⋯
,
M
−
1
f(n) = f(x_0 + n\Delta x),n = 0,1,2,\cdots,M-1
f(n)=f(x0+nΔx),n=0,1,2,⋯,M−1,对连续函数
f
(
x
)
f(x)
f(x)的小波级数展开系数就变为序列
f
(
n
)
f(n)
f(n)的正向离散小波变换DWT系数:
W
φ
(
j
0
,
k
)
=
1
M
∑
n
f
(
n
)
φ
j
0
,
k
(
n
)
W
ψ
(
j
,
k
)
=
1
M
∑
n
f
(
n
)
ψ
j
,
k
(
n
)
,
j
≥
j
0
W_{\varphi}(j_0,k) = \frac{1}{\sqrt M}\sum_nf(n)\varphi_{j_0,k}(n) \\ W_\psi(j,k) = \frac{1}{\sqrt M}\sum_n f(n)\psi_{j,k}(n),j \geq j_0
Wφ(j0,k)=M1n∑f(n)φj0,k(n)Wψ(j,k)=M1n∑f(n)ψj,k(n),j≥j0
在这些等式中,
φ
j
0
,
k
(
n
)
,
ψ
j
,
k
(
n
)
\varphi_{j_0,k}(n),\psi_{j,k}(n)
φj0,k(n),ψj,k(n)是基函数
φ
j
0
,
k
(
x
)
,
ψ
j
,
k
(
x
)
\varphi_{j_0,k}(x),\psi_{j,k}(x)
φj0,k(x),ψj,k(x)的取样形式,反向DWT是:
f
(
n
)
=
1
M
∑
k
W
φ
(
j
0
,
k
)
φ
j
0
,
k
(
n
)
+
1
M
∑
j
=
j
0
∞
∑
k
W
ψ
(
j
,
k
)
ψ
j
,
k
(
n
)
f(n) = \frac{1}{\sqrt M}\sum_kW_\varphi(j_0,k)\varphi_{j_0,k}(n) + \frac{1}{\sqrt M}\sum_{j = j_0}^\infty\sum_kW_\psi(j,k)\psi_{j,k}(n)
f(n)=M1k∑Wφ(j0,k)φj0,k(n)+M1j=j0∑∞k∑Wψ(j,k)ψj,k(n)
通常取
j
0
=
0
,
M
=
2
J
j_0 = 0,M = 2^J
j0=0,M=2J为2的幂,在上式中,
n
=
0
,
1
,
2
,
⋯
,
M
−
1
,
j
=
0
,
1
,
2
,
⋯
,
J
−
1
,
k
=
0
,
1
,
2
,
⋯
,
2
j
−
1
n = 0,1,2,\cdots,M-1,j = 0, 1,2,\cdots,J-1,k = 0,1,2,\cdots,2^j - 1
n=0,1,2,⋯,M−1,j=0,1,2,⋯,J−1,k=0,1,2,⋯,2j−1,对于哈尔小波,变换中采用的离散尺度和小波函数即基函数和之前
M
×
M
M \times M
M×M的哈尔变换矩阵的行相对应,上面的式子只对正交基和紧框架有效,对于双正交基,需要使用相应的对偶函数
连续小波变换
连续的平方可积函数
f
(
x
)
f(x)
f(x)的连续小波变换与实数值小波
ψ
(
x
)
\psi(x)
ψ(x)的关系定义为:
W
ψ
(
s
,
τ
)
=
∫
−
∞
∞
f
(
x
)
ψ
s
,
τ
(
x
)
d
x
W_{\psi}(s,\tau) = \int_{-\infty}^\infty f(x)\psi_{s,\tau}(x)dx
Wψ(s,τ)=∫−∞∞f(x)ψs,τ(x)dx
其中:
ψ
s
,
τ
(
x
)
=
1
s
ψ
(
x
−
τ
s
)
\psi_{s,\tau}(x) = \frac{1}{\sqrt{s}}\psi\left(\frac{x - \tau}{s}\right)
ψs,τ(x)=s1ψ(sx−τ)
s
,
τ
s,\tau
s,τ分别是尺度参数和平移参数,给定
W
ψ
(
s
,
τ
)
W_\psi(s,\tau)
Wψ(s,τ),就可以使用连续小波反变换得到
f
(
x
)
f(x)
f(x):
f
(
x
)
=
1
C
ψ
∫
0
∞
∫
−
∞
∞
W
ψ
(
s
,
τ
)
ψ
s
,
τ
(
x
)
s
2
d
τ
d
s
f(x) = \frac{1}{C_\psi}\int_0^\infty\int_{-\infty}^\infty W_\psi(s,\tau)\frac{\psi_{s,\tau}(x)}{s^2}d\tau ds
f(x)=Cψ1∫0∞∫−∞∞Wψ(s,τ)s2ψs,τ(x)dτds
其中:
C
ψ
=
∫
−
∞
∞
∣
Ψ
(
μ
)
∣
2
∣
μ
∣
d
μ
C_\psi = \int_{-\infty}^\infty\frac{|\mathbf{\Psi}(\mu)|^2}{|\mu|}d\mu
Cψ=∫−∞∞∣μ∣∣Ψ(μ)∣2dμ
Ψ
(
μ
)
\mathbf{\Psi}(\mu)
Ψ(μ)是
ψ
(
x
)
\psi(x)
ψ(x)的傅里叶变换
快速小波变换FWT
类似于子带编码方案,首先考虑多分辨率详细的等式:
φ
(
x
)
=
∑
n
h
φ
(
n
)
2
φ
(
2
x
−
n
)
\varphi(x) = \sum_n h_\varphi (n)\sqrt{2}\varphi(2x - n)
φ(x)=n∑hφ(n)2φ(2x−n)
用
2
j
2^j
2j对
x
x
x尺度化,用
k
k
k对它平移,并令
m
=
2
k
+
n
m = 2k + n
m=2k+n,给出:
φ
(
2
j
x
−
k
)
=
∑
k
h
φ
(
n
)
2
φ
(
2
(
2
j
x
−
k
)
−
n
)
=
∑
n
h
φ
(
n
)
2
φ
(
2
j
+
1
x
−
2
k
−
n
)
=
∑
m
h
φ
(
m
−
2
k
)
2
φ
(
2
j
+
1
x
−
m
)
\begin{aligned} \varphi(2^j x - k) &= \sum_kh_\varphi(n)\sqrt{2}\varphi(2(2^jx - k) - n) \\ &= \sum_nh_\varphi(n)\sqrt{2}\varphi(2^{j + 1}x - 2k - n) \\ &= \sum_mh_\varphi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m) \end{aligned}
φ(2jx−k)=k∑hφ(n)2φ(2(2jx−k)−n)=n∑hφ(n)2φ(2j+1x−2k−n)=m∑hφ(m−2k)2φ(2j+1x−m)
相似的可以得到小波函数:
ψ
(
2
j
x
−
k
)
=
∑
m
h
ψ
(
m
−
2
k
)
2
φ
(
2
j
+
1
x
−
m
)
\psi(2^j x - k) = \sum_mh_\psi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m)
ψ(2jx−k)=m∑hψ(m−2k)2φ(2j+1x−m)
有小波定义式如下:
d
j
(
k
)
=
∫
f
(
x
)
2
j
2
ψ
(
2
j
x
−
k
)
d
x
d_j(k) = \int f(x)2^\frac j2\psi(2^j x - k)dx
dj(k)=∫f(x)22jψ(2jx−k)dx
综合起来:
d
j
(
k
)
=
∫
f
(
x
)
2
j
2
[
∑
m
h
ψ
(
m
−
2
k
)
2
φ
(
2
j
+
1
x
−
m
)
]
d
x
d_j(k) = \int f(x)2^\frac j2\left[\sum_mh_\psi(m - 2k)\sqrt{2}\varphi(2^{j + 1}x - m)\right]dx
dj(k)=∫f(x)22j[m∑hψ(m−2k)2φ(2j+1x−m)]dx
交换积分和求和的顺序:
d
j
(
k
)
=
∑
m
h
ψ
(
m
−
2
k
)
[
∫
f
(
x
)
2
j
+
1
2
φ
(
2
j
+
1
x
−
m
)
]
d_j(k) = \sum_m h_\psi(m - 2k)\left[\int f(x)2^{\frac{j + 1}{2}}\varphi(2^{j + 1}x - m)\right]
dj(k)=m∑hψ(m−2k)[∫f(x)22j+1φ(2j+1x−m)]
可以看到括号中的量为
j
0
=
j
+
1
,
k
=
m
j_0 = j + 1,k = m
j0=j+1,k=m时的
c
j
0
(
k
)
c_{j_0}(k)
cj0(k):
d
j
(
k
)
=
∑
m
h
ψ
(
m
−
2
k
)
c
j
+
1
(
m
)
d_j(k) = \sum_m h_\psi(m - 2k)c_{j + 1}(m)
dj(k)=m∑hψ(m−2k)cj+1(m)
也就是尺度
j
j
j的细节系数是尺度
j
+
1
j + 1
j+1的近似函数的系数,类似的可以得到:
c
j
(
k
)
=
∑
m
h
φ
(
m
−
2
k
)
c
j
+
1
(
m
)
c_j(k) = \sum_mh_\varphi(m - 2k)c_{j + 1}(m)
cj(k)=m∑hφ(m−2k)cj+1(m)
当
f
(
x
)
f(x)
f(x)为离散函数的时候,因为小波级数展开的系数
c
j
(
k
)
,
d
j
(
k
)
c_j(k),d_j(k)
cj(k),dj(k)变为DWT的系数
W
φ
(
j
,
k
)
,
W
ψ
(
j
,
k
)
W_\varphi(j,k),W_\psi(j,k)
Wφ(j,k),Wψ(j,k),所以:
W
ψ
(
j
,
k
)
=
∑
m
h
ψ
(
m
−
2
k
)
W
φ
(
j
+
1
,
m
)
W
φ
(
j
,
k
)
=
∑
m
h
φ
(
m
−
2
k
)
W
φ
(
j
+
1
,
m
)
W_\psi(j,k) = \sum_mh_\psi(m - 2k)W_\varphi(j + 1,m) \\ W_\varphi(j,k) = \sum_mh_\varphi(m - 2k)W_\varphi(j + 1, m)
Wψ(j,k)=m∑hψ(m−2k)Wφ(j+1,m)Wφ(j,k)=m∑hφ(m−2k)Wφ(j+1,m)
上式揭示了相邻尺度DWT系数间的关系,DWT的系数
W
φ
(
j
,
k
)
,
W
ψ
(
j
,
k
)
W_\varphi(j,k),W_\psi(j,k)
Wφ(j,k),Wψ(j,k)可以用
W
φ
(
j
+
1
,
k
)
W_\varphi(j + 1, k)
Wφ(j+1,k)分别与顺序倒置尺度和小波向量
h
φ
(
−
n
)
,
h
ψ
(
−
n
)
h_\varphi(-n),h_\psi(-n)
hφ(−n),hψ(−n)进行卷积操作,然后对结果进行下采样来计算:
W
ψ
(
j
,
k
)
=
h
ψ
(
−
n
)
★
W
φ
(
j
+
1
,
n
)
∣
n
=
2
k
,
k
≥
0
W
φ
(
j
,
k
)
=
h
φ
(
−
n
)
★
W
φ
(
j
+
1
,
n
)
∣
n
=
2
k
,
k
≥
0
W_\psi(j,k) = h_\psi(-n) ★ W_\varphi(j + 1, n)|_{n = 2k,k\geq 0} \\ W_\varphi(j,k) = h_\varphi(-n) ★ W_\varphi(j + 1, n)|_{n = 2k,k\geq 0}
Wψ(j,k)=hψ(−n)★Wφ(j+1,n)∣n=2k,k≥0Wφ(j,k)=hφ(−n)★Wφ(j+1,n)∣n=2k,k≥0
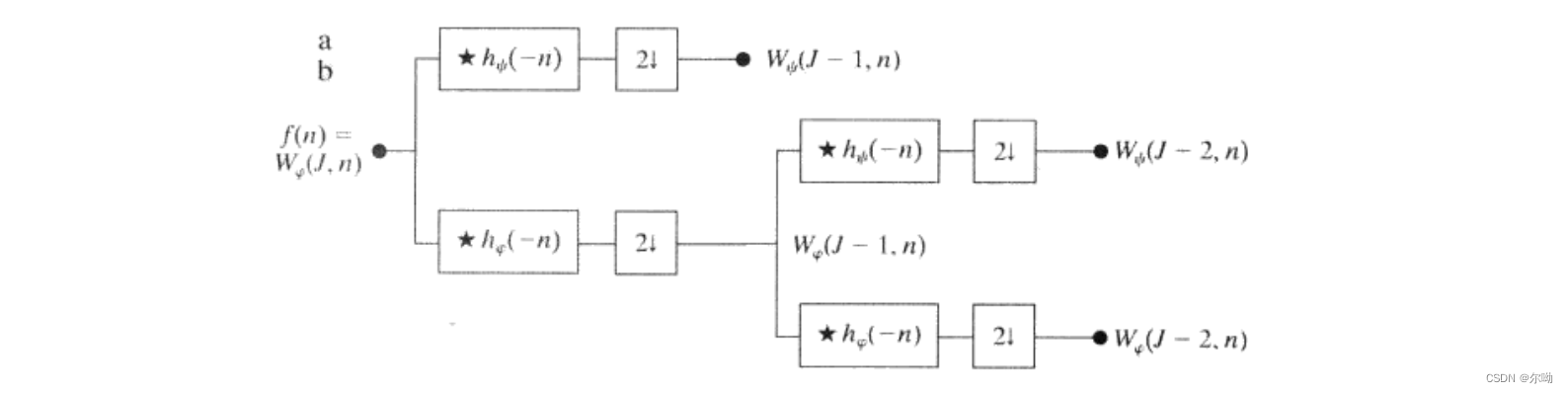
上述过程和子带编码类似,
h
0
(
n
)
=
h
φ
(
−
n
)
,
h
1
(
n
)
=
h
ψ
(
−
n
)
h_0(n) = h_\varphi(-n),h_1(n) = h_\psi(-n)
h0(n)=hφ(−n),h1(n)=hψ(−n),得到的
W
φ
(
j
,
k
)
,
W
ψ
(
j
,
k
)
W_\varphi(j,k),W_\psi(j,k)
Wφ(j,k),Wψ(j,k)分别代表低通和高通分量,使用FWT约要求
O
(
M
log
2
M
)
O(M\log_2 M)
O(Mlog2M)次操作,通常,我们选择
f
(
x
)
f(x)
f(x)的
2
J
2^J
2J个样本,并用
P
P
P个滤波器组在尺度
J
−
1
,
J
−
2
,
⋯
,
J
−
P
J - 1,J - 2,\cdots,J - P
J−1,J−2,⋯,J−P处生成一个
P
P
P尺度FWT,首先计算最高尺度即
J
−
1
J - 1
J−1的系数,最后计算最低尺度
J
−
P
J - P
J−P的系数,假设
f
(
x
)
f(x)
f(x)的取样频率合适,那么取样样本时在该取样分辨率下的尺度系数的良好近似,可以作为起始高分辨率尺度系数的输入,类似的,我们可以得到从正变换的结果快速反变换结果,相当于二带宽子带编码的综合过程,由分析过程
h
0
(
n
)
=
h
φ
(
−
n
)
,
h
1
(
n
)
=
h
ψ
(
−
n
)
h_0(n) = h_\varphi(-n),h_1(n) = h_\psi(-n)
h0(n)=hφ(−n),h1(n)=hψ(−n),得到
g
0
(
n
)
=
h
0
(
−
n
)
=
h
φ
(
n
)
,
g
1
(
n
)
=
h
1
(
−
n
)
=
h
ψ
(
n
)
g_0(n) = h_0(-n) = h_\varphi(n),g_1(n) = h_1(-n) = h_\psi(n)
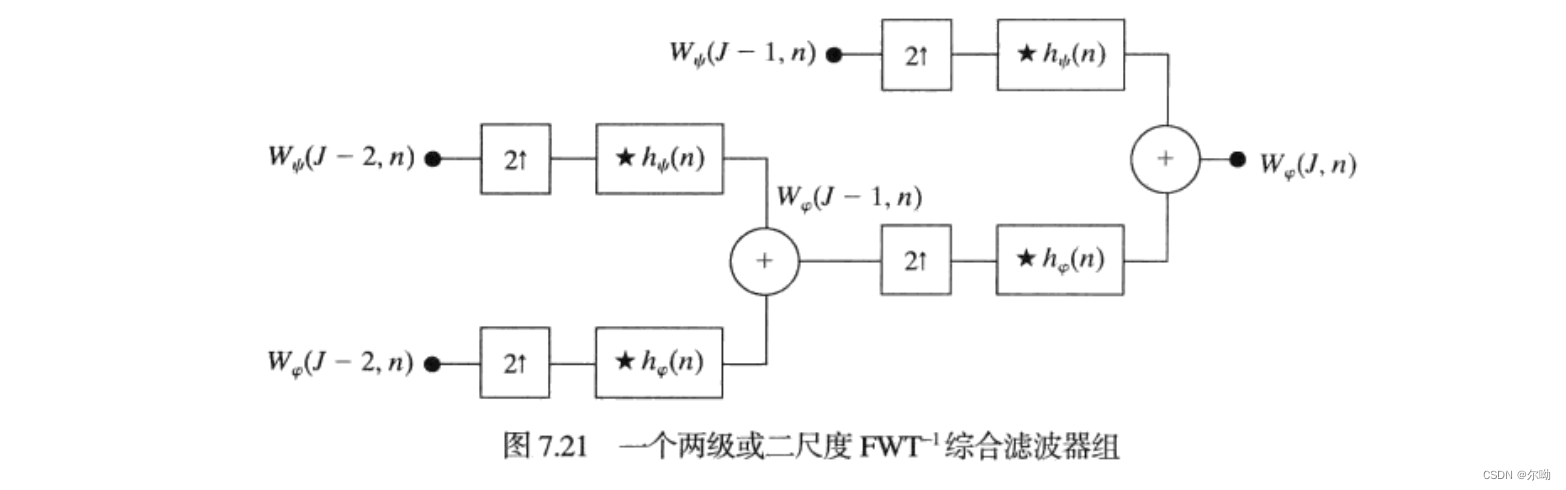
g0(n)=h0(−n)=hφ(n),g1(n)=h1(−n)=hψ(n),反变换
F
W
T
−
1
FWT^{-1}
FWT−1的滤波器组执行下述计算:
W
φ
(
j
+
1
,
k
)
=
h
φ
(
k
)
★
W
φ
2
↑
(
j
,
k
)
+
h
ψ
(
k
)
★
W
ψ
2
↑
(
j
,
k
)
∣
k
≥
0
W_\varphi(j + 1, k) = h_\varphi(k) ★ W_\varphi^{2\uparrow}(j,k) + h_\psi(k) ★ W_\psi^{2\uparrow}(j,k)|_{k \geq 0}
Wφ(j+1,k)=hφ(k)★Wφ2↑(j,k)+hψ(k)★Wψ2↑(j,k)∣k≥0
其中
W
2
↑
W^{2\uparrow}
W2↑表示基2的上取样,上取样通过插入0使得长度变为原来的两倍来完成的,之后上取样的系数和
h
φ
(
n
)
,
h
ψ
(
n
)
h_\varphi(n),h_\psi(n)
hφ(n),hψ(n)进行卷积完成滤波并相加产生较高尺度的近似,本质上创建了
f
(
n
)
f(n)
f(n)的较好近似
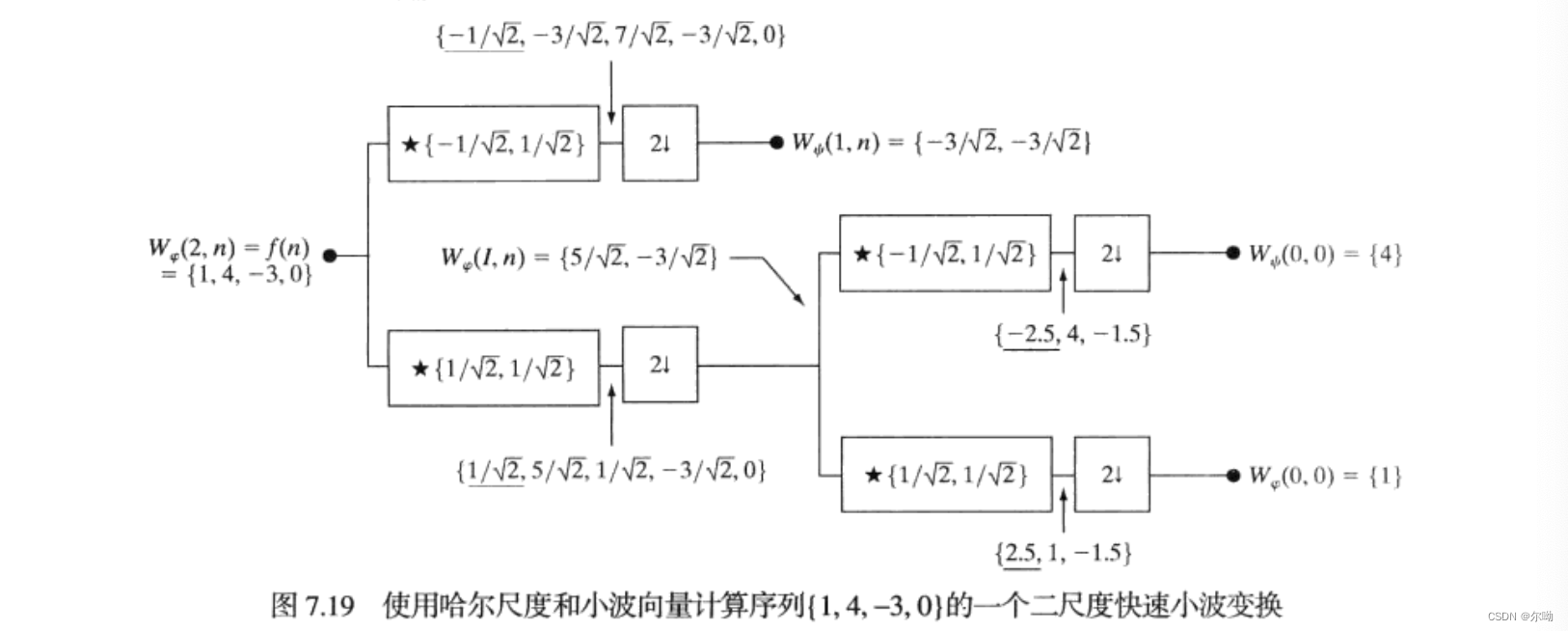
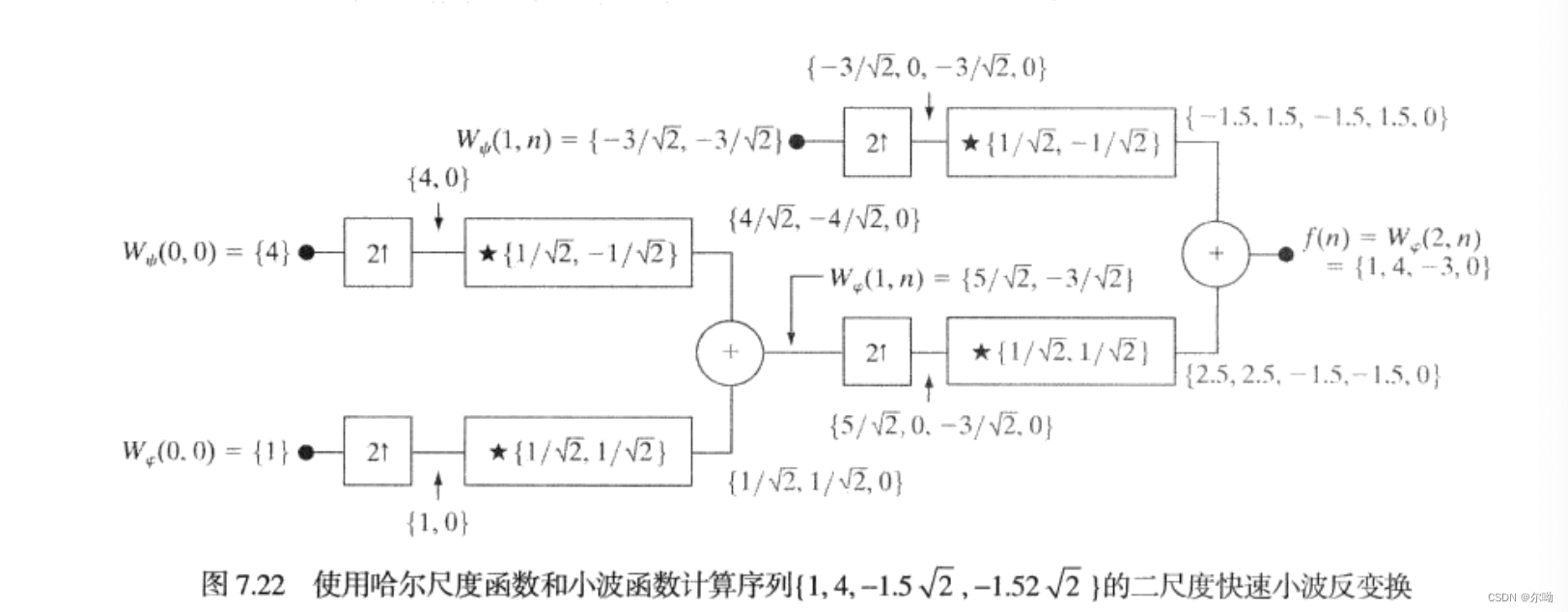
下面是两个示例过程:





















 837
837











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








