序言
什么是小波
“小波”（wavelet）就是一种“尺度”很小的波动，并具有时间和频率特性
小波函数必须满足以下两个条件：
（1）小波必须是振荡的；
（2）小波的振幅只能在一个很短的一段区间上非0，即是局部化的。如
■傅里叶变换的基础函数是正弦函数。
■小波变换基于一些小型波，称为小波，具有变化的频率和有限的持续时间。
◆傅里叶变换反映的是图像的整体特征, 其频域分析具有很好的局部性，但空间(时间)域上没有局部化功能。
◆与傅里叶变换相比，小波变换是空间(时间)和频率的局部变换，它通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节。
◆小波变换是基于具有变化的频率和有限持续时间的小型波进行的。它是多分辨率理论的分析基础。
◆多分辨率理论将多种学科的技术有效地统一在一起，其优势很明显某种分辨率下所无法发现的特性在另一种分辨率下将很容易被发现。
本文将从多分辨率的角度解释小波变换。
一、背景
◆物体的尺寸很小或者对比度不高的时候，通常采用较高的分辨率观察。
◆物体尺寸很大或者对比度很强，只需要较低的分辨率。
◆物体尺寸有大有小，强弱对比度同时存在，则适合用不同的分辨率对其进行研究。
1、图像金字塔
■以多分辨率来解释图像的一种简单有效的结构。一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低的图像集合。
■金字塔的底部是带处理图像的高分辨率表示，而顶部是低分辨率的近似。当向金字塔的上层移动时，尺寸和分辨率就降低。
基础级J的大小为NXN()
顶点级0的大小为1X1
第j级的大小为 (0≤j≤ J)共有J+1级，但是通常我们截短到P+1级，其中1≤P<J
➢J-1级近似输出用来建立近似值金字塔;作为金字塔基级的原始图像和它的P级减少的分辨率近似都能直接获取并调整;
➢J级的预测残差输出用于建立预测残差金字塔;近似值和预测残差金字塔都通过迭代计算获得。
迭代算法
1. 初始化，原始图象大小，j=J
2. j-1级，以2为步长进行子抽样，计算输入图像减少的分辨率近似值—j-1级近似值，生成子抽样金字塔。
3.对j-1 级近似值进行步长为2的内插，并进行过滤，生成与输入图像等分辨率的预测图像。
4.输入图像和预测图像之间的差异，产生预测残差金字塔。
5.重复2、3、4步骤。
2、子带编码
■子带编码也是多分辨率相关的重要图像技术。
■在子带编码中, 一幅图像被分解为一系列限带分量的几何，称为子带。
■子带可以重组在一起无失真地重建原始图象
■每个子带通过对输入进行带通滤波而得到
■子带带宽小于原始图像带宽，子带可以进行无信息损失的抽样
■原始图象的重建可以通过内插、滤波、和叠加单个子带来完成
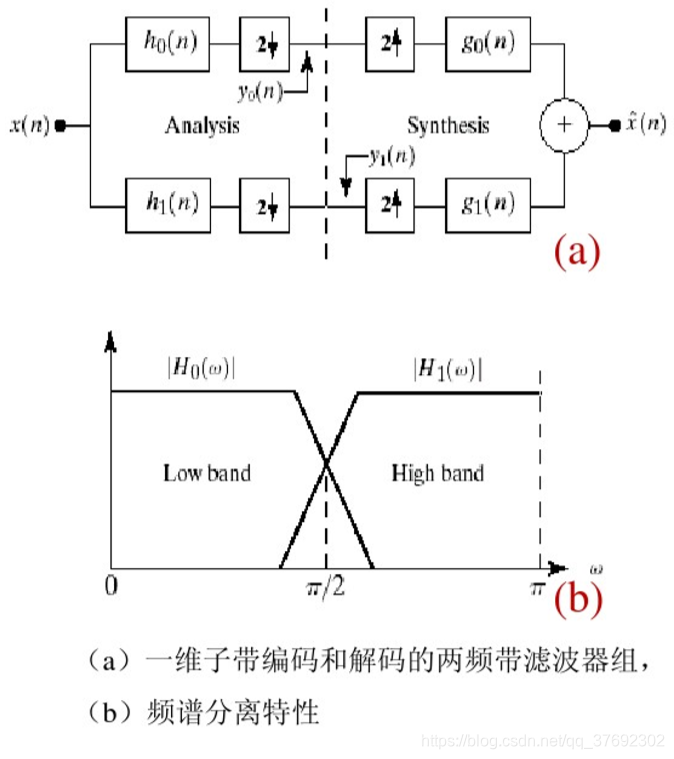
栗子：如下图，系统输入是一个一维的带限时间离散信号x(n)
■分析滤波器h0 (n)和h1(n)是半波数字滤波器，理想传输函数H0, H1如下图所示。
■H0低通滤波,输出x(n)的近似值
■H1高通滤波，输出x(n)的高频或细节部分
■综合滤波器go (n)和g1(n)
■ 为重构的结果
序列x(n)的Z变换
时域以2为因子的抽样对应到Z域
同样的，以2为因子的内插对应的变换为
x(n)先抽样再内插得到
系统输出
滤波器h0(n)的输出
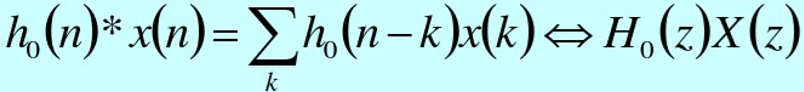
整理
注意：第二项含有-z，代表了抽样—内插过程带来的混叠。
对输入的无失真重建，假定下列条件：
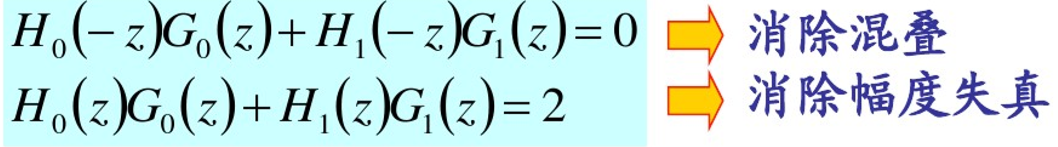
滤波器和综合滤波器双正交（证明略）
如下图，一维滤波器用于图像处理的二维可分离滤波器，可分离滤波器首先应用于某一维( 如水平方向)，在应
用于另一维(如垂直方向)
3、哈尔变换
它的基函数是最普遍也是最简单的正交小波，且哈尔变换本身对称、可分离，矩阵表示：,F是N*N图像矩阵，H是N*N变换的结果。
哈尔基函数：
二、多分辨率展开
◆图像金字塔、子带编码和哈尔变换，在数学理论多分辨率分析中扮演了重要角色。
◆在多分辨率分析( MRA )中，尺度函数被用于建立某一函数或图像的一系列近似值，相邻两近似值之间的近似度相差2倍。
◆被称为小波的附加函数用于对相邻近似值之间的差异进行编码
1、序列展开
信号或函数可以分解为一系列展开函数的线性组合
其中，k是有限或无限和的整数下标，是具有实数值的展开系数,
是具有实数值的展开函数
如果展开方式唯一，则任何指定的f (x)只有一个序列与之相对应
■称为基函数
■展开序列{}称为可表示这一类函数的基。
可展开的函数组成了一个函数空间，被称为展开集合的闭合跨度
其中。f(x)∈V表示f(x)属于{}跨度，可以写成
形式
系数ak可以通过内积得到
2、尺度函数
考虑整数平移和实数二值尺度、平方可积函,数φ (x)组成的可展开函数集合
k决定了
在x轴的位置
■j决定了
的宽度
■控制其高度或幅度
的形状随着j发生变化，φ (x)被称为尺度函数
通过选择适当的φ(x)，{}可以决定跨度, 所有可量度的平方可积函数的集合。
定义代表任何j，k上的跨度子空间
增大j，用于表示子空间函数的范围变窄；增加j将增加的大小，将允许具有变化较小的变量和较细节函数包含在子空间中。
3、小波变换
给定满足_MRA要求的尺度函数，能够定义小波函数ψ(x)(与它的积分变换及其二进制尺度)，跨越了相邻两个尺度子空间和
的差异
用尺度函数可得
如果f (x)=Wj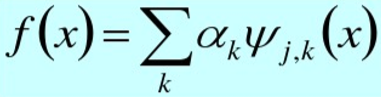
尺度函数与小波函数的关系
其中
表示空间并集中
的正交补集是Wj，
中所有成员对于Wj中的所有成员都正交
所有可量度的、平方可积函数空间表示为:
任何小波函数可以表示为平移的双倍分辨率尺度函数的加权和
其中
被称为小波函数系数;
为小波向量
利用小波跨越的正交补集空间、积分小波变换是正交的条件，可得
三、一维小波变换
1、小波序列展开
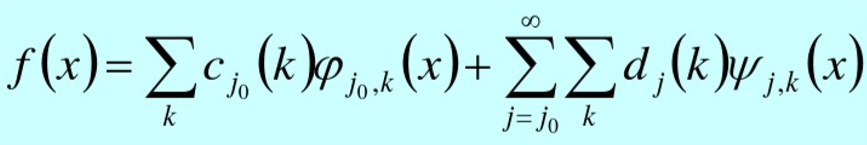
展开系数计算：
2、离散小波变换
3、连续小波变换
反连续小波变换
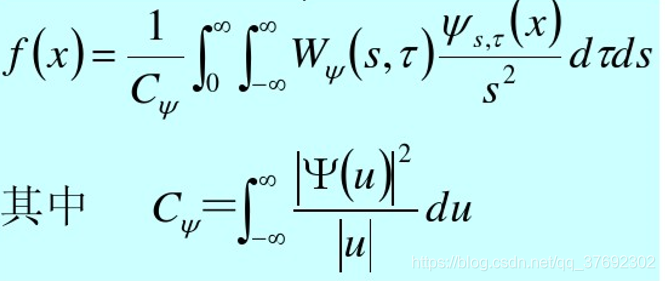
DWT和CWT的相似性
■连续变换参数T取代了 积分变换参数K
■连续尺度参数s与二进制尺度参数2j相反。
■连续尺度参数s出现在分母上，小波尺度和通常意义上的频率定义相反
■0 <s<1时，被压缩或宽度减小
■s>1时，扩大或展开
■CWT开始展开j0=-∞，消除了尺度函数间的明显关联
函数只包括小波项
■和DWT相似，CWT可以被看成是一-组变换系数
，它给出f(x)与基函数集
的相似性。
在连续情况下，两个集合都是无穷的
4、快速小波变换FWT
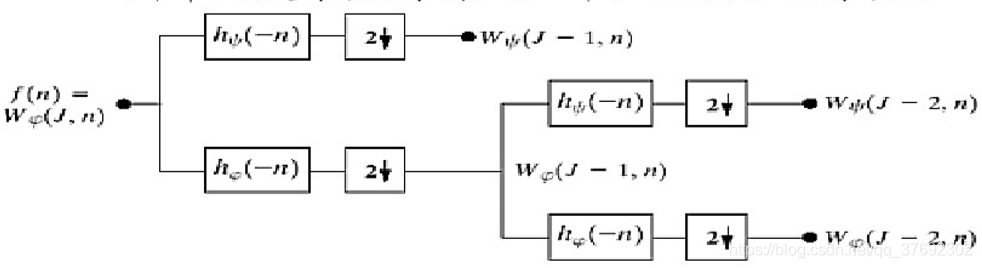
快速小波变换与FFT的比较
■ 运算的复杂性
对于FWT，长度为的序列的FWT的运算次数是0(M)阶，即:浮点乘法和加法(使用滤波器族)的次数与序列的长度存在这线性关系；FFT需要0 (MogM)阶。
■ 变换的基函数
傅里叶的基函数(正弦函数)保证了FFT的存在；FWT的存在取决于使用的小波函数的尺度函数是否存在，以及尺度函数和相应的小波函数的正交/双正交性
■ 表达函数时，时间和频率通常被作为不同的域来处理，它们之间存在这不可分割的关系
例如，要得到时域有价值的信息，就要忍受频域模糊，反之亦燃----海森伯测不准原理。块不重叠是正交基函数的特点。
■
■标准时域基给出时间发生的时刻，没有频域信息
■正弦基给出时间发生的频率但是没有时间分辨率
■FWT时间和频率分辨率是变化的
低频:块短而宽，即有较好的频率分辨率，对应较差的时间分辨率
高频:块窄而高，即有较高的时间分辨率，频率分辨率下降
四、二维小波变换
二维乘积可分离的尺度函数
二维可分离方向敏感小波
定义尺度和平移基函数
M*N的函数f(x,y)的离散小波变换
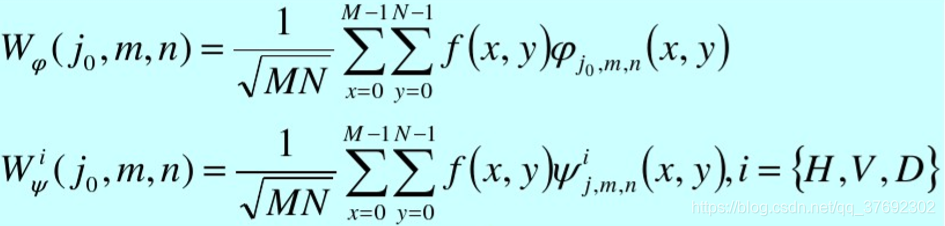
离散反小波变换
二维DWT可以用数字滤波器和抽样来实现
小波在图像处理中的用途，如在傅里叶域那样，基本方法是:
■计算一幅图像的二维小波变换
■修改变换
■计算反变换
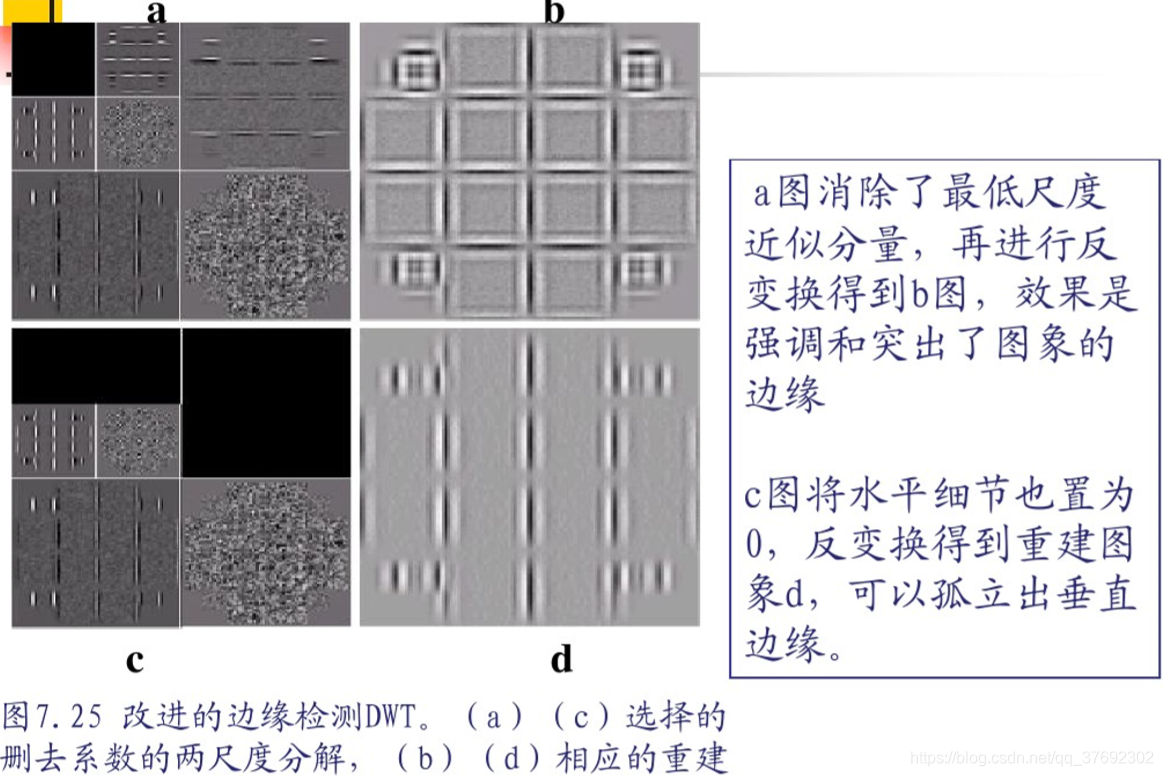
栗子：基于小波的边缘提取
五、小波包
■快速小波变换将一个函数分解为一系列与对数相关的频段
■低频被组成窄频段
■高频被组成宽频段
■想要较大的控制时频平面的一部分，FWT必须有更灵活的分解一一小波包
■产生过程的代价是FWT计算复杂度增加，从0 (M)到0 (M ogM)
三尺度FWT分析族、分析数和相应的频谱
■分析树提供了多尺度小波变换的紧凑有效的方法
■ 比对应的滤波器和基于子取样的方框图更容易画，并占有较少的空间
■ 相对容易定位有效分解
■三阶分析数提供了三种展开选择
六、小结
■小波变换是强有力的时频分析工具，是在克服傅立叶变换缺点的基础.上发展而来的。已成功应用于很多领域，如信号处理、图像处理、模式识别等。
■小波 变换的一个重要性质是它在时域和频域均具有很好的局部化特征，它能够提供目标信号各个频率子段的频率信息。这种信息对于信号分类是非常有用的。
■小波变换一个信号为一个小波级数，这样一个信号可由小波系数来刻画。
七、小波变换的应用
➢信号稀疏表示与重构;
➢信号、 图像去噪;
➢图像边缘检测、目标检测;
➢数据融合、 图像融合;
➢特征提取、模式识别;
➢红外图像背景抑制、 目标识别等。
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
