图像处理学习笔记-07-小波和多分辨率处理01

背景

图像金字塔

• 金字塔底部是图像的高分辨率表示，顶部是低分辨率表示，假设最底部基础级$J$的大小为$2^J\times 2^J$或$N\times N$，最顶部级0的大小为$1\times 1$即单个像素，一般图像金字塔没有那么多层，常见是$P+1$级，此时级数$j$的取值范围为$J-P,\cdots ,J-2,J-1,J$，因为过低的分辨率价值不大，$P+1$级金字塔的像素总数为:
  $$N^2\left(1+\frac{1}{(4{)}^1}+\frac{1}{(4{)}^2}+\cdots +\frac{1}{(4{)}^P}\right)\le =\frac{4}{3}{N}^2$$
• 创建近似和预测残差金字塔的一个简单系统如下图：
  
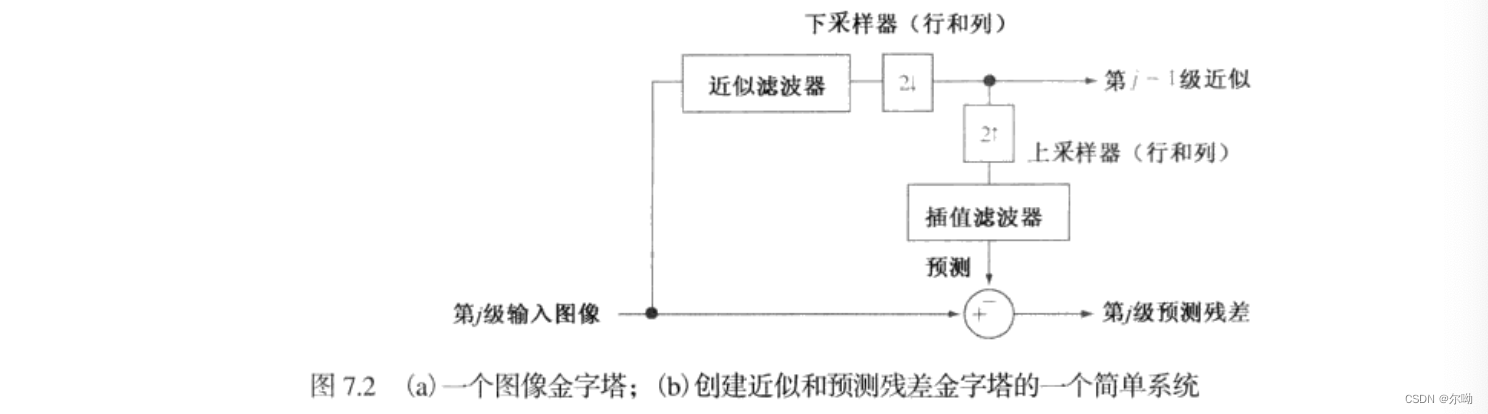
• 近似金字塔的第$j-1$级：将第$j$级的输入图像通过滤波然后进行以2为因数的下采样，当使用的滤波器是高斯滤波器时得到的是高斯金字塔
• 通过$j-1$级图像得到$j$级输入图像的估计：对近似金字塔的$j-1$级进行上采样和滤波，得到的图像和$j$的图像大小相同
• 预测残差金字塔的第$j$级：将近似金字塔的$j$级图像和上面得到的$j$级的估计相减

子带编码

简单数字滤波器由三部分组成，延迟单元、乘法器和加法器，其中延迟单元依次连接以建立输入序列$f(n)$的$K-1$延迟即右移的形式，输入序列$f(n)=f(n-0)$和延迟单元输出处的$K-1$个延迟序列表示为$f(n-1),f(n-2),\cdots ,f(n-K+1)$，分别与常数$h(0),h(1),\cdots ,h(K-1)$相乘，然后求和，可以产生求和之后的输出序列：
$$\hat{f}(n)=\sum _{k=-\infty }^{\infty }h(k)f(n-k)=f(n)★h(n)$$
以延迟序列$f(n-2)$为例：
$$f(n-2)=\{\begin{array}{ll}⋮& \\ f(0)& n=2\\ f(1)& n=3\\ ⋮& \end{array}$$
当$f(n)$使用冲激响应函数$\delta (n)$代替，则：
$$\hat{f}(n)=\sum _{k=-\infty }^{\infty }h(k)\delta (n-k)=h(n)$$
可以看到冲激响应的长度为K，这种滤波器称为有限冲激响应滤波器FIR，下图显示了6个功能上相关的滤波器的冲激响应：
$$\begin{array}{rl}{h}_1(n)& \\ h_2(n)& =-h_1(n)\\ h_3(n)& =h_1(-n)\\ h_4(n)& =h_1(K-1-n)\\ h_5(n)& =(-1{)}^n{h}_1(n)\\ h_6(n)& =(-1{)}^n{h}_1(K-1-n)\end{array}$$
其中$h_5(n)$是$h_1(n)$的调制形式，以上是对数字信号滤波的简要介绍。下图是一个两波段子带编码和解码系统：

滤波器组$h_0(n),h_1(n)$用于将输入序列分为两个半长序列$f_{lp}(n),f_{hp}(n)$，表示输入的子带，滤波器$h_0(n),h_1(n)$的理想传递特性如上右图所示，滤波器$h_0(n)$是一个低通滤波器，其输出子带$f_{lp}(n)$称为$f(n)$的近似，滤波器$h_1(n)$是一个高通滤波器，其输出子带$f_{hp}(n)$称为$f(n)$的高频部分或细节部分，综合滤波器组$g_0(n),g_1(n)$将两个子带$f_{lp}(n),f_{hp}(n)$合并产生$\hat{f}(n)$，子带编码的目的就是选择$h_0(n),h_1(n),g_0(n),g_1(n)$以便$\hat{f}(n)=f(n)$，也就是子带编码和解码系统的输入和输出是相同的，滤波器满足：
$$g_0(n)=(-1{)}^n{h}_1(n),g_1(n)=(-1{)}^{n+1}{h}_0(n)$$
或：
$$g_0(n)=(-1{)}^{n+1}{h}_1(n),g_1(n)=(-1{)}^n{h}_0(n)$$
上式中的滤波器被看成交叉调制，可以看到满足双正交条件：
< h i ( 2 n − k ) , g j ( k ) > = δ ( i − j ) δ ( n ) , i , j = { 0 , 1 } \left<h_i(2n - k),g_j(k)\right> = \delta(i - j)\delta(n),i,j = \{0,1\} ⟨hi​(2n−k),gj​(k)⟩=δ(i−j)δ(n),i,j={0,1}
$⟨h_i(2n-k),g_j(k)⟩$表示内积，当$i\ne j$时内积为0，当$i=j$时内积为单位离散冲激函数$\delta (n)$，正交滤波器满足一下两个条件：
g 1 ( n ) = ( − 1 ) n g 0 ( K e v e n − 1 − n ) h i ( n ) = g i ( K e v e n − 1 − n ) , i { 0 , 1 } g_1(n) = (-1)^ng_0(K_{even} - 1 - n) \\ h_i(n) = g_i(K_{even} - 1 - n),i \{0,1\} g1​(n)=(−1)ng0​(Keven​−1−n)hi​(n)=gi​(Keven​−1−n),i{0,1}
可以看到正交滤波器可以围绕单一滤波器的冲激响应来开发，称为原型，其余的滤波器可以通过冲激响应来计算，而双正交滤波器需要两个原型；
二维的子带编码可以由一维的导出，先垂直后水平：最后的输出从上到下分别为输入图像的近似、垂直细节、水平细节、对角线细节子带

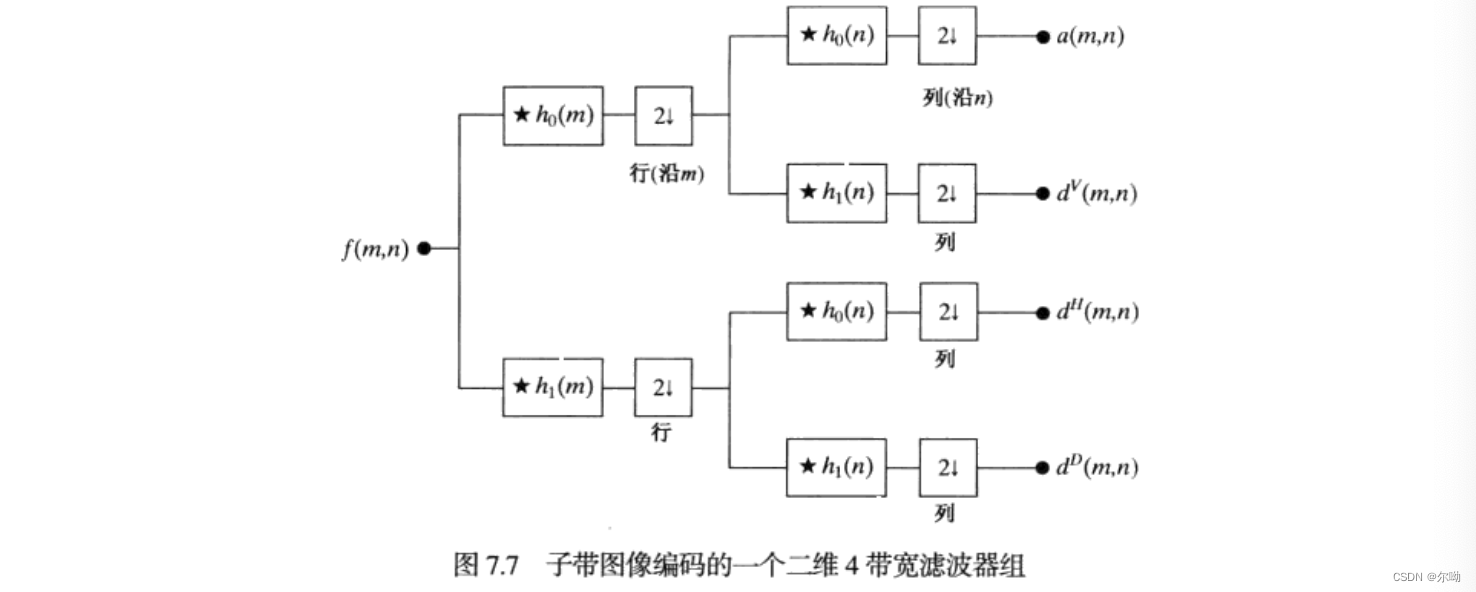
哈尔变换

哈尔变换用如下矩阵形式表示：
$$T=HF{H}^T$$
其中$F$是$N\times N$的图像矩阵，$H$是一个$N\times N$的哈尔变换矩阵，是非对称的，包含哈尔基函数$h_k(z)$，其中$z\in [0,1],k=0,1,2,\cdots ,N-1,N=2^n$，为了生成矩阵$H$，定义整数$k=2^p+q-1,0\le p\le n-1$，当$p=0$时$q=0$或$1$，当$p\ne 0$时，$1\le q\le 2^p$，哈尔基函数为：
$$\begin{gathered} h_0(z)=h_{00}(z)=\frac{1}{\sqrt{N}},z\in [0,1] \\ {h}_k(z)=h_{pq}(z)=\frac{1}{\sqrt{N}}\{\begin{array}{ll}{2}^{\frac{p}{2}}& (q-1)/2^p\le z<(q-0.5)/2^p\\ -2^{\frac{p}{2}}& (q-0.5)/2^p\le z<q/2^p\\ 0& otherwise,z\in [0,1]\end{array} \end{gathered}$$
$N\times N$哈尔变换矩阵的第$i$行包含了元素$h_i(z),z=\frac{0}{N},\frac{1}{N}\frac{2}{N},\cdots ,\frac{N-1}{N}$
$H_2$的行可用于定义一个2抽头完美重建滤波器组$h_0(n),h_1(n)$

多分辨率展开

信号或函数$f(x)$通常可以被很好的分解为一系列展开函数的线性组合：
$$f(x)=\sum _k{\alpha }_k{\phi }_k(x)$$
其中$k$是有限和或无限和的整数下标，${\alpha }_k$是具有实数值的展开系数，${\phi }_k(x)$是具有实数值的展开函数，如果展开是唯一的，也就是对于任何给定的$c$只有一组${\alpha }_k$与之对应，那么${\phi }_k(x)$就称为基函数，可展开的函数形成了一个函数空间，称为展开集合的闭合跨度，表示为：
V = S p a n k { φ k ( x ) } ‾ V = \overline{\mathop{Span}\limits_k\{\varphi_k(x)\}} V=kSpan​{φk​(x)}​
$f(x)\in V$的意思是$f(x)$属于闭合跨度，并可写成$f(x)={\sum }_k{\alpha }_k{\phi }_k(x)$的形式，对于任意的函数集合$V$，都有一个对偶函数集合 { φ ~ k ( x ) } \{\tilde\varphi_k(x)\} {φ~​k​(x)}，这个用来计算$f(x)={\sum }_k{\alpha }_k{\phi }_k(x)$的系数${\alpha }_k$，这些系数是通过计算对偶函数${\tilde{\phi }}_k(x)$和函数$f(x)$的内积得到的：
$${\alpha }_k=⟨{\tilde{\phi }}_k(x),f(x)⟩=\int {\tilde{\phi }}_k^{\ast }(x)f(x)dx$$
其中$\ast$表示复共轭操作，该计算假定是三种可能形式中的一种：

• 如果展开函数构成了$V$的一个正交基，即：
  $$⟨{\phi }_j(x),{\phi }_k(x)⟩={\delta }_{jk}=\{\begin{array}{ll}0& j\ne k\\ 1& j=k\end{array}$$
  则该基与它的对偶基相等${\phi }_k(x)={\tilde{\phi }}_k(x)$，则求系数操作变为：
  $${\alpha }_k=⟨{\phi }_k(x),f(x)⟩$$
• 展开函数本身不正交，但却是$V$的一个正交基：
  $$⟨{\phi }_j(x),{\phi }_k(x)⟩=0,j\ne k$$
  且基函数及其对偶称为双正交函数：
  $$⟨{\phi }_j(x),{\tilde{\phi }}_k(x)⟩={\delta }_{jk}=\{\begin{array}{ll}0& j\ne k\\ 1& j=k\end{array}$$
• 如果展开集合不是$V$的一个基，但是支持$f(x)={\sum }_k{\alpha }_k{\phi }_k(x)$的展开，那么它就是一个跨度集合，在该跨度集合中，任何$f(x)\in V$都有一个以上$a_k$的集合，展开函数及其对偶可以说是超完备的或冗余的，形成了一个框架，对于某些$A>0,B<\infty$以及所有的$f(x)\in V$有：
  $$A||f(x)|{|}^2\le \sum _k|⟨{\phi }_k(x),f(x)⟩{|}^2\le B||f(x)|{|}^2$$

尺度函数

集合 { φ j , k ( x ) } \{\varphi_{j,k}(x)\} {φj,k​(x)}表示整数平移、实数二值函数、平方可积函数$\phi (x)$组成的展开函数集合：
$${\phi }_{j,k}(x)=2^{\frac{j}{2}}\phi (2^{j}x-k)$$
其中$j,z\in Z,\phi (x)\in L^2(R),j$决定${\phi }_{j,k}(x)$的宽度，$j$越大，宽度越窄，分辨率越高，$k$决定${\phi }_{j,k}(x)$沿$x$轴的位置，前面的系数控制函数的幅度，${\phi }_{j,k}(x)$的形状随$j$发生改变，所以$\phi (x)$称为尺度函数，假设将$j$限定为$j_0$，得到原函数空间的一个子集，即子空间：
V j 0 = S p a n k { φ j 0 , k ( x ) } ‾ V_{j_0} = \overline{\mathop{Span}\limits_k\left\{\varphi_{j_0,k}(x)\right\}} Vj0​​=kSpan​{φj0​,k​(x)}​
假设$f(x)\in V_{j_0}$：
$$f(x)=\sum _k{\alpha }_k{\phi }_{j_0,k}(x)$$
更一般的，对于任何$j$，我们将$k$上跨越的子空间表示为：
V j = S p a n k { φ j , k ( x ) } ‾ V_j = \overline{\mathop{Span}\limits_k\left\{\varphi_{j,k}(x)\right\}} Vj​=kSpan​{φj,k​(x)}​
如果$f(x)$是$V_0$的元素，那么它也是$V_1$的元素，因为$j$越大，函数越窄，分辨率越高，所有的$V_0$展开函数都包含在$V_1$中，$V_0$是$V_1$的一个子空间，$V_0$的展开函数可以用$V_1$的展开函数表示，例如假设尺度函数为单位高度，单位宽度的尺度函数Haar：
$$\phi (x)=\{\begin{array}{ll}1& 0\le x<1\\ 0& otherwise\end{array}$$
那么可以计算：
$$\begin{array}{rl}{\phi }_{0,0}(x)& =\phi (x)\\ {\phi }_{0,1}(x)& =\phi (x-1)\\ {\phi }_{1,0}(x)& =\sqrt{2}\phi (2x)\\ {\phi }_{1,1}(x)& =\sqrt{2}\phi (2x-1)\end{array}$$
那么$V_0$就是${\phi }_{0,0}(x),{\phi }_{0,1}(x),\cdots$组成的函数空间，$V_1$同理，简单尺度函数遵循多分辨率分析的4个基本要求如下：

• MRA要求1：尺度函数对其整数平移是正交的，如上面的Haar哈尔函数就是
• MRA要求2：低尺度的尺度函数跨越子空间嵌套在高尺度跨越的子空间内，也就是包含高分辨率函数的子空间必须同时包含所有的低分辨率函数：
  $$V_{-\infty }\subset \cdots \subset V_{-1}\subset V_0\subset V_1\subset V_2\subset \cdots \subset V_{\infty }$$
  这些子空间还满足直观条件，即如果$f(x)\in V_j$，那么$f(2x)\in V_{j+1}$
• MRA要求3：唯一对所有的$V_j$通用的函数是$f(x)=0$，最粗糙的展开函数 V − ∞ = { 0 } V_{-\infty} = \{0\} V−∞​={0}
• 任何函数都可以以任意精度表示，虽然不能以任意粗糙的分辨率来展开一个特定的$f(x)$，但所有可度量的、平方可积的函数都可以由尺度函数在$j\to \infty$的限制下表示，即：
  V ∞ = { L 2 ( R ) } V_\infty = \{L^2(R)\} V∞​={L2(R)}
  在这些条件下，子空间$V_j$的展开函数可以表述为子空间$V_{j+1}$的展开函数的加权和：
  $${\phi }_{j,k}(x)=\sum _n{\alpha }_n{\phi }_{j+1,n}(x)$$
  得到：
  $${\phi }_{j,k}(x)=\sum _n{h}_{\phi }(n)2^{\frac{j+1}{2}}\phi (2^{j+1}x-n)$$
  将$j,k$置为0，且$\phi (x)={\phi }_{0,0}(x)$，得到：
  $$\phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n)$$
  该递归等式中的系数$h_{\phi }(n)$称为尺度函数系数，$h_{\phi }$称尺度向量，上式是多分辨率分析的基础，称为改进等式、MRA等式或扩张等式，表明任意子空间的展开函数都可以由其本身的双倍分辨率副本来建立，即来自相邻较高分辨率空间的展开函数

小波函数

给定满足MRA要求的尺度函数，定义小波函数$\psi (x)$，首先定义小波集合 { ψ j , k ( x ) } \{\psi_{j,k}(x)\} {ψj,k​(x)}
$${\psi }_{j,k}(x)=2^{\frac{j}{2}}\psi (2^{j}x-k)$$
使用尺度函数：
W j = S p a n k { ψ j , k ( x ) } ‾ W_j = \overline{\mathop{Span}\limits_k\{\psi_{j,k}(x)\}} Wj​=kSpan​{ψj,k​(x)}​
如果$f(x)\in W_j$，有：
$$f(x)=\sum _k{\alpha }_k{\psi }_{j,k}(x)$$
定义：
$$V_{j+1}=V_j\oplus W_j$$
其中$\oplus$表示空间的并集，$V_{j+1}$中$V_j$的正交补集为$W_j$，且$V_j$中的所有成员对于$W_j$中的所有成员都正交：
$$⟨{\phi }_{j,k}(x),{\psi }_{j,l}(x)⟩=0$$
对所有$j,k,l\in Z$都成立
可以将所有可度量的，平方可积的函数空间表示为：
$$\begin{gathered} L^2(R)=V_0\oplus W_0\oplus W_1\oplus \cdots \\ {L}^2(R)=\cdots \oplus W_{-2}\oplus W_{-1}\oplus W_0\oplus W_1\oplus W_2\oplus \cdots \end{gathered}$$
可以推广到：
$$L^2(R)=V_{j_0}\oplus W_{j_0}\oplus W_{j_0+1}\oplus \cdots$$
由于小波空间存在于由相邻较高分辨率尺度函数跨越的空间中，所以任何小波函数可以表示为平移后的双倍分辨率尺度函数的加权和：注意后面是$\phi$而不是$\psi$！
$$\psi (x)=\sum _n{h}_{\psi }(n)\sqrt{2}\phi (2x-n)$$
其中$h_{\psi }(n)$称为小波函数系数，$h_{\psi }$为小波变量，其中$h_{\psi }(n),h_{\phi }(n)$的关系：
$$h_{\psi }(n)=(-1{)}^n{h}_{\phi }(1-n)$$