机器学习中的数学：（一）线性代数

本博客是对MATHEMATICS FOR MACHINE LEARNING的学习笔记，因为是全英文的书籍，所以在每节之后都会收集一些相关的术语，然后笔记中也可能会加入一些英文。当然，作为一个个人笔记，我会加入一些自己的理解，这些理解可能会因为自己的能力有限而不够深入并且有较大的局限性，但是，我会不断复习自己的笔记，并不断更新自己的理解。这正如孔子所说的：温故而知新，可以为师矣。
ps:想要这本书的电子版可以私信我。
pps:我认为大脑能更加轻易地记忆图片，图片会比文字更好理解，所以我会尽可能的多加一些图片在笔记中。

---

前言

这部分讲解了书籍的组成，对书籍的各个章节做了一些简要的介绍，并探讨了书籍的学习方式。
总的来说，这本书分为两个部分，上半部分是将一些数学基础包含线性代数(Linear Algebra)、分析几何(Analytic Geometry)、矩阵分解(Matrix Decomposition)和概率论(Probability Theoty)，第二部分是讲解机器学习的四大支柱(pillars)技术。

文中提及了两种学习模式：自顶向下和自底向上。两种方法都有各自的优势和劣势。我的学习模式类似于自底向上，先完成数学理论知识的学习然后再将学过的数学知识用于机器学习理论的学习中，这个过程帮助我进一步强化学过的数学知识，就当一个复习的过程。

---

一些题外话：在我接触机器学习的一些理论的时候，我发现这些理论在一定程度上与人类自己的认知过程有一定的相似之处，所以，我觉得将用这些理论去思考自己的学习过程，并且用自己的学习过程去理解这些理论都是可以帮助自己更好地提升对“学习”的理解。

Linear Algebra

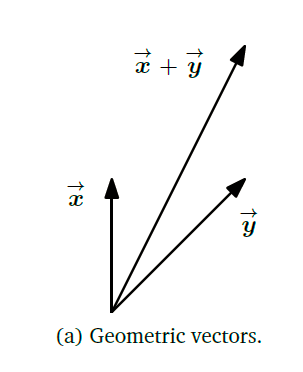
Linear algebra is the study of vectors and certain algebra rules to manipulate vectors.

线性代数就是向量+对向量的操作。而向量就是一个数据集，对应着具体事物的不同属性。放到空间中，向量就是方向+数量（direction and magnitude）。我们需要弄清楚的是，在不同的情形下，对向量的运算会对这些数字所对应的属性产生什么变化。例如两个向量的相加，可会将原先的向量在长度和方向上的变化。

前半部分介绍线性代数的基础知识，我只记录自己不熟悉的部分和大致内容。 ## Foundations

逆

公式法：$A^{-1}=\frac{A^{\ast }}{|A|}$
解方程：$AX=I_n$ 求解 $[A|I_n]->[I_n|A^{-1}]$

解方程

通解 = 非齐次特解 + 非齐次通解

The Minus-1 Trick（快速求解齐次方程通解）
在行阶梯矩阵中，添加单位行向量，非零元素对应非主元元素位置，此时原先非主元元素所在的列向量就是通解向量。
原矩阵：
$$A=\left[\begin{array}{ccccc}1& 3& 0& 0& 3\\ 0& 0& 1& 0& 9\\ 0& 0& 0& 1& -4\end{array}\right]$$

增广矩阵：

通解：
$$\left\{x\in {\mathbb{R}}^5:x={\lambda }_1\left[\begin{array}{c}3\\ -1\\ 0\\ 0\\ 0\end{array}\right]+{\lambda }_2\left[\begin{array}{c}3\\ 0\\ 9\\ -1\\ -1\end{array}\right],{\lambda }_1,{\lambda }_2\in \mathbb{R}\right\}$$

计算线性方程$Ax=b$

如果A是方阵并且可逆，可以通过逆直接求出来：$x=A^{-1}b$
推广至一般矩阵，需要用到伪逆（Moore-Penrose pseudo-inverse）：
$$Ax=b\iff A^{T}Ax=A^{T}b\iff x=(A^{T}A{)}^{-1}{A}^{T}b$$
$(A^{T}A{)}^{-1}{A}^T$:Moore-Penrose pseudo-inverse
但是这方法需要大量的矩阵运算，可能会在计算精度上有损失

这个逆是泛化的矩阵的逆，标记为$A^{+}$。这里是巧妙地规避了对非方阵矩阵的求逆，而不改变原先的属性。对于一个任意矩阵$A$, $(A^{\top }A{)}^{-1}{A}^{\top }=A^{-1}(A^{\top }{)}^{-1}{A}^{\top }=A^{-1}$
它可以用于奇异值分解。

还可以使用高斯消元法，这个方法虽然广泛使用，但是需要立方数量级的算数运算，计算较大。

还有一种迭代方法（Iterative method）:
$$x^{(k+1)}=C{x}^{(k)}+d$$
在迭代的过程中，残差（residual error）：$\Vert x^{(k+1)}-x_{\ast }\Vert$,不断减小，最终向$x_{\ast }$收敛

Hadamard product

矩阵对应位置元素相乘。

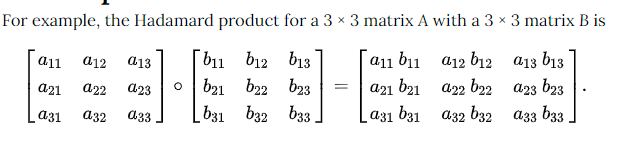
向量空间（Vector Space）

Group: Object + Operations

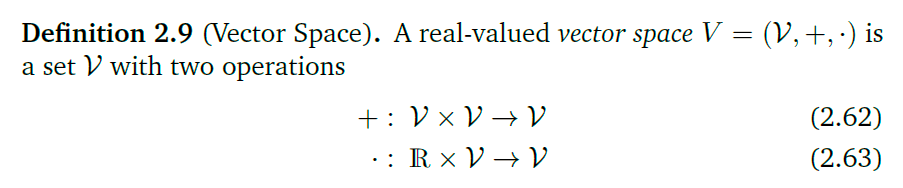
我对这个定义的理解是，一个向量经过外积和向量积所能表示的所有的向量一个向量经过线性组合和数乘得到的所有的向量，这些所有的向量组成的空间就是这个向量的向量空间。（张成空间：两向量的全部线性组合构成的向量空间）

将一个向量看成向量空间中的一个点，这个点乘以所有的实数得到的所有的向量组成一条直线，这条直线就是这个向量张成的向量空间($\mathbb{R}$)。它与另外一个不平行的直线的所有的线性组合会得到一个平面，这就是两个向量张成的二维空间(${\mathbb{R}}^2$)

对这个定义的理解还需要补充

线性的严格定义：$$\begin{gathered} L(c\vec{v})=cL(\vec{v}) \\ L(\vec{v}+\vec{w})=L(\vec{v})+L(\vec{w}) \end{gathered}$$
将L当成一种变换，对向量进行数量积之后进行变换和变换之后对向量进行数量积的结果是一致的。
拥有这种性质的算子很多， 例如求导：$\frac{d}{dx}(4x^2)=4\times \frac{d}{dx}(x^2)$

向量子空间（Vector subspace）

向量子空间需要满足加法封闭性和数乘封闭性。也就是向量子空间中的向量在经过任意的数乘或线性组合之后得到的向量仍在这个子空间中。

判断是否为向量子空间，需要满足封闭性，也就是经过对应的运算之后，向量仍旧属于原先的向量空间。

例：

the closure property is violated;因为向量空间需要满足加法封闭性，也就是说在这个空间中向量之间的运算之后的向量，需要还在这个空间中，上面这个空间显然不满足这个条件。

线性无关

矩阵线性无关就是说每一个都是相互独立的，不能由其他向量表示出来。表现在公式上：
$$\sum _{i=1}^k{\lambda }_i{x}_i=0$$
当且仅当上式中$\lambda$为0时，成立，说明向量$x_i$线性无关。
空间上理解就是，每一个向量代表一个维度，少了其中一个就会导致降维,这也就是秩 。当有向量对维度的没有贡献的时候，就说这个向量是线性相关的。

Basis and Rank

Generating set and basis

生成集就是能够表示向量空间的向量集合，这也就是说生成集中向量通过线性组合等方式可以表示向量空间中的所有的向量（能通过数乘和线性组合表示整个向量空间的向量）。而生成集所形成的向量空间称为张成空间（span）
V = ( V , + , ⋅ ) , A = { x 1 , x 2 , . . . . , x k } ⊆ V V = (\mathcal{V},+,\cdot ), \mathcal{A} = \{x_1,x_2,....,x_k\} \subseteq \mathcal{V} V=(V,+,⋅),A={x1​,x2​,....,xk​}⊆V
对于任意$v\in \mathcal{V}$能被$\mathcal{A}$线性表出，则称$\mathcal{A}$是$\mathcal{V}$的一个生成集。$\mathcal{A}$所能线性表示的所有向量组成的空间成为$\mathcal{A}$的张成空间，表示为$V=span[\mathcal{A}]$
生成集中最小的集合成为基（basis）

下图展示了关于这个概念的等价描述：

现在有一个问题，是不是任意n个n维的线性无关的向量都是n维空间的一个生成集呢？
并不是，因为这个n个向量可能只能形成n维空间的一个子空间，并不能表示该空间当中所有的向量，所以并不是这个空间的一个生成集。

How can you describe it in graph?存疑

当向量组是线性无关的时候，每一个向量代表一个维度，将向量空间的维度表示为$dim(\mathcal{V})$,如果，$\mathcal{U}\subseteq \mathcal{V}$是$\mathcal{V}$的一个子空间，则有：
$$dim(\mathcal{V})\ge dim(\mathcal{U}),ifandonlyif\mathcal{V}=\mathcal{U}\Rightarrow dim(\mathcal{V})=dim(\mathcal{U})$$

Rank

秩可以表示为向量组中线性无关的列向量的个数，也就是向量组的向量空间的维度。其他还有一些相关的性质：

线性映射（Linear Mappings/vector space homomorphism/ linear transformation）

对于向量空间$V$和$W$的线性映射$\Phi :V\to W$有如下定义:
$$\forall \mathbf{x},\mathbf{y}\in \mathbf{V}\forall \lambda ,\psi \in \mathbb{R}:\mathbf{\Phi }(\lambda \mathbf{x}+\psi \mathbf{y})=\lambda \mathbf{\Phi }(\mathbf{x})+\psi \mathbf{\Phi }(\mathbf{y})$$

这样的映射关系可以用矩阵表示：
$$\Phi (\lambda x+\psi y)=[\lambda \psi ]\left[\begin{array}{c}{\Phi }_{(x)}\\ {\Phi }_{(y)}\end{array}\right]$$
下面是几个特殊的映射：

满射就是y的所有元素都可以由x中的元素映射得来

逆映射：对于映射$\Phi :\mathcal{W}\to \mathcal{V}$有 ：$\Phi (x)\circ \Psi =x$,则$\Psi$为$\Phi (x)$的逆映射，表示为${\Phi }^{-1}(x)$

一些特殊的线性映射：

有疑问？需要理解一下

这里是解释为什么复数可以表示维二维坐标的形式，因为我们可以使用双线性映射将二维坐标数组转化成复数空间中的加法形式(利用一个映射就可以转换了)

同构：抓取一个数学对象最本质的信息（比如上面例子里的加法和乘法结构），而忽略其他没那么重要的信息（比如进制），然后把具有相同“本质信息”的对象视为一体。（例如一个对象中包含三个个体，那么所有包含三个个体的对象都可以说是同构的，因为他们都有3这个特征）
同态：它是在两个本质不一定相同的数学对象之间建立联系（两不一定完全一致的对象是更大结构的一部分）

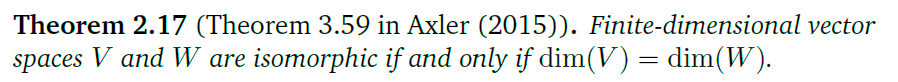
这个定理表明拥有相同维度的向量空间在一定程度上是相同的。
${\mathbb{R}}^{n\times m}\&{\mathbb{R}}^{nm}$：一个是n×m矩阵一个是nm维度向量，二者的维度是一样的，而且他们之间能够通过一种线性映射（双映射）相互转换.

如何在图形上理解n×m矩阵和nm维度向量是同形的？

线性映射的矩阵表示

对于一个元组$\mathbf{B}=({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_n)$中,各个向量的位置是不能交换的，也就是说这些向量的位置也是作为这个元组的一个信息，这样的元组称为有序基(ordered basis)

在此书中，用$\mathbf{B}=({\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_n)$表示有序基； B = { x 1 , x 2 , . . . , x n } \bold B = \{\bold x_1,\bold x_2,...,\bold x_n\} B={x1​,x2​,...,xn​}表示（无序）基； $\mathbf{B}=[{\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_n]$表示一个矩阵。

所以对于一个有序基 B = { b 1 , b 2 . . . b n } ⊆ R n \bold B = \{\bold {b_1},\bold {b_2}...\bold {b_n}\} \subseteq \mathbb{R}^n B={b1​,b2​...bn​}⊆Rn,对于${\mathbb{R}}^n$中的所有向量，都可以由$\mathbf{B}$唯一线性表出。即：
$$x\in {\mathbb{R}}^n,x={\alpha }_1{\mathbf{b}}_1+{\alpha }_2{\mathbf{b}}_2+....+{\alpha }_n{\mathbf{b}}_{\mathbf{n}}$$
$\alpha$组成的向量就是向量$\mathbf{x}$在向量空间中以$\mathbf{B}$为基向量的坐标。

向量的坐标依赖于基向量，在不同的基向量中的坐标不同。

想要完成有一对基向量组成的向量空间中的向量映射到另一对基向量组成的向量空间中的向量，这可以使用一个矩阵完成，这样的矩阵被称为变换矩阵（Transformation Matrix）

一个向量空间中的向量可以表示为：$\mathbf{a}=x{\mathbf{e}}_1+y{\mathbf{e}}_2$表示为矩阵形式就是
$$\mathbf{a}=[{\mathbf{e}}_1{\mathbf{e}}_2]\left[\begin{array}{c}x\\ y\end{array}\right]$$
假设$e_1、e_2$是${\mathbb{R}}^2$向量空间的基向量，所以上式可以表示为：
$$\mathbf{a}=\left[\begin{array}{c}10\\ 01\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
这一个单位矩阵也可以看成一种变换，但是是一种原封不动的变换，现在假设有一个变换矩阵$\mathbf{b}=\left[\begin{array}{c}20\\ 01\end{array}\right]$。所以，$\mathbf{a}\cdot \mathbf{b}$就相当于对原先的向量空间y轴上的延伸操作。这也是一种对向量的线性变换

基变换(Basis Change)

这部分探寻向量空间发生变化之后，变换矩阵的情况。有几种情形，首先是在同一个向量空间中的基变换，这种变换也成为恒等映射（identity mapping）例如：$\Psi =i{d}_V$表示在向量空间V中的恒等映射。
还有一种向量空间发生变化的情况。在下图中，蓝色的字母代表有序基，箭头上的希腊字母代表着对应的变换矩阵

我们能够通过原先的变换矩阵得到${\tilde{A}}_{\Phi }$:
$${\Phi }_{\tilde{C}\tilde{B}}={\Xi }_{\tilde{C}C}\circ {\Phi }_{CB}\circ {\Psi }_{B\tilde{B}}={\Xi }_{C\tilde{C}}^{-1}\circ {\Phi }_{CB}\circ {\Psi }_{B\tilde{B}}$$
这也就是说一个基的多个变换可以等价于某一个单一的变换。

对上式的一个粗略的推导：

等价与相似：

正则矩阵（Regular Matrix）: 我们常见的实数矩阵和复数矩阵中，正则矩阵=可逆矩阵

像集与核（Image and Kernel）

零空间就是一个向量空间中的向量，经过映射$\Phi$之后，变成零向量的所有向量组成的向量空间，e.g: $\mathbf{A}\mathbf{x}=0$的解就是A的一个零空间。因为$\Phi (0_V)=\Phi (0_W)$总是成立，所以零空间不会是空的。零空间也可以用于确定列向量之间是否是线性相关的。

如何从映射的角度，理解这个线性相关？

假设存在这样的一个映射使得，$V$中的一个子空间经过线性映射之后变成了一个0空间，说明这个过程发生了降维，零空间就是在转换之后损失掉的维度，而变换矩阵所在向量空间的维度，影响变换之后的向量空间的维度，而变换矩阵的列向量就是描述这样的维度的量，所对应的就是列空间

像集就是映射之后所对应的向量组成的向量空间。e.g:$\mathbf{A}\mathbf{x}=\mathbf{b}$

从上图知：$\Phi$的核空间是$V$的一个向量子空间，而其像域是$W$的一个向量子空间。所以，像域是$V$在映射之后在$W$的子空间，零空间是$V$中映射之后变成$W$中的零的一个向量子空间。

列空间
变换矩阵列向量所形成的张成空间，就是列空间

秩－零化度定理

思考这个等式为什么会成立？

其实就是在变换过程中损失的维度和变换后的维度之和等于变换之前的向量空间的维度。而这样的损失是由于变换矩阵导致，这也就是说变换之后的维度等于变换矩阵的维度，这也就是为什么$\Phi$的像域是A的列空间了。
上面那个结论其实说的就是在变换之后丢失了一些维度，所以，零空间至少是一维的，在这个空间上的向量又是无限多的，所以就是有无穷解了。

仿射空间（Affine Spaces）

仿射子空间

实际上就是一个不经过原点的子空间，描述为一个子空间加上一些偏置，使得这个空间不经过原点。例如。三维空间的一个仿射子空间就是一个不经过原点的点、线或者面。

想想这段话的含义

想清楚仿射空间与线性非齐次方程之间的关系。

一个实例：

向量可以用向量空间的有序基线性表示，同样的仿射空间中的向量可以由同样的方式表示，只需要在每个向量中加上支持点（support point）即可

仿射映射

与线性映射类似，仿射映射只不过是在线性映射之后加上一个偏置量（支撑点）。