文章目录
- 单变量微分(Differentiation of Univariate Functions)
- 偏导数和梯度(Partial Differentiation and Gradients)
- 向量值函数的梯度(Gradients of Vector-Valued Functions)
- 矩阵梯度(Gradients of Matrices)
- 计算梯度时有用的恒等式(Useful Identities for Computing Gradients)
- 反向传播和自动微分(Backpropagation and Automatic Differentiation)
- 高阶偏导数(Higher-Order Derivatives)
- 线性化和多元泰勒级数(Linearization and Multivariate Taylor Series)
- 补充

单变量微分(Differentiation of Univariate Functions)
定义:差商形式


正式定义:
割线在极限情况下变成切线

多项式导数的推导:
d f d x = lim h → 0 f ( x + h ) − f ( x ) h = lim h → 0 ( x + h ) n − x n h = lim h → 0 ∑ i = 0 n ( n i ) x n − i h i − x n h . \begin{aligned} \frac{\mathrm{d} f}{\mathrm{~d} x} &=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\\ &=\lim _{h \rightarrow 0} \frac{(x+h)^{n}-x^{n}}{h} \\ &=\lim _{h \rightarrow 0} \frac{\sum_{i=0}^{n}\left(\begin{array}{l} n \\ i \end{array}\right) x^{n-i} h^{i}-x^{n}}{h} . \end{aligned} dxdf=h→0limhf(x+h)−f(x)=h→0limh(x+h)n−xn=h→0limh∑i=0n(ni)xn−ihi−xn.
由于 x n = ( n 0 ) x n − 0 h 0 x^n=\left(\begin{array}{l}n \\ 0 \end{array}\right)x^{n-0}h^0 xn=(n0)xn−0h0所以:
d f d x = lim h → 0 ∑ i = 1 n ( n i ) x n − i h i h = lim h → 0 ∑ i = 1 n ( n i ) x n − i h i − 1 = lim h → 0 ( n 1 ) x n − 1 + ∑ i = 2 n ( n i ) x n − i h i − 1 ⏟ → 0 as h → 0 = n ! 1 ! ( n − 1 ) ! x n − 1 = n x n − 1 . \begin{aligned} \frac{\mathrm{d} f}{\mathrm{~d} x} &=\lim _{h \rightarrow 0} \frac{\sum_{i=1}^{n}\left(\begin{array}{l} n \\ i \end{array}\right) x^{n-i} h^{i}}{h} \\ &=\lim _{h \rightarrow 0} \sum_{i=1}^{n}\left(\begin{array}{c} n \\ i \end{array}\right) x^{n-i} h^{i-1} \\ &=\lim _{h \rightarrow 0}\left(\begin{array}{l} n \\ 1 \end{array}\right) x^{n-1}+\underbrace{\sum_{i=2}^{n}\left(\begin{array}{l} n \\ i \end{array}\right) x^{n-i} h^{i-1}}_{\rightarrow 0 \text { as } h \rightarrow 0} \\ &=\frac{n !}{1 !(n-1) !} x^{n-1}=n x^{n-1} . \end{aligned} dxdf=h→0limh∑i=1n(ni)xn−ihi=h→0limi=1∑n(ni)xn−ihi−1=h→0lim(n1)xn−1+→0 as h→0 i=2∑n(ni)xn−ihi−1=1!(n−1)!n!xn−1=nxn−1.
其中的 ( n i ) \left(\begin{array}{l} n \\ i \end{array}\right) (ni)是组合数 C n i C^i_n Cni
泰勒级数
泰勒多项式:

对于
f
∈
C
∞
,
f
:
R
→
R
,
f
f\in\mathcal C^{\infty}, f:\mathbb R \rightarrow \mathcal R,f
f∈C∞,f:R→R,f在
x
0
x_0
x0的泰勒级数为:(
f
∈
C
∞
f\in\mathcal C^{\infty}
f∈C∞表示
f
f
f无穷多项都是是连续可微的,?)
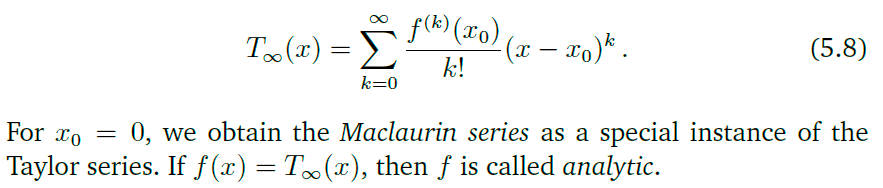
当
x
0
=
0
x_0=0
x0=0时.称为麦克劳林级数(Maclaurin series)
泰勒多项式表示对函数的一种近似,多项式的项越多,与原先的函数就越接近.下图中,
T
i
T_i
Ti表示
f
f
f的
i
i
i项展开。

三角函数的泰勒展开:
cos ( x ) = ∑ k = 0 ∞ ( − 1 ) k 1 ( 2 k ) ! x 2 k , sin ( x ) = ∑ k = 0 ∞ ( − 1 ) k 1 ( 2 k + 1 ) ! x 2 k + 1 . \begin{aligned} \cos (x) &=\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k) !} x^{2 k}, \\ \sin (x) &=\sum_{k=0}^{\infty}(-1)^{k} \frac{1}{(2 k+1) !} x^{2 k+1} . \end{aligned} cos(x)sin(x)=k=0∑∞(−1)k(2k)!1x2k,=k=0∑∞(−1)k(2k+1)!1x2k+1.
泰勒级数实际上是一种特殊的幂级数:
f ( x ) = ∑ k = 0 ∞ a k ( x − c ) k , 幂 级 数 f(x)=\sum^\infty_{k=0}a_k(x-c)^k,\quad 幂级数 f(x)=k=0∑∞ak(x−c)k,幂级数
一些求导法则:

偏导数和梯度(Partial Differentiation and Gradients)
偏导数定义:
∂
f
∂
x
1
=
lim
h
→
0
f
(
x
1
+
h
,
x
2
,
…
,
x
n
)
−
f
(
x
)
h
⋮
∂
f
∂
x
n
=
lim
h
→
0
f
(
x
1
,
…
,
x
n
−
1
,
x
n
+
h
)
−
f
(
x
)
h
\begin{aligned} \frac{\partial f}{\partial x_{1}} &=\lim _{h \rightarrow 0} \frac{f\left(x_{1}+h, x_{2}, \ldots, x_{n}\right)-f(x)}{h} \\ & \vdots \\ \frac{\partial f}{\partial x_{n}} &=\lim _{h \rightarrow 0} \frac{f\left(x_{1}, \ldots, x_{n-1}, x_{n}+h\right)-f(\boldsymbol{x})}{h} \end{aligned}
∂x1∂f∂xn∂f=h→0limhf(x1+h,x2,…,xn)−f(x)⋮=h→0limhf(x1,…,xn−1,xn+h)−f(x)
可以将函数对所有变量的偏导数写成一个行向量:
∇
x
f
=
grad
f
=
d
f
d
x
=
[
∂
f
(
x
)
∂
x
1
∂
f
(
x
)
∂
x
2
⋯
∂
f
(
x
)
∂
x
n
]
∈
R
1
×
n
\nabla_{\boldsymbol{x}} f=\operatorname{grad} f=\frac{\mathrm{d} f}{\mathrm{~d} \boldsymbol{x}}=\left[\begin{array}{llll} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} & \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} & \cdots & \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right] \in \mathbb{R}^{1 \times n}
∇xf=gradf= dxdf=[∂x1∂f(x)∂x2∂f(x)⋯∂xn∂f(x)]∈R1×n
这个式子被称为
f
f
f的梯度或者雅可比矩阵(Jacobian)。
对于一个多变量函数的偏导数(
f
=
(
x
1
,
x
2
)
,
x
1
=
x
1
(
s
,
t
)
,
x
2
=
x
2
(
s
,
t
)
f=(x_1,x_2),x_1=x_1(s,t),x_2=x_2(s,t)
f=(x1,x2),x1=x1(s,t),x2=x2(s,t))可以写成矩阵乘法的形式:
d
f
d
(
s
,
t
)
=
∂
f
∂
x
∂
x
∂
(
s
,
t
)
=
[
∂
f
∂
x
1
∂
f
∂
x
2
]
⏟
=
∂
f
∂
x
[
∂
x
1
∂
s
∂
x
1
∂
t
∂
x
2
∂
s
∂
x
2
∂
t
]
⏟
=
∂
x
∂
(
s
,
t
)
.
\frac{\mathrm{d} f}{\mathrm{~d}(s, t)}=\frac{\partial f}{\partial \boldsymbol{x}} \frac{\partial \boldsymbol{x}}{\partial(s, t)}=\underbrace{\left[\frac{\partial f}{\partial x_{1}} \quad \frac{\partial f}{\partial x_{2}}\right]}_{=\frac{\partial f}{\partial \boldsymbol{x}}} \underbrace{\left[\begin{array}{cc} \frac{\partial x_{1}}{\partial s} & \frac{\partial x_{1}}{\partial t} \\ \frac{\partial x_{2}}{\partial s} & \frac{\partial x_{2}}{\partial t} \end{array}\right]}_{=\frac{\partial \boldsymbol{x}}{\partial(s, t)}} .
d(s,t)df=∂x∂f∂(s,t)∂x==∂x∂f
[∂x1∂f∂x2∂f]=∂(s,t)∂x
[∂s∂x1∂s∂x2∂t∂x1∂t∂x2].
为了检验梯度计算结果的正确行,可以采用梯度验证(Gradient checking)的方式进行检验:
这里用到了有限差分法(Finite difference method,FDM):FDM are one of the most common approaches to the numerical solution of PDE(partial differential equations), along with finite element methods.
就是将连续函数离散化。FDM的基本原理就是利用一个很小的数 ϵ ( 1 0 − 4 ) \epsilon(10^{-4}) ϵ(10−4),判断自变量在这个范围中变化时对应的函数值的变化情况是否与梯度相似。
d d θ J ( θ ) ≈ J ( θ + ϵ ) − J ( θ − ϵ ) 2 ϵ , ϵ → 0 \frac{d}{d\theta}J(\theta)\approx \frac{J(\theta + \epsilon)-J(\theta-\epsilon)}{2\epsilon}, \quad \epsilon\rightarrow 0 dθdJ(θ)≈2ϵJ(θ+ϵ)−J(θ−ϵ),ϵ→0
向量值函数的梯度(Gradients of Vector-Valued Functions)

这样,
f
\boldsymbol f
f就将原先的
x
∈
R
n
\boldsymbol x \in \mathbb R^n
x∈Rn映射成
R
m
\mathbb R^m
Rm,对于每一个
f
i
:
R
n
→
R
\boldsymbol f_i:\mathbb R^n\rightarrow\mathbb R
fi:Rn→R,也就是将原先的n维自变量映射成了一个实数。
所以:
∂
f
(
x
)
∂
x
i
=
[
∂
f
1
(
x
)
∂
x
i
⋮
∂
f
m
(
x
)
∂
x
i
]
∈
R
m
\frac{\partial\boldsymbol f(x)}{\partial x_i}=\left[\begin{array}{cc}\frac{\partial f_1(x)}{\partial x_i}\\\vdots\\ \frac{\partial f_m(x)}{\partial x_i} \end{array}\right]\in \mathbb R^m
∂xi∂f(x)=⎣⎢⎢⎡∂xi∂f1(x)⋮∂xi∂fm(x)⎦⎥⎥⎤∈Rm
而一个函数对一个列向量的映射,也就是之前提到梯度,可以写成:
∇
x
f
=
grad
f
=
d
f
d
x
=
[
∂
f
(
x
)
∂
x
1
∂
f
(
x
)
∂
x
2
⋯
∂
f
(
x
)
∂
x
n
]
∈
R
1
×
n
\nabla_{\boldsymbol{x}} f=\operatorname{grad} f=\frac{\mathrm{d} f}{\mathrm{~d} \boldsymbol{x}}=\left[\begin{array}{llll} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} & \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} & \cdots & \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right] \in \mathbb{R}^{1 \times n}
∇xf=gradf= dxdf=[∂x1∂f(x)∂x2∂f(x)⋯∂xn∂f(x)]∈R1×n
代入上式,得到向量值方程的一阶偏导数:
J
=
∇
x
f
=
d
f
(
x
)
d
x
=
[
∂
f
(
x
)
∂
x
1
⋯
∂
f
(
x
)
∂
x
n
]
=
[
∂
f
1
(
x
)
∂
x
1
⋯
∂
f
1
(
x
)
∂
x
n
⋮
⋮
∂
f
m
(
x
)
∂
x
1
⋯
∂
f
m
(
x
)
∂
x
n
]
x
=
[
x
1
⋮
x
n
]
,
J
(
i
,
j
)
=
∂
f
i
∂
x
j
.
\begin{aligned} J &=\nabla_{x} f=\frac{\mathrm{d} f(x)}{\mathrm{d} x}=\left[\begin{array}{ccc} \frac{\partial f(x)}{\partial x_{1}} & \cdots & \frac{\partial f(x)}{\partial x_{n}} \end{array}\right] \\ &=\left[\begin{array}{ccc} \frac{\partial f_{1}(x)}{\partial x_{1}} & \cdots & \frac{\partial f_{1}(x)}{\partial x_{n}} \\ \vdots & & \vdots \\ \frac{\partial f_{m}(x)}{\partial x_{1}} & \cdots & \frac{\partial f_{m}(x)}{\partial x_{n}} \end{array}\right] \\ x &=\left[\begin{array}{c} x_{1} \\ \vdots \\ x_{n} \end{array}\right], \quad J(i, j)=\frac{\partial f_{i}}{\partial x_{j}} . \end{aligned}
Jx=∇xf=dxdf(x)=[∂x1∂f(x)⋯∂xn∂f(x)]=⎣⎢⎢⎡∂x1∂f1(x)⋮∂x1∂fm(x)⋯⋯∂xn∂f1(x)⋮∂xn∂fm(x)⎦⎥⎥⎤=⎣⎢⎡x1⋮xn⎦⎥⎤,J(i,j)=∂xj∂fi.
f
:
R
n
→
R
m
\boldsymbol f:\mathbb R^n\rightarrow\mathbb R^m
f:Rn→Rm的一阶偏导数称为雅可比矩阵。
雅可比矩阵用于求解映射之后图形的比例因子(scaling factor)

想要找到比例因子,可以找出对应的变换矩阵,这个矩阵的行列式的绝对值就是面积变化的比例。但是这个适用于线性变换,当面对非线性变换的时候,需要采取另一种策略。
想要知道当
x
x
x变化的时候
f
(
x
)
f(x)
f(x)的变化情况,我们可以使用偏导数得到变化信息。所以,雅可比矩阵可以表示相对应的变换矩阵。
非线性的情况时,采用逼近的方式获得比例因子
向量和对应的映射所处的维度与偏导数的关系:
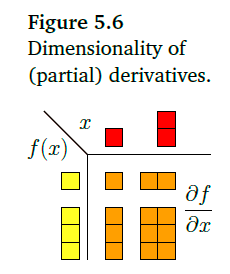
矩阵梯度(Gradients of Matrices)
矩阵的梯度的结果可能得到一个高维的矩阵,这种矩阵称为张量(Tensor)
两种计算矩阵梯度的方法:
一种是直接计算,最后将结果拼装起来,另一种是将矩阵变成一个向量,

d K d R ∈ R ( N × N ) × ( M × N ) \frac{d\boldsymbol K}{d\boldsymbol R}\in \mathbb R^{(N\times N)\times(M\times N)} dRdK∈R(N×N)×(M×N)
d K p q d R ∈ R 1 × ( M × N ) \frac {d K_{pq}}{d\boldsymbol R}\in \mathbb R^{1\times(M\times N)} dRdKpq∈R1×(M×N)
K p q = r p ⊤ r q = ∑ m = 1 M R m q R m p K_{pq}=r_p^\top r_q=\sum^M_{m=1}\boldsymbol R_{mq}\boldsymbol R_{mp} Kpq=rp⊤rq=m=1∑MRmqRmp
∂ K p q ∂ R i j = ∑ m = 1 M ∂ ∂ R i j R m p R m q = ∂ p q i j , ∂ ∂ p q i j = { R i q if j = p , p ≠ q R i p if j = q , p ≠ q 2 R i q if j = p , p = q 0 otherwise . \frac{\partial \boldsymbol K_{pq}}{\partial \boldsymbol R_{ij}}=\sum_{m=1}^M\frac{\partial}{\partial R_{ij}}R_{mp}R_{mq}=\partial_{pqij},\partial_{} \partial_{p q i j}=\left\{\begin{array}{ll} R_{i q} & \text { if } j=p, p \neq q \\ R_{i p} & \text { if } j=q, p \neq q \\ 2 R_{i q} & \text { if } j=p, p=q \\ 0 & \text { otherwise } \end{array} .\right. ∂Rij∂Kpq=m=1∑M∂Rij∂RmpRmq=∂pqij,∂∂pqij=⎩⎪⎪⎨⎪⎪⎧RiqRip2Riq0 if j=p,p=q if j=q,p=q if j=p,p=q otherwise .
计算梯度时有用的恒等式(Useful Identities for Computing Gradients)
∂ ∂ X f ( X ) ⊤ = ( ∂ f ( X ) ∂ X ) ⊤ ∂ ∂ X tr ( f ( X ) ) = tr ( ∂ f ( X ) ∂ X ) ∂ ∂ X det ( f ( X ) ) = det ( f ( X ) ) tr ( f ( X ) − 1 ∂ f ( X ) ∂ X ) ∂ ∂ X f ( X ) − 1 = − f ( X ) − 1 ∂ f ( X ) ∂ X f ( X ) − 1 ∂ a ⊤ X − 1 b ∂ X = − ( X − 1 ) ⊤ a b ⊤ ( X − 1 ) ⊤ ∂ x ⊤ a ∂ x = a ⊤ ∂ a ⊤ x ∂ x = a ⊤ ∂ a ⊤ X b ∂ X = a b ⊤ ∂ x ⊤ B x ∂ x = x ⊤ ( B + B ⊤ ) ∂ ∂ s ( x − A s ) ⊤ W ( x − A s ) = − 2 ( x − A s ) ⊤ W A for symmetric W ( 5.108 ) \begin{aligned} &\frac{\partial}{\partial \boldsymbol{X}} \boldsymbol{f} (\boldsymbol{X})^{\top}=\left(\frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}}\right)^{\top}\\ &\frac{\partial}{\partial \boldsymbol{X}} \operatorname{tr}(\boldsymbol{f}(\boldsymbol{X}))=\operatorname{tr}\left(\frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}}\right)\\ &\frac{\partial}{\partial \boldsymbol{X}} \operatorname{det}(\boldsymbol{f}(\boldsymbol{X}))=\operatorname{det}(\boldsymbol{f}(\boldsymbol{X})) \operatorname{tr}\left(\boldsymbol{f}(\boldsymbol{X})^{-1} \frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}}\right)\\ &\frac{\partial}{\partial \boldsymbol{X}} \boldsymbol{f}(\boldsymbol{X})^{-1}=-\boldsymbol{f}(\boldsymbol{X})^{-1} \frac{\partial \boldsymbol{f}(\boldsymbol{X})}{\partial \boldsymbol{X}} \boldsymbol{f}(\boldsymbol{X})^{-1}\\ &\frac{\partial \boldsymbol{a}^{\top} \boldsymbol{X}^{-1} \boldsymbol{b}}{\partial \boldsymbol{X}}=-\left(\boldsymbol{X}^{-1}\right)^{\top} \boldsymbol{a} b^{\top}\left(\boldsymbol{X}^{-1}\right)^{\top}\\ &\frac{\partial \boldsymbol{x}^{\top} \boldsymbol{a}}{\partial \boldsymbol{x}}=\boldsymbol{a}^{\top}\\ &\frac{\partial \boldsymbol{a}^{\top} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{a}^{\top}\\ &\frac{\partial \boldsymbol{a}^{\top} \boldsymbol{X} \boldsymbol{b}}{\partial \boldsymbol{X}}=\boldsymbol{a} \boldsymbol{b}^{\top}\\ &\frac{\partial \boldsymbol{x}^{\top} \boldsymbol{B} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{x}^{\top}\left(\boldsymbol{B}+\boldsymbol{B}^{\top}\right)\\ &\frac{\partial}{\partial s}(x-A s)^{\top} W(x-A s)=-2(x-A s)^{\top} W A \quad \text { for symmetric } W\\ &(5.108) \end{aligned} ∂X∂f(X)⊤=(∂X∂f(X))⊤∂X∂tr(f(X))=tr(∂X∂f(X))∂X∂det(f(X))=det(f(X))tr(f(X)−1∂X∂f(X))∂X∂f(X)−1=−f(X)−1∂X∂f(X)f(X)−1∂X∂a⊤X−1b=−(X−1)⊤ab⊤(X−1)⊤∂x∂x⊤a=a⊤∂x∂a⊤x=a⊤∂X∂a⊤Xb=ab⊤∂x∂x⊤Bx=x⊤(B+B⊤)∂s∂(x−As)⊤W(x−As)=−2(x−As)⊤WA for symmetric W(5.108)
计算 ∂ x ⊤ B x ∂ x = x ⊤ ( B + B ⊤ ) \frac{\partial x^\top Bx}{\partial x}=x^\top(B+B^\top) ∂x∂x⊤Bx=x⊤(B+B⊤):
反向传播和自动微分(Backpropagation and Automatic Differentiation)
为了计算损失函数(Loss Function)的最小值,这时候需要对损失函数对其所有的参数求偏导,也就是求出损失函数的梯度。但是用传统的链式法则会使得中间步骤十分繁琐,所以有了反向传播算法(Backpropagation Algorithm)可以有效地解决损失函数的梯度的问题,并且运算速度与传统的链式法则的计算方式相同。
深度网络的梯度(Gradients in a Deep Network)
在深度学习中,一个函数通常是由许多的函数复合而成的。
y
=
(
f
K
∘
f
K
−
1
∘
⋯
∘
f
1
)
(
x
)
=
f
K
(
f
K
−
1
(
⋯
(
f
1
(
x
)
)
⋯
)
)
\boldsymbol{y}=\left(f_{K} \circ f_{K-1} \circ \cdots \circ f_{1}\right)(\boldsymbol{x})=f_{K}\left(f_{K-1}\left(\cdots\left(f_{1}(\boldsymbol{x})\right) \cdots\right)\right)
y=(fK∘fK−1∘⋯∘f1)(x)=fK(fK−1(⋯(f1(x))⋯))
后一层神经元会使用前一层神经元的输出值作为该层的输入值,所以有: f i ( x i − 1 ) = σ ( A i − 1 x i − 1 + b i − 1 ) , σ f_i(x_{i-1})=\sigma(\boldsymbol A_{i-1}x_{i-1}+b_{i-1}),\quad \sigma fi(xi−1)=σ(Ai−1xi−1+bi−1),σ 为激活函数. x i − 1 x_{i-1} xi−1是第i层的输出值。

为了训练这个神经网络,我们需要求解出损失函数梯度。
假设:
f
0
:
=
x
f
i
:
=
σ
i
(
A
i
−
1
f
i
−
1
+
b
i
−
1
)
,
i
=
1
,
…
,
K
f_{0}:=x \\ f_{i}:=\sigma_{i}\left(A_{i-1} f_{i-1}+b_{i-1}\right), \quad i=1, \ldots, K
f0:=xfi:=σi(Ai−1fi−1+bi−1),i=1,…,K
损失函数为:
L
(
θ
)
=
∥
y
−
f
K
(
θ
,
x
)
∥
2
,
θ
=
{
A
0
,
b
0
,
…
,
A
K
−
1
,
b
K
−
1
}
L(\theta)=\|y-f_K(\theta,x)\|^2,\quad \theta=\{\boldsymbol A_0,\boldsymbol b_0,\dots, \boldsymbol A_{K-1},\boldsymbol b_{K-1}\}
L(θ)=∥y−fK(θ,x)∥2,θ={A0,b0,…,AK−1,bK−1}
要求解这个函数的最小值,我们需要对损失函数求偏导。
∂
L
∂
θ
K
−
1
=
∂
L
∂
f
K
∂
f
K
∂
θ
K
−
1
∂
L
∂
θ
K
−
2
=
∂
L
∂
f
K
∂
f
K
∂
f
K
−
1
∂
f
K
−
1
∂
θ
K
−
2
∂
L
∂
θ
K
−
3
=
∂
L
∂
f
K
∂
f
K
∂
f
K
−
1
∂
f
K
−
1
∂
f
K
−
2
∂
f
K
−
2
∂
θ
K
−
3
∂
L
∂
θ
i
=
∂
L
∂
f
K
∂
f
K
∂
f
K
−
1
⋯
∂
f
i
+
2
∂
f
i
+
1
∂
f
i
+
1
∂
θ
i
\begin{aligned} \frac{\partial L}{\partial \boldsymbol{\theta}_{K-1}} &=\frac{\partial L}{\partial \boldsymbol{f}_{K}} \frac{\partial \boldsymbol{f}_{K}}{\partial \boldsymbol{\theta}_{K-1}} \\ \frac{\partial L}{\partial \boldsymbol{\theta}_{K-2}} &=\frac{\partial L}{\partial \boldsymbol{f}_{K}}\frac{\partial f_{K}}{\partial f_{K-1}} \frac{\partial \boldsymbol{f}_{K-1}}{\partial \boldsymbol{\theta}_{K-2}}\\ \frac{\partial L}{\partial \boldsymbol{\theta}_{K-3}} &=\frac{\partial L}{\partial \boldsymbol{f}_{K}} \frac{\partial f_{K}}{\partial f_{K-1}} \frac{\partial \boldsymbol{f}_{K-1}}{\partial f_{K-2}} \frac{\partial \boldsymbol{f}_{K-2}}{\partial \boldsymbol{\theta}_{K-3}} \\ \frac{\partial L}{\partial \boldsymbol{\theta}_{i}} &=\frac{\partial L}{\partial \boldsymbol{f}_{K}} \frac{\partial f_{K}}{\partial f_{K-1}} \cdots \frac{\partial f_{i+2}}{\partial f_{i+1}} \frac{\partial \boldsymbol{f}_{i+1}}{\partial \boldsymbol{\theta}_{i}} \end{aligned}
∂θK−1∂L∂θK−2∂L∂θK−3∂L∂θi∂L=∂fK∂L∂θK−1∂fK=∂fK∂L∂fK−1∂fK∂θK−2∂fK−1=∂fK∂L∂fK−1∂fK∂fK−2∂fK−1∂θK−3∂fK−2=∂fK∂L∂fK−1∂fK⋯∂fi+1∂fi+2∂θi∂fi+1
这样看来,当我们需要计算
∂
L
∂
θ
i
\frac{\partial L}{\partial\boldsymbol \theta_i}
∂θi∂L时,我们可以利用之前的
∂
L
∂
θ
i
+
1
\frac{\partial L}{\partial\boldsymbol \theta_{i+1}}
∂θi+1∂L简化计算。
∂
L
∂
θ
i
=
∂
L
∂
θ
i
+
1
∂
f
i
+
1
∂
θ
i
\frac{\partial L}{\partial \boldsymbol\theta_i}=\frac{\partial L}{\partial \boldsymbol\theta_{i+1}}\frac{\partial \boldsymbol f_{i+1}}{\partial \boldsymbol\theta_i}
∂θi∂L=∂θi+1∂L∂θi∂fi+1

自动微分(Automatic Differentiation)
反向传播算法实际上时自动微分中的一个特例。自动微分类似计算的时候用的还原法,将这些中间步骤用一个变量表示出来:
y
=
f
(
g
(
h
(
x
)
)
)
=
f
(
g
(
h
(
w
0
)
)
)
=
f
(
g
(
w
1
)
)
=
f
(
w
2
)
=
w
3
y=f(g(h(x)))=f(g(h(w_0)))=f(g(w_1))=f(w_2)=w_3
y=f(g(h(x)))=f(g(h(w0)))=f(g(w1))=f(w2)=w3
原始的链式法则:
d
y
d
x
=
d
y
d
w
2
d
w
2
d
w
1
d
w
1
d
x
=
d
f
(
w
2
)
d
w
2
d
g
(
w
1
)
d
w
1
d
h
(
w
0
)
d
x
\frac {dy}{dx}=\frac{dy}{dw_2}\frac{dw_2}{dw_1}\frac{dw_1}{dx}=\frac{df(w_2)}{dw_2}\frac{dg(w_1)}{dw_1}\frac{dh(w_0)}{dx}
dxdy=dw2dydw1dw2dxdw1=dw2df(w2)dw1dg(w1)dxdh(w0)
自动微分有两种模式:向前模式(forward mode)和向后模式(reverse mode)
向前模式就是从内层函数到外层函数逐步进行求导,向后模式则是相反。
使用计算图(computational graphs),每个节点代表一个计算过程中的中间变量。
例如:
f
(
x
)
=
x
2
+
exp
(
x
2
)
+
cos
(
x
2
+
exp
(
x
2
)
)
f(x)=\sqrt{x^{2}+\exp \left(x^{2}\right)}+\cos \left(x^{2}+\exp \left(x^{2}\right)\right)
f(x)=x2+exp(x2)+cos(x2+exp(x2))用计算图可以表示为:

可以描述为:
F
o
r
i
=
d
+
1
,
…
,
D
:
x
i
=
g
i
(
x
p
a
(
x
i
)
)
For\ \ i=d+1,\dots, D :\quad x_i=g_i(x_{pa(x_i)})
For i=d+1,…,D:xi=gi(xpa(xi))
其中,
x
P
a
(
x
i
)
x_{Pa(x_i)}
xPa(xi)表示节点
x
i
x_i
xi的父节点。
g
i
(
⋅
)
g_i(\cdot)
gi(⋅)表示节点对应的计算函数。
这部分没什么弄懂,后续继续补充。
计算图的那个部分。
利用上面的关系可以得出:
d f d x i = ∑ j : i ∈ P a ( j ) d f d x i d x j d x i = ∑ j : i ∈ P a ( j ) d f d x j d g i d x i \frac{df}{dx_i}=\sum_{j:i\in Pa(j)}\frac{df}{dx_i}\frac{dx_j}{dx_i}=\sum_{j:i\in Pa(j)}\frac{df}{dx_j}\frac{dg_i}{dx_i} dxidf=j:i∈Pa(j)∑dxidfdxidxj=j:i∈Pa(j)∑dxjdfdxidgi
这实际上就是利用链式法则求解出对中间变量的微分。对最后一个中间变量的微分为1
符号微分(Symbolic differentiation)之所以复杂是因为在运算过程中并没有中间变量,所以想要直接编码解决难度较大
高阶偏导数(Higher-Order Derivatives)
当我们想要用牛顿法进行优化的时候,二阶偏导数就不得不被使用了。
有一个符号需要注意:
∂
2
f
∂
x
∂
y
\frac {\partial^2 f}{\partial x\partial y}
∂x∂y∂2f这个意思时先对y求导,然后再对x求导。
海森矩阵(Hessian Matrix)
海森矩阵存储函数的二阶偏导数。
∇
x
,
y
2
f
(
x
,
y
)
=
H
=
[
∂
2
f
∂
x
2
∂
2
f
∂
x
∂
y
∂
2
f
∂
x
∂
y
∂
2
f
∂
y
2
]
\nabla^2_{x,y}f(x,y)=\boldsymbol{H}=\left[\begin{array}{cc}\frac{\partial^{2} f}{\partial x^{2}} & \frac{\partial^{2} f}{\partial x \partial y} \\ \frac{\partial^{2} f}{\partial x \partial y} & \frac{\partial^{2} f}{\partial y^{2}}\end{array}\right]
∇x,y2f(x,y)=H=[∂x2∂2f∂x∂y∂2f∂x∂y∂2f∂y2∂2f]
表示函数在
(
x
,
y
)
(x,y)
(x,y)处的曲率
线性化和多元泰勒级数(Linearization and Multivariate Taylor Series)
假设一个函数:
f
:
R
D
→
R
x
↦
f
(
x
)
,
x
∈
R
D
\begin{aligned} f: \mathbb{R}^{D} & \rightarrow \mathbb{R} \\ \quad \boldsymbol{x} & \mapsto f(\boldsymbol{x}), \quad \boldsymbol{x} \in \mathbb{R}^{D} \end{aligned}
f:RDx→R↦f(x),x∈RD
在
x
0
x_0
x0处光滑,设
δ
:
=
x
−
x
0
\delta := x-x_0
δ:=x−x0,所以:
f
(
x
)
=
∑
k
=
0
∞
D
x
k
f
(
x
0
)
k
!
δ
k
f(x)=\sum^\infty_{k=0}\frac{D^k_\boldsymbol xf(x_0)}{k!}\delta^k
f(x)=k=0∑∞k!Dxkf(x0)δk
为
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处的多元泰勒公式。其中,
D
x
k
f
(
x
0
)
D^k_\boldsymbol xf(x_0)
Dxkf(x0),表示
f
(
x
)
f(x)
f(x)对x的k阶偏导。
D
x
k
f
(
x
0
)
D^k_\boldsymbol xf(x_0)
Dxkf(x0)和
δ
k
\delta^k
δk都是k阶张量,其中:
δ
k
∈
R
D
×
D
×
…
×
D
⏞
k
times
\boldsymbol{\delta}^{k} \in \mathbb{R} \overbrace{D \times D \times \ldots \times D}^{k \text { times }}
δk∈RD×D×…×D
k times
δ
3
:
=
δ
⊗
δ
⊗
δ
,
δ
3
[
i
,
j
,
k
]
=
δ
[
i
]
δ
[
j
]
δ
[
k
]
\boldsymbol{\delta}^{3}:=\boldsymbol{\delta} \otimes \boldsymbol{\delta} \otimes \boldsymbol{\delta}, \quad \boldsymbol{\delta}^{3}[i, j, k]=\delta[i] \delta[j] \delta[k]
δ3:=δ⊗δ⊗δ,δ3[i,j,k]=δ[i]δ[j]δ[k]
所以,(第一个中括号是前面偏导向量的索引)
D
x
k
f
(
x
0
)
δ
k
=
∑
i
1
=
1
D
⋯
∑
i
k
=
1
D
D
x
k
f
(
x
0
)
[
i
1
,
…
,
i
k
]
δ
[
i
1
]
⋯
δ
[
i
k
]
D_{\boldsymbol{x}}^{k} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{k}=\sum_{i_{1}=1}^{D} \cdots \sum_{i_{k}=1}^{D} D_{\boldsymbol{x}}^{k} f\left(\boldsymbol{x}_{0}\right)\left[i_{1}, \ldots, i_{k}\right] \delta\left[i_{1}\right] \cdots \delta\left[i_{k}\right]
Dxkf(x0)δk=i1=1∑D⋯ik=1∑DDxkf(x0)[i1,…,ik]δ[i1]⋯δ[ik]
下面是上式的前三项:
k
=
0
,
…
,
3
and
δ
:
=
x
−
x
0
:
k
=
0
:
D
x
0
f
(
x
0
)
δ
0
=
f
(
x
0
)
∈
R
k
=
1
:
D
x
1
f
(
x
0
)
δ
1
=
∇
x
f
(
x
0
)
⏟
1
×
D
δ
⏟
D
×
1
=
∑
i
=
1
D
∇
x
f
(
x
0
)
[
i
]
δ
[
i
]
∈
R
k
=
2
:
D
x
2
f
(
x
0
)
δ
2
=
tr
(
H
(
x
0
)
⏟
D
×
D
δ
⏟
D
×
1
δ
⊤
⏟
1
×
D
)
=
δ
⊤
H
(
x
0
)
δ
=
∑
i
=
1
D
∑
j
=
1
D
H
[
i
,
j
]
δ
[
i
]
δ
[
j
]
∈
R
k
=
3
:
D
x
3
f
(
x
0
)
δ
3
=
∑
i
=
1
D
∑
j
=
1
D
∑
k
=
1
D
D
x
3
f
(
x
0
)
[
i
,
j
,
k
]
δ
[
i
]
δ
[
j
]
δ
[
k
]
∈
R
\begin{array}{l} k=0, \ldots, 3 \text { and } \delta:=x-x_{0}: \\ k=0: D_{\boldsymbol{x}}^{0} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{0}=f\left(\boldsymbol{x}_{0}\right) \in \mathbb{R} \\ k=1: D_{\boldsymbol{x}}^{1} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{1}=\underbrace{\nabla_{\boldsymbol{x}} f\left(\boldsymbol{x}_{0}\right)}_{1 \times D} \underbrace{\delta}_{D \times 1}=\sum_{i=1}^{D} \nabla_{\boldsymbol{x}} f\left(\boldsymbol{x}_{0}\right)[i] \delta[i] \in \mathbb{R} \\ k=2: D_{\boldsymbol{x}}^{2} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{2}=\operatorname{tr}(\underbrace{\boldsymbol{H}\left(\boldsymbol{x}_{0}\right)}_{D \times D} \underbrace{\delta}_{D \times 1} \underbrace{\delta^{\top}}_{1 \times D})=\delta^{\top} \boldsymbol{H}\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta} \\ =\sum_{i=1}^{D} \sum_{j=1}^{D} H[i, j] \delta[i] \delta[j] \in \mathbb{R} \\ k=3: D_{\boldsymbol{x}}^{3} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{3}=\sum_{i=1}^{D} \sum_{j=1}^{D} \sum_{k=1}^{D} D_{x}^{3} f\left(\boldsymbol{x}_{0}\right)[i, j, k] \delta[i] \delta[j] \delta[k] \in \mathbb{R} \end{array}
k=0,…,3 and δ:=x−x0:k=0:Dx0f(x0)δ0=f(x0)∈Rk=1:Dx1f(x0)δ1=1×D
∇xf(x0)D×1
δ=∑i=1D∇xf(x0)[i]δ[i]∈Rk=2:Dx2f(x0)δ2=tr(D×D
H(x0)D×1
δ1×D
δ⊤)=δ⊤H(x0)δ=∑i=1D∑j=1DH[i,j]δ[i]δ[j]∈Rk=3:Dx3f(x0)δ3=∑i=1D∑j=1D∑k=1DDx3f(x0)[i,j,k]δ[i]δ[j]δ[k]∈R
其中
H
(
x
0
)
\boldsymbol H(x_0)
H(x0)表示在
x
0
x_0
x0处的海森矩阵。
证明?
k = 2 : D x 2 f ( x 0 ) δ 2 = tr ( H ( x 0 ) ⏟ D × D δ ⏟ D × 1 δ ⊤ ⏟ 1 × D ) = δ ⊤ H ( x 0 ) δ = ∑ i = 1 D ∑ j = 1 D H [ i , j ] δ [ i ] δ [ j ] ∈ R k=2: D_{\boldsymbol{x}}^{2} f\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta}^{2}=\operatorname{tr}(\underbrace{\boldsymbol{H}\left(\boldsymbol{x}_{0}\right)}_{D \times D} \underbrace{\delta}_{D \times 1} \underbrace{\delta^{\top}}_{1 \times D})=\delta^{\top} \boldsymbol{H}\left(\boldsymbol{x}_{0}\right) \boldsymbol{\delta} \\ =\sum_{i=1}^{D} \sum_{j=1}^{D} H[i, j] \delta[i] \delta[j] \in \mathbb{R} k=2:Dx2f(x0)δ2=tr(D×D H(x0)D×1 δ1×D δ⊤)=δ⊤H(x0)δ=i=1∑Dj=1∑DH[i,j]δ[i]δ[j]∈R
补充
反向传播(推导)
我们想要求的是对损失函数对参数的求导的结果:
d
L
d
v
i
,
i
≥
N
−
M
+
1
\frac{dL}{dv_i},i\ge N-M+1
dvidL,i≥N−M+1
利用链式法则:
d
L
d
v
i
=
∑
j
:
i
∈
P
a
(
j
)
d
L
d
v
i
d
v
i
d
v
j
\frac{dL}{dv_i}=\sum_{j:i\in Pa(j)}\frac{dL}{dv_i}\frac{dv_i}{dv_j}
dvidL=j:i∈Pa(j)∑dvidLdvjdvi
回想我们计算激活值的方法:
v
i
=
σ
i
(
w
i
⋅
v
P
a
(
i
)
)
v_i=\sigma_i(w_i\cdot v_{Pa(i)})
vi=σi(wi⋅vPa(i))
所以我们可以计算:
d
v
i
d
v
j
=
σ
i
′
(
w
i
⋅
v
P
a
(
i
)
)
w
i
q
,
P
a
(
i
)
q
=
j
\frac{dv_i}{dv_j}=\sigma_i'(\boldsymbol w_i\cdot \boldsymbol v_{Pa(i)})w_{iq},Pa(i)_q=j
dvjdvi=σi′(wi⋅vPa(i))wiq,Pa(i)q=j
举个例子,假设
P
a
(
i
)
=
(
2
,
7
,
9
)
Pa(i)=(2,7,9)
Pa(i)=(2,7,9),则激活值为:
v
i
=
σ
i
(
w
i
⋅
v
(
2
,
7
,
9
)
)
v_i=\sigma_i(\boldsymbol w_i\cdot \boldsymbol v_{(2,7,9)})
vi=σi(wi⋅v(2,7,9))
展开即为下面这些式子:
d
v
i
d
v
2
=
σ
i
′
(
w
i
⋅
v
(
2
,
7
,
9
)
)
w
i
1
d
v
i
d
v
7
=
σ
i
′
(
w
i
⋅
v
(
2
,
7
,
9
)
)
w
i
2
d
v
i
d
v
9
=
σ
i
′
(
w
i
⋅
v
(
2
,
7
,
9
)
)
w
i
3
.
\begin{aligned} \frac{d v_{i}}{d v_{2}} &=\sigma_{i}^{\prime}\left(\mathbf{w}_{i} \cdot \mathbf{v}_{(2,7,9)}\right) w_{i 1} \\ \frac{d v_{i}}{d v_{7}} &=\sigma_{i}^{\prime}\left(\mathbf{w}_{i} \cdot \mathbf{v}_{(2,7,9)}\right) w_{i 2} \\ \frac{d v_{i}}{d v_{9}} &=\sigma_{i}^{\prime}\left(\mathbf{w}_{i} \cdot \mathbf{v}_{(2,7,9)}\right) w_{i 3} . \end{aligned}
dv2dvidv7dvidv9dvi=σi′(wi⋅v(2,7,9))wi1=σi′(wi⋅v(2,7,9))wi2=σi′(wi⋅v(2,7,9))wi3.
我们用
v
i
′
=
σ
i
′
(
w
i
⋅
v
P
a
(
i
)
)
v_i'=\sigma'_i(\boldsymbol w_i\cdot \boldsymbol v_{Pa(i)})
vi′=σi′(wi⋅vPa(i))带入到原先的式子中:
d
v
i
d
v
j
=
v
i
′
w
i
q
,
P
a
(
i
)
q
=
j
\frac{dv_i}{dv_j}=v_i'w_{iq},Pa(i)_q=j
dvjdvi=vi′wiq,Pa(i)q=j
对应的向量形式为:
d
v
i
d
v
P
a
(
i
)
=
v
i
′
w
i
\frac{dv_i}{d\mathbf v_{Pa(i)}}= v'_i\mathbf w_i
dvPa(i)dvi=vi′wi
于是我们可以很容易得到:(带入已知式)
d
L
d
w
i
=
d
L
d
v
i
d
v
i
d
w
i
=
d
L
d
v
i
σ
i
′
(
w
⋅
v
P
a
(
i
)
)
v
P
a
(
i
)
=
d
L
d
v
i
v
i
′
v
P
a
(
i
)
\begin{aligned} \frac{d L}{d \mathbf{w}_{i}} &=\frac{d L}{d v_{i}} \frac{d v_{i}}{d \mathbf{w}_{i}} \\ &=\frac{d L}{d v_{i}} \sigma_{i}^{\prime}\left(\mathbf{w} \cdot \mathbf{v}_{\mathrm{Pa}(i)}\right) \mathbf{v}_{\mathrm{Pa}(i)} \\ &=\frac{d L}{d v_{i}} v_{i}^{\prime} \mathbf{v}_{\mathrm{Pa}(i)} \end{aligned}
dwidL=dvidLdwidvi=dvidLσi′(w⋅vPa(i))vPa(i)=dvidLvi′vPa(i)









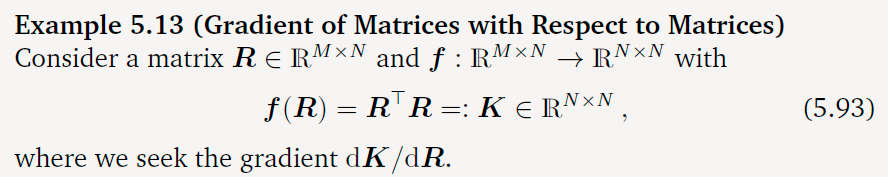













 2237
2237











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








