机器学习中的数学：（三）矩阵分解(Matrix Decompositions)

矩阵分解可以用于压缩矩阵，以尽可能少的空间存储一个矩阵，同时损失尽可能少的信息。同时对数据进行降维还可以减少发生 维度灾难的发生。

维数灾难： 当数据维度提升的时候，因为空间体积提升过快，因而可用数据变得很稀疏。然而在高维空间中，所有的数据都很稀疏，从很多角度看都不相似，因而平常使用的数据组织策略变得极其低效。


在机器学习问题中，需要在高维特征空间（每个特征都能够取一系列可能值）的有限数据样本中学习一种“自然状态”（可能是无穷分布），要求有相当数量的训练数据含有一些样本组合。给定固定数量的训练样本，其预测能力随着维度的增加而减小，这就是所谓的Hughes影响或Hughes现象（以Gordon F. Hughes命名）。
------Wiki
个人理解：随着维度的升高数据之间的距离加大，这导致数据组合而成的用于最终判断的特征难以被发现

行列式与迹（Determinant and Trace）

行列式（Dterminant）

行列式可以看成将一个方阵映射成一个实数。（只有方阵才有行列式）
可以将行列式用于判断一个方阵是否可逆：

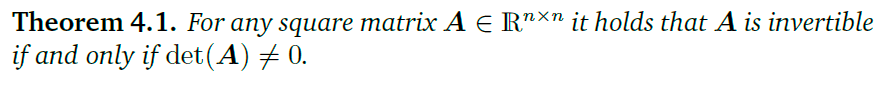
对于上/下三角矩阵的行列式的值为:
$$\det (\mathbf{T})=\prod _{i=1}^n{T}_{ii}$$

对于n阶行列的计算，可以使用拉普拉斯展开(Laplace Expansion)

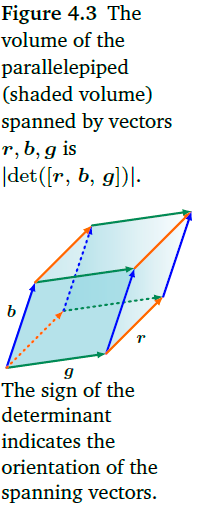
行列式的几何含义就是带有符号的多边形的体积，这个多边形是由行列式所对应的列向量通过平移之后组成的.注意到当至少其中的两个向量重合的时候，也就是这两个向量线性相关的时候，他们组成的几何体的体积为0，所以这时候他们组成的方阵的行列式为0.

行列式的一些性质：

迹(Trace)

假设$f(x)={\prod }_{i=1}^k(x-{\lambda }_i{)}^{d_i}$是矩阵A的特征多项式，那么A的迹为：
$$\mathrm{tr}(\mathbf{A})=\sum _{i=1}^k{d}_i{\lambda }_i$$

对于一个方阵的迹就是它所有对角线元素的和：

$$tr(\mathbf{A}):=\sum _{i=1}^n{a}_{ii}$$
迹的一些性质：


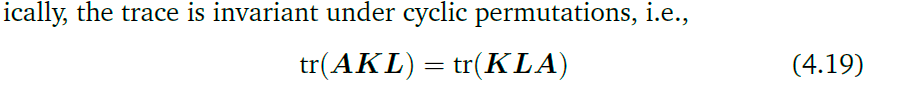
假设$\mathbf{B}、\mathbf{A}$是向量空间U的两个基向量，所以一定存在一个向量$\mathbf{S}$,使得$\mathbf{B}={\mathbf{S}}^{-1}\mathbf{A}\mathbf{S}$:
$$\mathrm{tr}(\mathbf{B})=\mathrm{tr}\left({\mathbf{S}}^{-1}\mathbf{A}\mathbf{S}\right)\stackrel{(4.19)}{=}\mathrm{tr}\left(\mathbf{A}\mathbf{S}{\mathbf{S}}^{-1}\right)=\mathrm{tr}(\mathbf{A})$$

特征多项式：

其中：
$$\begin{gathered} c_0=det(\mathbf{A}) \\ {c}_{n-1}=(-1{)}^{n-1}tr(\mathbf{A}) \end{gathered}$$
特征多项式可以用于求解特征值和特征向量。

特征值与特征向量

特征向量不是唯一的，与特征向量共线的所有向量都是这个矩阵的特征向量。
共线与共向：

特征值是矩阵特征多项式的一个根。
代数重度（algebraic multiplicity）：该特征是特征向量的几重根。
特征空间：特征值对应的特征向量组成的向量空间就是特征空间

有疑问

特征向量所张成的空间就是特征向量通过线性映射之后得到的。而特征向量所对应的特征值的正负对应着特征向量的指向的方向

特征值的几个非常有用的性质：
1.矩阵和他的转置的特征值一样，但是特征向量不一定一样
2.观察特征方程$(\mathbf{A}-\lambda \mathbf{I})\mathbf{x}=0$,这说明$(\mathbf{A}-\lambda \mathbf{I})$对应着核空间

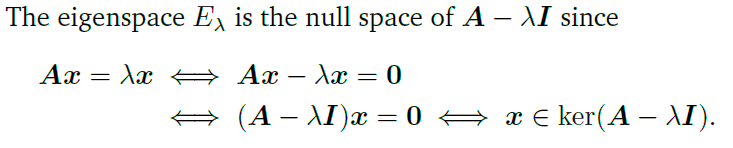
3.相似矩阵（$\tilde{A}=S^{-1}AS$）的特征值保持一致，说明特征值是与基向量无关的（拥有这种性质的还有迹和行列式）
4.正定矩阵拥有正的实特征值。

几何重度（Geometric Multiplicity，特征空间的维度）：
$\lambda$对应的线性无关的特征向量的个数。

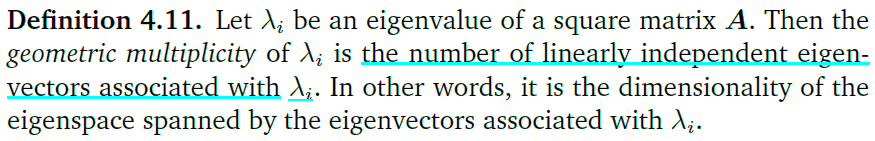
为什么？

二维空间中的几何直观理解：
对于特征方程（$\mathbf{A}\mathbf{x}=\lambda \mathbf{x}$），等式右边是对向量x的一个变换（变换矩阵为A），右边为对x的一个伸展，二者相等，说明在经历过变换之后，x向量只是简单地发生了范数地增长，并没有离开原先地向量空间。而这个变换之后不离开原先向量空间的向量称为特征向量。特征向量组成的向量空间，称为特征空间，在特征空间中的所有向量经过变换之后也不会离开原先的张成空间。向量延展的倍数为变换矩阵的特征值

特征向量与特征值的求解过程：
由特征方程得到：$(\mathbf{A}-\lambda I)\mathbf{v}=0$当$\vec{\mathbf{v}}$为零向量的时候，等式成立，但是我们想要一个非零向量，所以原来的式子的含义就变成，将一个向量压缩成一个零向量，这就是说在经过变换之后原先的向量发生了降维，这就是说$\mathbf{A}-\lambda I$不是满秩的，就好像是一个三维体经过变换之后变成了二维，这时候变换之后的几何体的体积变成了0，也就是相对应的行列式变成了0，所以$|\mathbf{A}-\lambda I|=0、det(\mathbf{A}-\lambda I)=0$

下图是不同类型的线性映射时候特征值和行列式的情况：
其中
$$\begin{gathered} {\mathbf{A}}_1=\left[\begin{array}{c}\frac{1}{2}0\\ 02\end{array}\right] \\ {\mathbf{A}}_2=\left[\begin{array}{c}1\frac{1}{2}\\ 01\end{array}\right] \\ {\mathbf{A}}_3=\left[\begin{array}{c}\cos (\frac{\pi }{6})-\sin (\frac{\pi }{6})\\ \sin (\frac{\pi }{6})\cos (\frac{\pi }{6})\end{array}\right]=\frac{1}{2}\left[\begin{array}{c}\sqrt{3}-1\\ 1\sqrt{3}\end{array}\right] \\ {\mathbf{A}}_4=\left[\begin{array}{c}1-1\\ -11\end{array}\right] \end{gathered}$$

为什么最后一个的行列式的值发生了变化？

每一个特征空间在变换中对应着唯一一个特征值（倍数），所以当倍数（特征值）全部都是不同的时候，说明有所有的特征向量都是线性无关的。

亏损矩阵

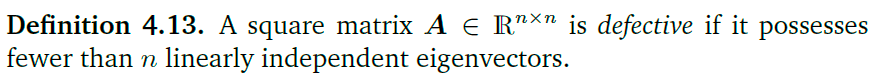
对于一个非亏损矩阵（$\in {\mathbb{R}}^{n\times n}$）不一定需要n个不同的特征值，但是一定需要n个特征向量组成${\mathbb{R}}^{n\times n}$的基。（注意到不同的向量在变换的时候延伸的倍数是可以一样的，所以会有一个特征值对应几个特征向量的情况）

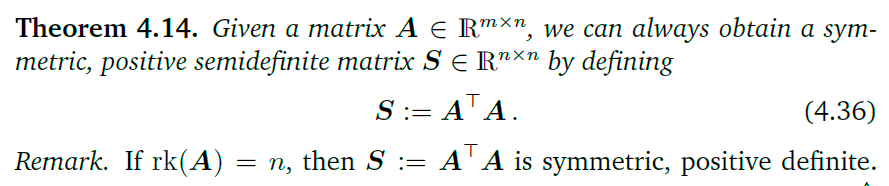
谱定律：

这说明一个对称矩阵可以进行特征分解,也就是说能够找到特征向量对应的规范正交基，使得$\mathbf{A}=\mathbf{P}\mathbf{D}{\mathbf{P}}^{-1}$其中D为对角矩阵，P由特征向量组成。

行列式与迹的意义：分别与面积（体积）和周长相关

柯列斯基分解（Cholesky Decomposition）

计算方式：

这在深度学习中有很多的应用，同时还可以用于计算行列式（上下三角矩阵的行列式非常好计算）

特征分解和对角化

可对角化的条件：


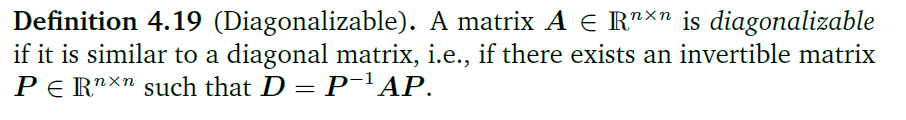
这需要P矩阵是满秩的
特征分解

这实际上就是A与D相似。P由A的特征向量组成，D由A的特征值组成（对角矩阵）

如何理解相似矩阵？
如何理解谱定理？

矩阵分解的几何直观理解

各部分对应的变换还是不是很清楚。
特征值分解可以这样理解，首先先进行一次基变换，将正交基变换至由特征向量组成的向量空间中，然后进行延展（这就是变换矩阵A对应在特征向量中的变换Ax=$\lambda x$）,最后将向量空间复原到原先的向量空间中。

对待方程$\mathbf{A}={\mathbf{P}}^{-1}\mathbf{D}\mathbf{P}$,可以这样想，单位矩阵经过A矩阵变换之后等价于${\mathbf{P}}^{-1}\mathbf{D}\mathbf{P}$三个矩阵变化之后的结果。
将一个矩阵分解之后，可以很方便地计算矩阵地行列式和n次方。
$$det(\mathbf{A})=det(\mathbf{P}\mathbf{D}{\mathbf{P}}^{-1})=det(\mathbf{P})\ast det(\mathbf{D})\ast det({\mathbf{P}}^{-1})=\prod _i{d}_{ii}$$

奇异值分解（Singular Value Decomposition，SVD）

相对于特征值分解，奇异值分解使用范围更广，它不要求分解的矩阵是方阵。

$u_i$称为左奇异向量；$v_j$称为右奇异向量。

$\Sigma$矩阵起到拓展维度的作用，所以：

SVD的几何直观解释

奇异值分解其实和特征值分解类似，只是在延伸的时候加了一些东西，这是因为矩阵为非方阵的时候，这样的变换会使向量发生维度的变化，所以$\Sigma$矩阵在不是方阵的情况下，不仅仅使向量进行相对应的变换，还将维度进行了提升。

$V^T$起到旋转的作用，$\Sigma$起到拓展上域（codomain，到达域）维度的作用，最后U帮助向量升维。

上域

一个变换实例：

求解矩阵的SVD

对于一个对称正定矩阵（SPD矩阵）有:$S=S^T=PD{P}^T$

所以一个SDP矩阵的SVD就是它的特征值分解。

计算一个矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times n}$,等价于求解上域（codomain）${\mathbb{R}}^m$和定义域（domain）${\mathbb{R}}^n$的规范正交基

What’s the graphic intuitions?And why?

求解右奇异向量

由谱定理得知，对称矩阵的特征向量组成规范正交基，也就是说对称矩阵能够相似对角化。而我们可以通过$A{A}^T$的方式得到一个半正定的对称矩阵。

$${\mathbf{A}}^{\top }\mathbf{A}=\mathbf{P}\mathbf{D}{\mathbf{P}}^{\top }=\mathbf{P}\left[\begin{array}{ccc}{\lambda }_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\lambda }_n\end{array}\right]{\mathbf{P}}^{\top }$$
将SVD带入：
$${\mathbf{A}}^{\top }\mathbf{A}={\left(\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\right)}^{\top }\left(\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\right)=\mathbf{V}{\mathbf{\Sigma }}^{\top }{\mathbf{U}}^{\top }\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }$$
由于$\mathbf{U}$是正交矩阵，所以$\mathbf{U}{\mathbf{U}}^{\top }=\mathbf{I}$:
$${\mathbf{A}}^{\top }\mathbf{A}=\mathbf{V}{\mathbf{\Sigma }}^{\top }\mathbf{\Sigma }{\mathbf{V}}^{\top }=\mathbf{V}\left[\begin{array}{ccc}{\sigma }_1^2& 0& 0\\ 0& \ddots & 0\\ 0& 0& {\sigma }_n^2\end{array}\right]{\mathbf{V}}^{\top }$$
由此可以得出，A的SVD的奇异值就是$A{A}^{\top }$的特征值的开根号的结果。其特征矩阵就是右奇异矩阵。

对于左奇异矩阵采取相似的方式：
$$\begin{array}{rl}\mathbf{A}{\mathbf{A}}^{\top }& =\left(\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\right){\left(\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\right)}^{\top }=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }\mathbf{V}{\mathbf{\Sigma }}^{\top }{\mathbf{U}}^{\top }\\ & =\mathbf{U}\left[\begin{array}{ccc}{\sigma }_1^2& 0& 0\\ 0& \ddots & 0\\ 0& 0& {\sigma }_m^2\end{array}\right]{\mathbf{U}}^{\top }.\end{array}$$
现在将左右奇异矩阵联系起来：
由于$\mathbf{U}$中的向量$v_i$在经过A矩阵变换之后仍旧是正交向量，因为，$${\left(\mathbf{A}{\mathbf{v}}_i\right)}^{\top }\left(\mathbf{A}{\mathbf{v}}_j\right)={\mathbf{v}}_i^{\top }\left({\mathbf{A}}^{\top }\mathbf{A}\right){\mathbf{v}}_j={\mathbf{v}}_i^{\top }\left({\lambda }_j{\mathbf{v}}_j\right)={\lambda }_j{\mathbf{v}}_i^{\top }{\mathbf{v}}_j=0，i\ne j$$
单位化右奇异向量的像域：
$${\mathbf{u}}_i:=\frac{\mathbf{A}{\mathbf{v}}_i}{\Vert \mathbf{A}{\mathbf{v}}_i\Vert }=\frac{1}{\sqrt{{\lambda }_i}}\mathbf{A}{\mathbf{v}}_i=\frac{1}{{\sigma }_i}\mathbf{A}{\mathbf{v}}_i$$

二者的关系？

由上得到奇异方程：

$$\mathbf{A}{\mathbf{v}}_i={\sigma }_i{\mathbf{u}}_i,i=1,\dots ,r$$
于是有：
$$\mathbf{A}\mathbf{V}=\Sigma \mathbf{U}$$
移项得：
$$\mathbf{A}=\mathbf{U}\Sigma {\mathbf{V}}^{\top }$$
这就是矩阵A的SVD。

矩阵逼近（Matrix Approximation）

外积：

与内积不同，当两个向量相乘的时候，外积得到的是一个矩阵。有之前的SVD分解式，可以得到下式：
$$\mathbf{A}=\sum _{i=1}^r{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^{\top }=\sum _{i=1}^r{\sigma }_i{\mathbf{A}}_i$$

但是加入我们不讲所有的外积都加上的话，得到一个秩为$k(k<r)$的矩阵，这个称为k秩逼近（rank-k approximation）

$$\hat{\mathbf{A}}(k):=\sum _{i=1}^k{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^{\top }=\sum _{i=1}^k{\sigma }_i{\mathbf{A}}_i$$

谱模（spectral norm）

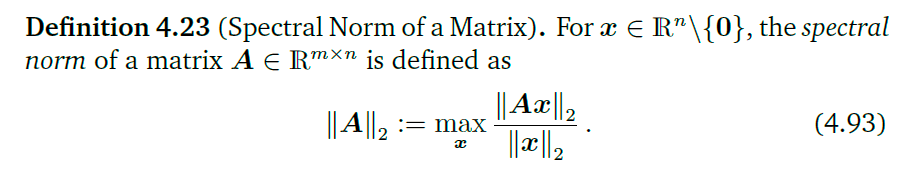
谱模表示，一个向量在经历矩阵A的变换之后最长可以变成多长（下标2代表的是欧几里得空间）。可以证明，矩阵A的谱模就是它的最大的奇异值

埃卡特-杨定理

这个定理量化了矩阵近似会造成的误差。

证明过程？

总结