回归的目的就是找到一个函数 f f f,将输入的数据 x ∈ R n \boldsymbol x\in \mathbb R^n x∈Rn映射成 f ( x ) ∈ R f(\boldsymbol x)\in \mathbb R f(x)∈R.数据的观测噪音为: y n = f ( x n ) + ϵ y_n=f(x_n)+\epsilon yn=f(xn)+ϵ,其中 ϵ \epsilon ϵ是一个独立均匀分布的随机变量,描述数据噪音。
噪音理解成预测值与观测值的偏差,准不准确?

问题描述(Problem Formulation)
因为观测噪音的缘故,我们使用概率模型,并且用一个似然函数对噪音进行建模。具体来说,我们考虑以下回归问题的的似然函数:
p
(
y
∣
x
)
=
N
(
y
∣
f
(
x
)
,
σ
2
)
p(y|\boldsymbol x)=\mathcal N(y|f(\boldsymbol x),\sigma^2)
p(y∣x)=N(y∣f(x),σ2)
其中,
x
∈
R
n
\boldsymbol x\in \mathbb R^n
x∈Rn是输入值,
y
∈
R
y\in \mathbb R
y∈R为噪音函数值(目标)
x
\boldsymbol x
x与
y
y
y之间的关系为:
y
=
f
(
x
)
+
ϵ
y= f(\boldsymbol x)+\epsilon
y=f(x)+ϵ
其中,
ϵ
∼
N
(
0
,
σ
2
)
\epsilon \sim\mathcal N(0,\sigma^2)
ϵ∼N(0,σ2)是一个独立均匀的高斯分布。
Our objective is to find a function that is close (similar) to the unknown function f f f that generated the data and that generalizes well.
假设在线性模型的条件下:
p
(
y
∣
x
,
θ
)
=
N
(
y
∣
x
⊤
θ
,
σ
2
)
⇔
y
=
x
⊤
θ
+
ϵ
,
ϵ
∼
N
(
0
,
σ
2
)
p(y|\boldsymbol x,\boldsymbol \theta)=\mathcal N(y|\boldsymbol x^\top\boldsymbol\theta,\sigma^2)\Leftrightarrow y=\boldsymbol x^\top\boldsymbol\theta+\epsilon,\quad \epsilon \sim \mathcal N(0,\sigma^2)
p(y∣x,θ)=N(y∣x⊤θ,σ2)⇔y=x⊤θ+ϵ,ϵ∼N(0,σ2)
Why?
这里说明一下线性模型的意思,线性代表的是输入数据的线性组合,所以对于 y = ϕ ⊤ ( x ) θ y=\phi^\top(\boldsymbol x)\boldsymbol\theta y=ϕ⊤(x)θ,即使 ϕ ⊤ ( x ) \phi^\top(\boldsymbol x) ϕ⊤(x)是非线性函数,这个模型也是线性模型。
参数估计(Parameter Estimation)
给定一个训练集
D
:
=
{
(
x
1
,
y
1
)
,
⋯
,
(
x
N
,
y
N
)
\mathcal D :=\{(x_1,y_1),\cdots,(x_N,y_N)
D:={(x1,y1),⋯,(xN,yN),包含
N
N
N个输入
x
n
∈
R
D
x_n\in \mathbb R^D
xn∈RD和观测值
y
n
∈
R
,
n
=
1
,
⋯
,
N
y_n\in \mathbb R,n=1,\cdots, N
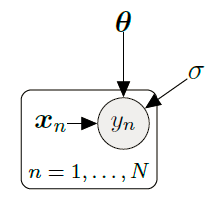
yn∈R,n=1,⋯,N.
用概率图模型(Probabilistic graphical model)可以表示为:
又因为每一个样本又是相互独立的,所以可以将似然方程进行分解:
p
(
Y
∣
X
,
θ
)
=
p
(
y
1
,
⋯
,
y
N
∣
x
1
,
⋯
,
x
N
,
θ
)
=
∏
n
=
1
N
p
(
y
n
∣
x
n
,
θ
)
=
∏
n
=
1
N
N
(
y
n
∣
x
n
⊤
θ
,
σ
2
)
p(\mathcal Y|\mathcal X,\boldsymbol\theta)=p(y_1,\cdots,y_N|\boldsymbol x_1,\cdots,\boldsymbol x_N,\boldsymbol\theta)=\prod^N_{n=1}p(y_n|\boldsymbol x_n,\boldsymbol\theta) = \prod^N_{n=1}\mathcal N(y_n|\boldsymbol x_n^\top\boldsymbol\theta,\sigma^2)
p(Y∣X,θ)=p(y1,⋯,yN∣x1,⋯,xN,θ)=n=1∏Np(yn∣xn,θ)=n=1∏NN(yn∣xn⊤θ,σ2)
接下来详细介绍获取最优化参数的方法。
极大似然估计(Maximum Likelihood Estimation)
我们可以通过极大似然估计得到参数:
θ
M
L
=
arg
max
θ
p
(
Y
∣
X
,
θ
)
\boldsymbol \theta_{ML}=\arg \max_\theta p(\mathcal Y|\mathcal X,\boldsymbol\theta)
θML=argθmaxp(Y∣X,θ)
上面的似然概率不是参数
θ
\theta
θ的分布,而是函数。极大似然估计的目的就是最大化训练数据的概率分布。
在实际过程中,我们常常采用似然对数转换(Log-Transformation)的方式,将问题转化成最小化负对数似然:
−
log
p
(
Y
∣
X
,
θ
)
=
−
log
∏
n
=
1
N
p
(
y
n
∣
x
n
,
θ
)
=
−
∑
n
=
1
N
log
p
(
y
n
∣
x
n
,
θ
)
-\log p(\mathcal Y|\mathcal X,\boldsymbol\theta)=-\log \prod_{n=1}^N p(y_n|\boldsymbol x_n,\boldsymbol\theta)=-\sum^N_{n=1}\log p(y_n|\boldsymbol x_n,\boldsymbol\theta)
−logp(Y∣X,θ)=−logn=1∏Np(yn∣xn,θ)=−n=1∑Nlogp(yn∣xn,θ)
这样做可以将原先的乘积转换成和,
What does this suppose means?
More specifically, numerical underflow will be a problem when we multiply N probabilities, where N is the number of data points, since we cannot represent very small numbers, such as 1 0 256 10^{256} 10256.
由于在线性规划中,似然概率分布满足高斯分布(噪音项 ϵ \epsilon ϵ满足高斯分布),所以可以得到:
??需要补充
Note that:
p ( y ∣ x , θ ) = N ( y ∣ x ⊤ θ , σ 2 ) = 1 2 π σ 2 e − ( y − x ⊤ ) 2 2 σ 2 p(y|x,\theta)=\mathcal N(y|x^\top\theta,\sigma^2)=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(y-x^\top)^2}{2\sigma^2}} p(y∣x,θ)=N(y∣x⊤θ,σ2)=2πσ21e−2σ2(y−x⊤)2
log
p
(
y
n
∣
x
n
,
θ
)
=
−
1
2
σ
2
(
y
n
−
x
n
⊤
θ
)
2
+
const
\log p(y_n|\boldsymbol x_n,\boldsymbol\theta)=-\frac{1}{2\sigma^2}(y_n-\boldsymbol x_n^\top\boldsymbol\theta)^2+\operatorname {const}
logp(yn∣xn,θ)=−2σ21(yn−xn⊤θ)2+const
于是得到损失函数:
L
(
θ
)
:
=
1
2
σ
2
∑
n
=
1
N
(
y
n
−
x
n
⊤
θ
)
2
=
1
2
σ
2
(
y
−
X
θ
)
⊤
(
y
−
X
θ
)
=
1
2
σ
2
∥
y
−
X
θ
∥
2
\begin{aligned} \mathcal{L}(\boldsymbol{\theta}) &:=\frac{1}{2 \sigma^{2}} \sum_{n=1}^{N}\left(y_{n}-\boldsymbol{x}_{n}^{\top} \boldsymbol{\theta}\right)^{2} \\ &=\frac{1}{2 \sigma^{2}}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\theta})^{\top}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\theta})=\frac{1}{2 \sigma^{2}}\|\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\theta}\|^{2} \end{aligned}
L(θ):=2σ21n=1∑N(yn−xn⊤θ)2=2σ21(y−Xθ)⊤(y−Xθ)=2σ21∥y−Xθ∥2
我们将
X
:
=
[
x
1
,
x
2
,
⋯
,
x
N
]
⊤
∈
R
N
×
D
\boldsymbol X:=[x_1,x_2,\cdots,x_N]^\top\in \mathbb R^{N\times D}
X:=[x1,x2,⋯,xN]⊤∈RN×D定义为设计矩阵(Design Matrix)
可以通过求导求解损失函数的最小值:
d
L
d
θ
=
d
d
θ
(
1
2
σ
2
(
y
−
X
θ
)
⊤
(
y
−
X
θ
)
)
=
1
2
σ
2
d
d
θ
(
y
⊤
y
−
2
y
⊤
X
θ
+
θ
⊤
X
⊤
X
θ
)
=
1
σ
2
(
−
y
⊤
X
+
θ
⊤
X
⊤
X
)
∈
R
1
×
D
\begin{aligned} \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} \boldsymbol{\theta}} &=\frac{\mathrm{d}}{\mathrm{d} \boldsymbol{\theta}}\left(\frac{1}{2 \sigma^{2}}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\theta})^{\top}(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{\theta})\right) \\ &=\frac{1}{2 \sigma^{2}} \frac{\mathrm{d}}{\mathrm{d} \boldsymbol{\theta}}\left(\boldsymbol{y}^{\top} \boldsymbol{y}-2 \boldsymbol{y}^{\top} \boldsymbol{X} \boldsymbol{\theta}+\boldsymbol{\theta}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \boldsymbol{\theta}\right) \\ &=\frac{1}{\sigma^{2}}\left(-\boldsymbol{y}^{\top} \boldsymbol{X}+\boldsymbol{\theta}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}\right) \in \mathbb{R}^{1 \times D} \end{aligned}
dθdL=dθd(2σ21(y−Xθ)⊤(y−Xθ))=2σ21dθd(y⊤y−2y⊤Xθ+θ⊤X⊤Xθ)=σ21(−y⊤X+θ⊤X⊤X)∈R1×D
(
d
X
⊤
B
X
d
X
=
(
B
+
B
⊤
)
X
\frac {d\boldsymbol X^\top B\boldsymbol X}{d\boldsymbol X}=(B+B^\top)\boldsymbol X
dXdX⊤BX=(B+B⊤)X)
令上式等于0:
d
L
d
θ
=
0
⊤
⟶
θ
M
L
⊤
X
⊤
X
=
y
⊤
X
⟺
θ
M
L
⊤
=
y
⊤
X
(
X
⊤
X
)
−
1
⟺
θ
M
L
=
(
X
⊤
X
)
−
1
X
⊤
y
.
\begin{aligned} \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} \boldsymbol{\theta}}=\mathbf{0}^{\top} {\longrightarrow} \boldsymbol{\theta}_{\mathrm{ML}}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}=\boldsymbol{y}^{\top} \boldsymbol{X} \\ \Longleftrightarrow \boldsymbol{\theta}_{\mathrm{ML}}^{\top}=\boldsymbol{y}^{\top} \boldsymbol{X}\left(\boldsymbol{X}^{\top} \boldsymbol{X}\right)^{-1} \\ \Longleftrightarrow \boldsymbol{\theta}_{\mathrm{ML}}=\left(\boldsymbol{X}^{\top} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\top} \boldsymbol{y} . \end{aligned}
dθdL=0⊤⟶θML⊤X⊤X=y⊤X⟺θML⊤=y⊤X(X⊤X)−1⟺θML=(X⊤X)−1X⊤y.
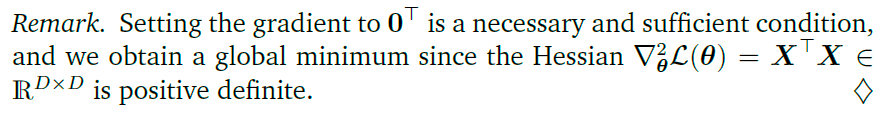
Normal equation is derived by MLE.----Ng
基于特征的极大似然估计(Maximum Likelihood Estimation with Features)
当遇到更复杂的数据时,一次函数模型有时候很难很好地拟合数据,但是由于线性回归模型只是对"参数的线性"(“linear in the parameters”),所以可以在线性回归模型中对非线性模型进行拟合。这就是说我们可以先将输入值进行非线性变换之后,再放到线性模型中。
In Ng’s courses he said this is Linear regression with higher order features. We can alse use SVM to derive new features.
p
(
y
∣
x
,
θ
)
=
N
(
y
∣
ϕ
⊤
(
x
)
θ
,
σ
2
)
⟺
y
=
ϕ
⊤
(
x
)
θ
+
ϵ
=
∑
k
=
0
K
−
1
θ
k
ϕ
k
(
x
)
+
ϵ
p(y|\boldsymbol x,\theta)=\mathcal N(y|\phi^\top(x)\boldsymbol\theta,\sigma^2)\Longleftrightarrow y=\phi^\top(x)\boldsymbol\theta+\epsilon=\sum^{K-1}_{k=0}\theta_k\phi_k(x)+\epsilon
p(y∣x,θ)=N(y∣ϕ⊤(x)θ,σ2)⟺y=ϕ⊤(x)θ+ϵ=k=0∑K−1θkϕk(x)+ϵ
其中,
ϕ
:
R
D
→
R
K
\phi:\mathbb R^D\rightarrow\mathbb R^K
ϕ:RD→RK是一个对
x
x
x的(非)线性变换,
ϕ
k
:
R
D
→
R
\phi_k:\mathbb R^D\rightarrow\mathbb R
ϕk:RD→R是特征向量的第k个分量。
一个实例:
一种对输入数据常用的变换如下
ϕ
(
x
)
=
[
ϕ
0
(
x
)
ϕ
1
(
x
)
⋮
ϕ
K
−
1
(
x
)
]
=
[
1
x
x
2
x
3
⋮
x
K
−
1
]
∈
R
K
\phi(x)=\left[\begin{array}{c} \phi_{0}(x) \\ \phi_{1}(x) \\ \vdots \\ \phi_{K-1}(x) \end{array}\right]=\left[\begin{array}{c} 1 \\ x \\ x^{2} \\ x^{3} \\ \vdots \\ x^{K-1} \end{array}\right] \in \mathbb{R}^{K}
ϕ(x)=⎣⎢⎢⎢⎡ϕ0(x)ϕ1(x)⋮ϕK−1(x)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎡1xx2x3⋮xK−1⎦⎥⎥⎥⎥⎥⎥⎥⎤∈RK
所以:
f
(
x
)
=
∑
k
=
0
K
−
1
θ
k
x
k
=
ϕ
⊤
(
x
)
θ
f(x)=\sum\limits^{K-1}_{k=0}\theta_kx^k=\phi^\top(x)\boldsymbol\theta
f(x)=k=0∑K−1θkxk=ϕ⊤(x)θ
现在看看参数
θ
\theta
θ在线性回归模型下的极大似然估计:
Φ
:
=
[
ϕ
⊤
(
x
1
)
⋮
ϕ
⊤
(
x
N
)
]
=
[
ϕ
0
(
x
1
)
⋯
ϕ
K
−
1
(
x
1
)
ϕ
0
(
x
2
)
⋯
ϕ
K
−
1
(
x
2
)
⋮
⋮
ϕ
0
(
x
N
)
⋯
ϕ
K
−
1
(
x
N
)
]
∈
R
N
×
K
\Phi:=\left[\begin{array}{c} \phi^{\top}\left(x_{1}\right) \\ \vdots \\ \phi^{\top}\left(x_{N}\right) \end{array}\right]=\left[\begin{array}{ccc} \phi_{0}\left(x_{1}\right) & \cdots & \phi_{K-1}\left(x_{1}\right) \\ \phi_{0}\left(x_{2}\right) & \cdots & \phi_{K-1}\left(x_{2}\right) \\ \vdots & & \vdots \\ \phi_{0}\left(x_{N}\right) & \cdots & \phi_{K-1}\left(x_{N}\right) \end{array}\right] \in \mathbb{R}^{N \times K}
Φ:=⎣⎢⎡ϕ⊤(x1)⋮ϕ⊤(xN)⎦⎥⎤=⎣⎢⎢⎢⎡ϕ0(x1)ϕ0(x2)⋮ϕ0(xN)⋯⋯⋯ϕK−1(x1)ϕK−1(x2)⋮ϕK−1(xN)⎦⎥⎥⎥⎤∈RN×K
where
Φ
i
j
=
ϕ
j
(
x
i
)
\Phi_{i j}=\phi_{j}\left(\boldsymbol{x}_{i}\right)
Φij=ϕj(xi) and
ϕ
j
:
R
D
→
R
\phi_{j}: \mathbb{R}^{D} \rightarrow \mathbb{R}
ϕj:RD→R.
这个矩阵被称为特征矩阵(feature matrix)或设计矩阵(design matrix)
有了上面这个矩阵,我们可以将线性回归模型:
p
(
y
∣
x
,
θ
)
=
N
(
y
∣
x
⊤
θ
,
σ
2
)
⇔
y
=
x
⊤
θ
+
ϵ
,
ϵ
∼
N
(
0
,
σ
2
)
p(y|\boldsymbol x,\boldsymbol \theta)=\mathcal N(y|\boldsymbol x^\top\boldsymbol\theta,\sigma^2)\Leftrightarrow y=\boldsymbol x^\top\boldsymbol\theta+\epsilon,\quad \epsilon \sim \mathcal N(0,\sigma^2)
p(y∣x,θ)=N(y∣x⊤θ,σ2)⇔y=x⊤θ+ϵ,ϵ∼N(0,σ2)
从这个式子中可以看出,预测值的结果主要分布于均值的周围
写成:
−
log
p
(
Y
∣
X
,
θ
)
=
1
2
σ
2
(
y
−
Φ
θ
)
⊤
(
y
−
Φ
θ
)
+
const
-\log p(\mathcal Y|\mathcal X,\boldsymbol\theta)=\frac{1}{2\sigma^2}(y-\Phi\boldsymbol\theta)^\top(y-\Phi\boldsymbol\theta)+\operatorname{const}
−logp(Y∣X,θ)=2σ21(y−Φθ)⊤(y−Φθ)+const
将两式子进行比较,发现二者只是将
ϕ
\phi
ϕ欢成了
Φ
\Phi
Φ,所以直接利用模型的结论,得到
θ
\theta
θ的估计值:
θ
M
L
=
(
Φ
⊤
Φ
)
−
1
Φ
⊤
y
\theta_{ML}=(\Phi^\top\Phi)^{-1}\Phi^\top y
θML=(Φ⊤Φ)−1Φ⊤y
需要讨论 Φ \Phi Φ的可逆性
这个是不是支持向量机中的多项式核函数?
( x 1 × x 2 + r ) d (x_1\times x_2 + r)^d (x1×x2+r)d
其中,r为多项式的参数,d为多项式的次数, x 1 、 x 2 x_1、x_2 x1、x2为观测值
噪声方差(Estimating the Noise Variance)
我们之前的讨论都是假定
σ
2
\sigma^2
σ2是已知的,但是实际上可以利用极大似然估计的方式对噪声方差进行估计,所有的步骤与之前一致:
将
p
(
y
∣
x
,
θ
,
σ
2
)
=
1
σ
2
π
e
−
1
2
(
x
−
μ
σ
)
2
p(\mathcal y|\mathcal x,\theta,\sigma^2)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}
p(y∣x,θ,σ2)=σ2π1e−21(σx−μ)2带入到似然函数中:
log
p
(
Y
∣
X
,
θ
,
σ
2
)
=
∑
n
=
1
N
log
N
(
y
n
∣
ϕ
⊤
(
x
n
)
θ
,
σ
2
)
=
∑
n
=
1
N
(
−
1
2
log
(
2
π
)
−
1
2
log
σ
2
−
1
2
σ
2
(
y
n
−
ϕ
⊤
(
x
n
)
θ
)
2
)
=
−
N
2
log
σ
2
−
1
2
σ
2
∑
n
=
1
N
(
y
n
−
ϕ
⊤
(
x
n
)
θ
)
2
⏟
=
:
s
+
const.
\begin{array}{l} \log p\left(\mathcal{Y} \mid \mathcal{X}, \boldsymbol{\theta}, \sigma^{2}\right)=\sum\limits_{n=1}^{N} \log \mathcal{N}\left(y_{n} \mid \phi^{\top}\left(\boldsymbol{x}_{n}\right) \boldsymbol{\theta}, \sigma^{2}\right) \\ =\sum\limits_{n=1}^{N}\left(-\frac{1}{2} \log (2 \pi)-\frac{1}{2} \log \sigma^{2}-\frac{1}{2 \sigma^{2}}\left(y_{n}-\phi^{\top}\left(\boldsymbol{x}_{n}\right) \boldsymbol{\theta}\right)^{2}\right) \\ =-\frac{N}{2} \log \sigma^{2}-\frac{1}{2 \sigma^{2}} \underbrace{\sum_{n=1}^{N}\left(y_{n}-\boldsymbol{\phi}^{\top}\left(\boldsymbol{x}_{n}\right) \boldsymbol{\theta}\right)^{2}}_{=: s}+\text { const. } \end{array}
logp(Y∣X,θ,σ2)=n=1∑NlogN(yn∣ϕ⊤(xn)θ,σ2)=n=1∑N(−21log(2π)−21logσ2−2σ21(yn−ϕ⊤(xn)θ)2)=−2Nlogσ2−2σ21=:s
n=1∑N(yn−ϕ⊤(xn)θ)2+ const.
对
σ
2
\sigma^2
σ2求偏导:
∂
log
p
(
Y
∣
X
,
θ
,
σ
2
)
∂
σ
2
=
−
N
2
σ
2
+
1
2
σ
4
s
=
0
⟺
N
2
σ
2
=
s
2
σ
4
\begin{aligned} & \frac{\partial \log p\left(\mathcal{Y} \mid \mathcal{X}, \boldsymbol{\theta}, \sigma^{2}\right)}{\partial \sigma^{2}}=-\frac{N}{2 \sigma^{2}}+\frac{1}{2 \sigma^{4}} s=0 \\ \Longleftrightarrow & \frac{N}{2 \sigma^{2}}=\frac{s}{2 \sigma^{4}} \end{aligned}
⟺∂σ2∂logp(Y∣X,θ,σ2)=−2σ2N+2σ41s=02σ2N=2σ4s
所以得到
σ
2
\sigma^2
σ2的极大似然估计的结果为:
σ
2
=
s
N
=
1
N
∑
n
−
1
N
(
y
n
−
ϕ
⊤
(
x
n
)
θ
)
2
\sigma^2=\frac{s}{N}=\frac{1}{N}\sum^N_{n-1}(y_n-\phi^\top(\boldsymbol x_n)\theta)^2
σ2=Ns=N1n−1∑N(yn−ϕ⊤(xn)θ)2
the maximum likelihood estimate of the noise variance is the empirical mean of the squared distances between the noise-free function values ϕ ⊤ ( x n ) θ \phi^\top(x_n)\theta ϕ⊤(xn)θand the corresponding noisy observations y n y_n yn at input locations x n x_n xn.
线性回归中的过拟合(Overfitting in Linear Regression)
我们可以使用均方根误差(root mean square error,RMSE)来衡量一个模型的好坏:
1
N
∥
y
−
Φ
θ
∥
2
=
1
N
∑
n
=
1
N
(
y
n
−
ϕ
⊤
(
x
n
)
θ
)
2
\sqrt{\frac{1}{N}\|y-\Phi\boldsymbol\theta\|^2}=\sqrt{\frac{1}{N}\sum^N_{n=1}(y_n-\phi^\top(x_n)\boldsymbol\theta)^2}
N1∥y−Φθ∥2=N1n=1∑N(yn−ϕ⊤(xn)θ)2
噪声参数
σ
2
\sigma^2
σ2不是一个自由模型参数,所以没有直接加到上式,所以没有包含到上面,这样做的好处就是能够使得计算前后的量纲保持一致。
当多项式的次数小于训练样本数量的时候,可以得到一个唯一的极大似然估计值,当大于的时候,需要求解一个欠定方程组(有无穷多解的方程组),这样得到无穷多的估计值。
采用不同级别的多项式模型拟合10个数据的结果如下图:

各个模型的均方根误差:

注意一点,训练集的RMSE不会增加。
极大后验估计(Maximum A Posteriori Estimation)
当出现过拟合的时候,参数的数值会变得很大,为了解决这个问题,我们可以使用先验分布
p
(
θ
)
p(\theta)
p(θ)。这个先验分布标明了参数值在什么范围内是合理的。例如一个高斯先验
p
(
θ
)
=
N
(
0
,
1
)
p(\theta)=\mathcal N(0,1)
p(θ)=N(0,1),这个信息中暗示了参数的范围应该在
[
−
2
,
2
]
[-2,2]
[−2,2]之间(
μ
±
2
σ
\mu\pm2\sigma
μ±2σ).当数据集可用的时候,我们需要去找能够最大化后验分布
p
(
θ
∣
X
,
Y
)
p(\theta|\mathcal X,\mathcal Y)
p(θ∣X,Y)的参数值
θ
\theta
θ,这个过程称为极大后验估计(Maximum a Posteriori Estimation,MAP),后验分布可以利用贝叶斯公式求解:
p
(
θ
∣
X
,
Y
)
=
p
(
Y
∣
X
,
θ
)
p
(
θ
)
p
(
Y
∣
X
)
p(\theta|\mathcal X,\mathcal Y)=\frac{p(\mathcal Y|\mathcal X, \theta)p(\theta)}{p(\mathcal Y|\mathcal X)}
p(θ∣X,Y)=p(Y∣X)p(Y∣X,θ)p(θ)
要求出参数向量
θ
M
A
P
\theta_{MAP}
θMAP,我们需要遵循与极大似然估计一致的方法,首先,先自然对数转换(log-transform):
log
p
(
θ
∣
X
,
Y
)
=
log
p
(
Y
∣
X
,
θ
)
+
log
p
(
θ
)
+
const
\log p(\theta|\mathcal X,\mathcal Y)=\log p(\mathcal Y|\mathcal X,\theta)+\log p(\theta)+\operatorname{const}
logp(θ∣X,Y)=logp(Y∣X,θ)+logp(θ)+const
其中,
const
\operatorname {const}
const中包含独立于
θ
\theta
θ的项。可以看到,后验似然估计是参数先验(在输入数据之前的对参数的认知)和依赖于数据的似然之间的折中。
要求的参数向量,我们要:
θ
M
A
P
∈
arg
min
θ
{
−
log
p
(
Y
∣
X
,
θ
)
−
log
p
(
θ
)
}
\theta_{MAP}\in\arg \min_\theta\{-\log p(\mathcal Y|\mathcal X,\theta)-\log p(\theta)\}
θMAP∈argθmin{−logp(Y∣X,θ)−logp(θ)}
将负对数后验对
θ
\theta
θ进行求导:
−
d
log
p
(
θ
∣
X
,
Y
)
d
θ
=
−
d
log
p
(
Y
∣
X
,
θ
)
d
θ
−
d
log
p
(
θ
)
d
θ
-\frac{\mathrm{d} \log p(\boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y})}{\mathrm{d} \boldsymbol{\theta}}=-\frac{\mathrm{d} \log p(\mathcal{Y} \mid \mathcal{X}, \boldsymbol{\theta})}{\mathrm{d} \theta}-\frac{\mathrm{d} \log p(\boldsymbol{\theta})}{\mathrm{d} \theta}
−dθdlogp(θ∣X,Y)=−dθdlogp(Y∣X,θ)−dθdlogp(θ)
第一项是之前提到的负自然对数似然的梯度:
d L d θ = d d θ ( 1 2 σ 2 ( y − X θ ) ⊤ ( y − X θ ) ) = 1 2 σ 2 d d θ ( y ⊤ y − 2 y ⊤ X θ + θ ⊤ X ⊤ X θ ) = 1 σ 2 ( − y ⊤ X + θ ⊤ X ⊤ X ) ∈ R 1 × D \begin{aligned} \frac{\mathrm{d} \mathcal{L}}{\mathrm{d} \theta} &=\frac{\mathrm{d}}{\mathrm{d} \theta}\left(\frac{1}{2 \sigma^{2}}(y-X \theta)^{\top}(y-X \theta)\right) \\ &=\frac{1}{2 \sigma^{2}} \frac{\mathrm{d}}{\mathrm{d} \theta}\left(y^{\top} y-2 y^{\top} X \theta+\theta^{\top} \boldsymbol{X}^{\top} \boldsymbol{X} \theta\right) \\ &=\frac{1}{\sigma^{2}}\left(-\boldsymbol{y}^{\top} \boldsymbol{X}+\boldsymbol{\theta}^{\top} \boldsymbol{X}^{\top} \boldsymbol{X}\right) \in \mathbb{R}^{1 \times D} \end{aligned} dθdL=dθd(2σ21(y−Xθ)⊤(y−Xθ))=2σ21dθd(y⊤y−2y⊤Xθ+θ⊤X⊤Xθ)=σ21(−y⊤X+θ⊤X⊤X)∈R1×D
利用参数的一个(共轭)高斯先验
p
(
θ
)
=
N
(
0
,
b
2
I
)
p(\theta)=\mathcal N(0,b^2\boldsymbol I)
p(θ)=N(0,b2I):
−
log
p
(
θ
∣
X
,
Y
)
=
1
2
σ
2
(
y
−
Φ
θ
)
⊤
(
y
−
Φ
θ
)
+
1
2
b
2
θ
⊤
θ
+
const
-\log p(\theta \mid \mathcal{X}, \mathcal{Y})=\frac{1}{2 \sigma^{2}}(y-\Phi \theta)^{\top}(y-\Phi \theta)+\frac{1}{2 b^{2}} \theta^{\top} \theta+\text { const }
−logp(θ∣X,Y)=2σ21(y−Φθ)⊤(y−Φθ)+2b21θ⊤θ+ const
这里有点疑问,利用了
p ( y ∣ x , θ ) = N ( y ∣ ϕ ⊤ ( x ) θ , σ 2 ) ⟺ y = ϕ ⊤ ( x ) θ + ϵ = ∑ k = 0 K − 1 θ k ϕ k ( x ) + ϵ p(y|\boldsymbol x,\theta)=\mathcal N(y|\phi^\top(x)\boldsymbol\theta,\sigma^2)\Longleftrightarrow y=\phi^\top(x)\boldsymbol\theta+\epsilon=\sum^{K-1}_{k=0}\theta_k\phi_k(x)+\epsilon p(y∣x,θ)=N(y∣ϕ⊤(x)θ,σ2)⟺y=ϕ⊤(x)θ+ϵ=k=0∑K−1θkϕk(x)+ϵ
??
上式右边的第一个式子来源于自然对数似然,第二个式子来源于自然对数先验。所以自然对数先验对
θ
\theta
θ的先验为:
−
d
log
p
(
θ
∣
X
,
Y
)
d
θ
=
1
σ
2
(
θ
⊤
Φ
⊤
Φ
−
y
⊤
Φ
)
+
1
b
2
θ
⊤
-\frac{d\log p(\theta|\mathcal X,\mathcal Y)}{d\theta}=\frac{1}{\sigma^2}(\theta^\top\Phi^\top\Phi-y^\top\Phi)+\frac{1}{b^2}\theta^\top
−dθdlogp(θ∣X,Y)=σ21(θ⊤Φ⊤Φ−y⊤Φ)+b21θ⊤
将梯度设置为0:
1
σ
2
(
θ
⊤
Φ
⊤
Φ
−
y
⊤
Φ
)
+
1
b
2
θ
⊤
=
0
⊤
⟺
θ
⊤
(
1
σ
2
Φ
⊤
Φ
+
1
b
2
I
)
−
1
σ
2
y
⊤
Φ
=
0
⊤
⟺
θ
⊤
(
Φ
⊤
Φ
+
σ
2
b
2
I
)
=
y
⊤
Φ
⟺
θ
⊤
=
y
⊤
Φ
(
Φ
⊤
Φ
+
σ
2
b
2
I
)
−
1
\begin{aligned} & \frac{1}{\sigma^{2}}\left(\theta^{\top} \Phi^{\top} \Phi-y^{\top} \Phi\right)+\frac{1}{b^{2}} \theta^{\top}=0^{\top} \\ \Longleftrightarrow & \theta^{\top}\left(\frac{1}{\sigma^{2}} \Phi^{\top} \Phi+\frac{1}{b^{2}} I\right)-\frac{1}{\sigma^{2}} y^{\top} \Phi=0^{\top} \\ \Longleftrightarrow & \theta^{\top}\left(\Phi^{\top} \Phi+\frac{\sigma^{2}}{b^{2}} I\right)=y^{\top} \Phi \\ \Longleftrightarrow & \theta^{\top}=y^{\top} \Phi\left(\Phi^{\top} \Phi+\frac{\sigma^{2}}{b^{2}} I\right)^{-1} \end{aligned}
⟺⟺⟺σ21(θ⊤Φ⊤Φ−y⊤Φ)+b21θ⊤=0⊤θ⊤(σ21Φ⊤Φ+b21I)−σ21y⊤Φ=0⊤θ⊤(Φ⊤Φ+b2σ2I)=y⊤Φθ⊤=y⊤Φ(Φ⊤Φ+b2σ2I)−1
整理得:
θ
M
A
P
=
(
Φ
⊤
Φ
+
σ
2
b
2
I
)
−
1
Φ
⊤
y
\theta_{MAP}=(\Phi^\top\Phi+\frac{\sigma^2}{b^2}I)^{-1}\Phi^\top y
θMAP=(Φ⊤Φ+b2σ2I)−1Φ⊤y
与极大似然估计的结果:
θ
M
L
=
(
Φ
⊤
Φ
)
−
1
Φ
⊤
y
\theta_{ML}=(\Phi^\top\Phi)^{-1}\Phi^\top y
θML=(Φ⊤Φ)−1Φ⊤y相比较,只是在逆当中多了一项
σ
2
b
2
I
\frac{\sigma^2}{b^2}I
b2σ2I,这一项保证了
Φ
⊤
Φ
+
σ
2
b
2
I
\Phi^\top\Phi+\frac{\sigma^2}{b^2}I
Φ⊤Φ+b2σ2I是一个对称严格正定的。也就是说这个矩阵是可逆的,而且是线性方程的唯一解。同时他也反应了正则项(regularizer)的影响的大小
虽然先验能够让高次多项式变得更加光滑,但也是仅仅将过拟合的边界向后推移了,想要解决过拟合的问题需要其他的方法。
极大后验估计作为正则化
带正则项的最小二乘的损失函数为:
∥
y
−
Φ
θ
∥
2
+
λ
∥
θ
∥
2
2
\|\boldsymbol y-\boldsymbol\Phi\boldsymbol\theta\|^2+\lambda\|\boldsymbol\theta\|_2^2
∥y−Φθ∥2+λ∥θ∥22
这里的范数采用的是 p p p-范数,当 p p p的值越小,得到的结果中 θ = 0 \theta=0 θ=0的个数就越多。当 p = 1 p=1 p=1时,被称为最小绝对收缩和选择算子(least absolute shrinkage and selection operator,LASSO)
上式中的正则项可以理解为极大后验估计中的高斯自然对数先验(negative log-Gaussian prior),具体来说,对于一个正态分布
p
(
θ
)
=
N
(
0
,
b
2
I
)
p(\boldsymbol\theta)=\mathcal N(\boldsymbol0,b^2\boldsymbol I)
p(θ)=N(0,b2I)的高斯自然对数先验为:
−
log
p
(
θ
)
=
1
2
b
2
∥
θ
∥
2
2
+
const
-\log p(\boldsymbol\theta)=\frac{1}{2b^2}\|\boldsymbol \theta\|^2_2+\operatorname{const}
−logp(θ)=2b21∥θ∥22+const
这里的正则项为
1
2
b
2
\frac{1}{2b^2}
2b21与极大后验估计的先验一致。这样看来,正则化后的最小二乘损失函数包含的项与负自然对数似然和负自然对数先验有紧密关系,所以最小化最小二乘损失函数的过程与极大后验估计一致.
最小化带正则项的最小二乘损失函数(regularized least-squares loss function):
θ
R
L
S
=
(
Φ
⊤
Φ
+
λ
I
)
−
1
Φ
⊤
y
\boldsymbol\theta_{RLS}=(\boldsymbol\Phi^\top\boldsymbol\Phi+\lambda \boldsymbol I)^{-1}\boldsymbol\Phi^\top \boldsymbol y
θRLS=(Φ⊤Φ+λI)−1Φ⊤y
这个与极大后验估计一致,这里的正则项为
λ
=
σ
2
b
2
\lambda=\frac{\sigma^2}{b^2}
λ=b2σ2,其中,
σ
2
\sigma^2
σ2是噪声方差,
b
2
b^2
b2为(各向同性)高斯先验方差
p
(
θ
)
=
N
(
0
,
b
2
I
)
p(\boldsymbol\theta)=\mathcal N(\boldsymbol0,b^2\boldsymbol I)
p(θ)=N(0,b2I)
至此,我们讨论的都是点估计得到
θ
∗
\theta^*
θ∗,以对目标函数进行优化。接下来我们讨论使用贝叶斯推断,通过获得所有合理的参数的均值得到优化结果。
贝叶斯线性回归(Bayesian Linear Regression)
先前讨论的是采用极大似然估计和极大后验估计来估计模型的参数,极大似然估计容易出现过拟合的现象,尤其是在训练集比较小的时候。极大后验估计使用一个概率先验来解决这个问题。而贝叶斯回归不求出单一的参数,而是选择求所有合理的参数的均值。
模型(Model)
p
r
i
o
r
p
(
θ
)
=
N
(
m
0
,
S
0
)
l
i
k
e
l
i
h
o
o
d
p
(
y
∣
x
,
θ
)
=
(
y
∣
ϕ
⊤
(
x
)
θ
,
σ
)
\begin{aligned}&prior \quad p(\boldsymbol\theta)=\mathcal N(\boldsymbol m_0,\boldsymbol S_0)\\ & likelihood\quad p(y|\boldsymbol x,\boldsymbol\theta)=\mathcal (y|\phi^\top(x)\boldsymbol\theta,\sigma)\end{aligned}
priorp(θ)=N(m0,S0)likelihoodp(y∣x,θ)=(y∣ϕ⊤(x)θ,σ)
对应的图模型:
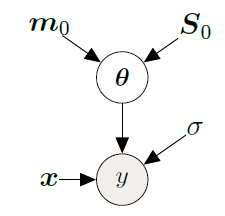
已观测变量与未观测变量的联合概率分布为:
p
(
y
,
θ
∣
x
)
=
p
(
y
∣
θ
,
x
)
p
(
θ
)
p(y,\boldsymbol\theta|x)=p(y|\theta,x)p(\boldsymbol\theta)
p(y,θ∣x)=p(y∣θ,x)p(θ)
推导过程
p ( y , θ ∣ x ) = p ( y ∣ θ , x ) p ( θ , x ) p ( x ) = p ( y ∣ θ , x ) ⋅ p ( θ ∣ x ) p(y,\theta|x)=\frac{p(y|\theta,x)p(\theta ,x)}{p(x)}=p(y|\theta,x)\cdot p(\theta|x) p(y,θ∣x)=p(x)p(y∣θ,x)p(θ,x)=p(y∣θ,x)⋅p(θ∣x)
所以x与 θ \theta θ是相互独立的?应该是 θ \theta θ与验证数据无关
预测先验(Prior Predictions)
预测的最终目的不是获得模型的参数,而是获得预测值,在贝叶斯回归中,预测值是所有合理参数的预测值的均值:
p
(
y
∗
∣
x
∗
)
=
∫
p
(
y
∗
∣
x
∗
,
θ
)
p
(
θ
)
d
θ
=
E
θ
[
p
(
y
∗
∣
x
∗
,
θ
)
]
p(y_*|x_*)=\int p(y_*|\boldsymbol x_*,\boldsymbol\theta)p(\boldsymbol\theta)d\boldsymbol\theta=\mathbb E_\theta[p(y_*|\boldsymbol x_*,\boldsymbol\theta)]
p(y∗∣x∗)=∫p(y∗∣x∗,θ)p(θ)dθ=Eθ[p(y∗∣x∗,θ)]
连续概率分布的均值,样品值乘以样品出现的概率,将他们之和加起来,得到均值
我们选取一个
θ
\theta
θ的(共轭)高斯先验作为模型,于是可以知道预测结果也是高斯分布,对于一个先验分布
p
(
θ
)
=
N
(
m
0
,
S
0
)
p(\boldsymbol\theta)=\mathcal N(\boldsymbol m_0,\boldsymbol S_0)
p(θ)=N(m0,S0),对应的预测结果的分布为:
p
(
y
∗
∣
x
∗
)
=
N
(
ϕ
⊤
(
x
∗
)
m
0
,
ϕ
⊤
(
x
∗
)
S
0
ϕ
(
x
∗
)
+
σ
2
)
p(y_*|\boldsymbol x_*)=\mathcal N(\boldsymbol\phi^\top(\boldsymbol x_*)\boldsymbol m_0,\phi^\top(\boldsymbol x_*)\boldsymbol S_0\phi(\boldsymbol x_*)+\sigma^2)
p(y∗∣x∗)=N(ϕ⊤(x∗)m0,ϕ⊤(x∗)S0ϕ(x∗)+σ2)
贝叶斯回归模型为:
p ( θ ) = N ( m 0 , S 0 ) p ( y ∣ x , θ ) = N ( y ∣ ϕ ⊤ θ , σ 2 ) p(\theta) =\mathcal N(m_0,S_0)\\ p(y|x,\theta)=\mathcal N(y|\phi^\top\theta,\sigma^2) p(θ)=N(m0,S0)p(y∣x,θ)=N(y∣ϕ⊤θ,σ2)
x与y的对应关系为: y ∗ = ϕ ⊤ ( x ∗ ) θ y^*=\phi^\top(x^*)\theta y∗=ϕ⊤(x∗)θ
所以对应y的均值为: ϕ ⊤ m 0 \phi^\top m_0 ϕ⊤m0
由 V Y [ y ] = V X [ A x + b ] = V X [ A x ] = A V X A ⊤ = A Σ A ⊤ \mathbb V_Y[y]=\mathbb V_X[Ax+b]=\mathbb V_X[Ax]=A\mathbb V_X A^\top=A\Sigma A^\top VY[y]=VX[Ax+b]=VX[Ax]=AVXA⊤=AΣA⊤:
y的对应的方差为: ϕ ⊤ ( x ∗ ) S 0 ϕ ( x ∗ ) \phi^\top(x_*)S_0\phi(x_*) ϕ⊤(x∗)S0ϕ(x∗),加上噪声项即为上式
上式中的
σ
2
\sigma^2
σ2是由于测量误差导致的不确定分布。
这里预测值是高斯分布是因为高斯共轭和边际化的性质。由于高斯噪音是相互独立的,所以:
V
[
y
∗
]
=
V
θ
[
ϕ
⊤
(
x
∗
)
θ
]
+
V
ϵ
[
ϵ
]
\mathbb V[y_*]=\mathbb V_\boldsymbol\theta[\phi^\top(x_*)\boldsymbol\theta]+\mathbb V_\epsilon[\epsilon]
V[y∗]=Vθ[ϕ⊤(x∗)θ]+Vϵ[ϵ]
如果我们考虑无噪音函数:
f
(
x
∗
)
=
ϕ
⊤
(
x
∗
)
θ
f(\boldsymbol x_*)=\phi^\top(x_*)\boldsymbol\theta
f(x∗)=ϕ⊤(x∗)θ
p
(
f
(
x
∗
)
)
=
N
(
ϕ
⊤
(
x
∗
)
m
0
,
ϕ
⊤
(
x
∗
)
S
0
ϕ
(
x
∗
)
)
p(f(x_*))=\mathcal N(\phi^\top(x_*)m_0,\phi^\top(x_*)S_0\phi(x_*))
p(f(x∗))=N(ϕ⊤(x∗)m0,ϕ⊤(x∗)S0ϕ(x∗))
这个式子与原先式子不同之处在于少了噪音项
σ
2
\sigma^2
σ2
函数分布(Distribution over Functions):
我们可以用一系列的参数
θ
i
\theta_i
θi表示参数分布
p
(
θ
)
p(\boldsymbol\theta)
p(θ),而每一个参数对应一个函数
f
(
⋅
)
=
θ
i
⊤
ϕ
(
⋅
)
f(\cdot)=\boldsymbol\theta^\top_i\phi(\cdot)
f(⋅)=θi⊤ϕ(⋅)于是可以得到对应函数的分布
p
(
f
(
⋅
)
)
p(f(\cdot))
p(f(⋅))
p305 没弄清楚
置信区间和置信边界
后验分布(Posterior Distribution)
利用贝叶斯公式可以计算参数的后验分布:
p
(
θ
∣
X
,
Y
)
=
p
(
Y
∣
X
,
θ
)
p
(
θ
)
p
(
Y
∣
X
)
p(\theta|\mathcal X,\mathcal Y)=\frac{p(\mathcal Y|\mathcal X, \theta)p(\theta)}{p(\mathcal Y|\mathcal X)}
p(θ∣X,Y)=p(Y∣X)p(Y∣X,θ)p(θ)
其中
X
\mathcal X
X是训练的输入值,
Y
\mathcal Y
Y是训练目标。
其中的边际似然(marginal likelihood/evidence)与参数无关:
p
(
Y
∣
X
)
=
∫
p
(
Y
∣
X
,
θ
)
p
(
θ
)
d
θ
=
E
θ
[
p
(
Y
∣
X
,
θ
)
]
p(\mathcal Y|\mathcal X)=\int p(\mathcal Y|\mathcal X, \theta)p(\theta)d\theta=\mathbb E_\theta[p(\mathcal Y|\mathcal X,\theta)]
p(Y∣X)=∫p(Y∣X,θ)p(θ)dθ=Eθ[p(Y∣X,θ)]
边际似然可以被看成是所有合理参数下预测值的均值。
参数后验:
p
(
θ
∣
X
,
Y
)
=
N
(
θ
∣
m
N
,
S
N
)
S
N
=
(
S
0
−
1
+
σ
−
2
Φ
⊤
Φ
)
−
1
m
N
=
S
N
(
S
0
−
1
m
0
+
σ
−
2
Φ
⊤
y
)
\begin{aligned}p(\boldsymbol\theta|\mathcal X, \mathcal Y) & =\mathcal N(\boldsymbol\theta |\boldsymbol m_N,\boldsymbol S_N)\\ \boldsymbol S_N &=(\boldsymbol S_0^{-1}{+\sigma^{-2}}\Phi^\top\Phi)^{-1}\\\boldsymbol m_N&=\boldsymbol S_N(\boldsymbol S_0^{-1}\boldsymbol m_0+\sigma^{-2}\Phi^\top \boldsymbol y)\end{aligned}
p(θ∣X,Y)SNmN=N(θ∣mN,SN)=(S0−1+σ−2Φ⊤Φ)−1=SN(S0−1m0+σ−2Φ⊤y)
其中的N代表的是训练集的大小。
证明:
证明思路类似是用两种方式将参数后验表示出来,然后将对应部分的进行对比,得到想要的参数。
由贝叶斯公式可以得知,后验概率分布与似然概率分布和先验概率分布成比例
Posterior
p
(
θ
∣
X
,
Y
)
=
p
(
Y
∣
X
,
θ
)
p
(
θ
)
p
(
Y
∣
X
)
Likelihood
p
(
Y
∣
X
,
θ
)
=
N
(
y
∣
Φ
θ
,
σ
2
I
)
Prior
p
(
θ
)
=
N
(
θ
∣
m
0
,
S
0
)
\begin{array}{ll} \text { Posterior } & p(\boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y})=\frac{p(\mathcal{Y} \mid \mathcal{X}, \boldsymbol{\theta}) p(\boldsymbol{\theta})}{p(\mathcal{Y} \mid \mathcal{X})} \\ \text { Likelihood } & p(\mathcal{Y} \mid \mathcal{X}, \boldsymbol{\theta})=\mathcal{N}\left(\boldsymbol{y} \mid \boldsymbol{\Phi} \boldsymbol{\theta}, \sigma^{2} \boldsymbol{I}\right) \\ \text { Prior } & p(\boldsymbol{\theta})=\mathcal{N}\left(\boldsymbol{\theta} \mid \boldsymbol{m}_{0}, \boldsymbol{S}_{0}\right) \end{array}
Posterior Likelihood Prior p(θ∣X,Y)=p(Y∣X)p(Y∣X,θ)p(θ)p(Y∣X,θ)=N(y∣Φθ,σ2I)p(θ)=N(θ∣m0,S0)
现在考虑自然对数先验与自然对数似然之和:
log
N
(
y
∣
Φ
θ
,
σ
2
I
)
+
log
N
(
θ
∣
m
0
,
S
0
)
=
−
1
2
(
σ
−
2
(
y
−
Φ
θ
)
⊤
(
y
−
Φ
θ
)
+
(
θ
−
m
0
)
⊤
S
0
−
1
(
θ
−
m
0
)
)
+
const
\begin{aligned}&\log \mathcal N(y|\Phi\theta,\sigma^2 I)+\log \mathcal N(\theta|m_0,S_0)\\&=-\frac{1}{2}(\sigma^{-2}(y-\Phi\theta)^\top(y-\Phi\theta)+(\theta-m_0)^\top S_0^{-1}(\theta-m_0))+\operatorname{const}\end{aligned}
logN(y∣Φθ,σ2I)+logN(θ∣m0,S0)=−21(σ−2(y−Φθ)⊤(y−Φθ)+(θ−m0)⊤S0−1(θ−m0))+const
其中的const包含一些独立于
θ
\theta
θ的项。
将上式进行展开:(将式子中的二次项一次项进行整合)
−
1
2
(
σ
−
2
y
⊤
y
−
2
σ
−
2
y
⊤
Φ
θ
+
θ
⊤
σ
−
2
Φ
⊤
Φ
θ
+
θ
⊤
S
0
−
1
θ
−
2
m
0
⊤
S
0
−
1
θ
+
m
0
⊤
S
0
−
1
m
0
)
=
−
1
2
(
θ
⊤
(
σ
−
2
Φ
⊤
Φ
+
S
0
−
1
)
θ
−
2
(
σ
−
2
Φ
⊤
y
+
S
0
−
1
m
0
)
⊤
θ
)
+
c
o
n
s
t
\begin{aligned} &-\frac{1}{2}\left(\sigma^{-2} \boldsymbol{y}^{\top} \boldsymbol{y}-2 \sigma^{-2} \boldsymbol{y}^{\top} \Phi \theta+\boldsymbol{\theta}^{\top} \sigma^{-2} \boldsymbol{\Phi}^{\top} \boldsymbol{\Phi} \boldsymbol{\theta}+\boldsymbol{\theta}^{\top} \boldsymbol{S}_{0}^{-1} \boldsymbol{\theta}\right.\\ &\left.-2 m_{0}^{\top} S_{0}^{-1} \theta+\boldsymbol{m}_{0}^{\top} \boldsymbol{S}_{0}^{-1} \boldsymbol{m}_{0}\right) \\ =&-\frac{1}{2}\left(\boldsymbol{\theta}^{\top}\left(\sigma^{-2} \boldsymbol{\Phi}^{\top} \boldsymbol{\Phi}+\boldsymbol{S}_{0}^{-1}\right) \boldsymbol{\theta}-2\left(\sigma^{-2} \Phi^{\top} y+S_{0}^{-1} m_{0}\right)^{\top} \theta\right)+\mathrm{const} \end{aligned}
=−21(σ−2y⊤y−2σ−2y⊤Φθ+θ⊤σ−2Φ⊤Φθ+θ⊤S0−1θ−2m0⊤S0−1θ+m0⊤S0−1m0)−21(θ⊤(σ−2Φ⊤Φ+S0−1)θ−2(σ−2Φ⊤y+S0−1m0)⊤θ)+const
我们可以发现上式与
θ
\theta
θ呈二次关系。
The fact that the unnormalized log-posterior distribution is a (negative) quadratic form implies that the posterior is Gaussian
p
(
θ
∣
X
,
Y
)
=
exp
(
log
p
(
θ
∣
X
,
Y
)
)
∝
exp
(
log
p
(
Y
∣
X
,
θ
)
+
log
p
(
θ
)
)
∝
exp
(
−
1
2
(
θ
⊤
(
σ
−
2
Φ
⊤
Φ
+
S
0
−
1
)
θ
−
2
(
σ
−
2
Φ
⊤
y
+
S
0
−
1
m
0
)
⊤
θ
)
)
p(\theta|\mathcal X,\mathcal Y)=\exp(\log p(\theta|\mathcal X,\mathcal Y))\propto \exp(\log p(\mathcal Y|\mathcal X,\theta)+\log p(\theta))\\ \propto \exp(-\frac{1}{2}(\theta^\top(\sigma^{-2}\Phi^\top\Phi+S_0^{-1})\theta-2(\sigma^{-2}\Phi^\top y+S_0^{-1}m_0)^\top \theta))
p(θ∣X,Y)=exp(logp(θ∣X,Y))∝exp(logp(Y∣X,θ)+logp(θ))∝exp(−21(θ⊤(σ−2Φ⊤Φ+S0−1)θ−2(σ−2Φ⊤y+S0−1m0)⊤θ))
最后需要从上式中找到均值和方差矩阵(
N
(
θ
∣
m
N
,
S
N
)
\mathcal N(\theta|m_N,S_N)
N(θ∣mN,SN)):
log
N
(
θ
∣
m
N
,
S
N
)
=
−
1
2
(
θ
−
m
N
)
⊤
S
N
−
1
(
θ
−
m
N
)
+
c
o
n
s
t
=
−
1
2
(
θ
⊤
S
N
−
1
θ
−
2
m
N
⊤
S
N
−
1
θ
+
m
N
⊤
S
N
−
1
m
N
)
\log \mathcal{N}\left(\boldsymbol{\theta} \mid \boldsymbol{m}_{N}, \boldsymbol{S}_{N}\right)=-\frac{1}{2}\left(\boldsymbol{\theta}-\boldsymbol{m}_{N}\right)^{\top} \boldsymbol{S}_{N}^{-1}\left(\boldsymbol{\theta}-\boldsymbol{m}_{N}\right)+ const\\=-\frac{1}{2}\left(\theta^{\top} S_{N}^{-1} \theta-2 m_{N}^{\top} S_{N}^{-1} \theta+\boldsymbol{m}_{N}^{\top} \boldsymbol{S}_{N}^{-1} \boldsymbol{m}_{N}\right)
logN(θ∣mN,SN)=−21(θ−mN)⊤SN−1(θ−mN)+const=−21(θ⊤SN−1θ−2mN⊤SN−1θ+mN⊤SN−1mN)
通过比较上面二式可以得到:
S
N
−
1
=
Φ
⊤
σ
−
2
I
Φ
+
S
0
−
1
⟺
S
N
=
(
σ
−
2
Φ
⊤
Φ
+
S
0
−
1
)
−
1
m
N
⊤
S
N
−
1
=
(
σ
−
2
Φ
⊤
y
+
S
0
−
1
m
0
)
⊤
⟺
m
N
=
S
N
(
σ
−
2
Φ
⊤
y
+
S
0
−
1
m
0
)
\begin{array}{c} S_{N}^{-1}=\Phi^{\top} \sigma^{-2} \boldsymbol{I} \Phi+S_{0}^{-1} \\ \Longleftrightarrow \boldsymbol{S}_{N}=\left(\sigma^{-2} \boldsymbol{\Phi}^{\top} \boldsymbol{\Phi}+\boldsymbol{S}_{0}^{-1}\right)^{-1} \\ \\ \boldsymbol{m}_{N}^{\top} \boldsymbol{S}_{N}^{-1}=\left(\sigma^{-2} \boldsymbol{\Phi}^{\top} \boldsymbol{y}+\boldsymbol{S}_{0}^{-1} \boldsymbol{m}_{0}\right)^{\top} \\ \Longleftrightarrow \boldsymbol{m}_{N}=\boldsymbol{S}_{N}\left(\sigma^{-2} \boldsymbol{\Phi}^{\top} \boldsymbol{y}+\boldsymbol{S}_{0}^{-1} \boldsymbol{m}_{0}\right) \end{array}
SN−1=Φ⊤σ−2IΦ+S0−1⟺SN=(σ−2Φ⊤Φ+S0−1)−1mN⊤SN−1=(σ−2Φ⊤y+S0−1m0)⊤⟺mN=SN(σ−2Φ⊤y+S0−1m0)
完全平方的一般方法(General Approach to Completing the Squares)
对于一个等式( A A A是一个堆成正定矩阵):
x ⊤ A ⊤ x − 2 a ⊤ x + c o n s t 1 x^\top A^\top x-2a^\top x+const_1 x⊤A⊤x−2a⊤x+const1
可以得到:
( x − μ ) ⊤ Σ ( x − μ ) + c o n s t 2 (x-\mu)^\top \Sigma(x-\mu)+const_2 (x−μ)⊤Σ(x−μ)+const2
其中, Σ : = A ; μ : = Σ − 1 a ; c o n s t 2 = c o n s t 1 − μ ⊤ Σ μ \Sigma := A;\mu := \Sigma^{-1}a;const_2 = const_1-\mu^\top\Sigma\mu Σ:=A;μ:=Σ−1a;const2=const1−μ⊤Σμ
这部分需要补充
后验预测(Posterior Predictions)
p
(
y
∗
∣
X
,
Y
,
x
∗
)
=
∫
p
(
y
∗
∣
x
∗
,
θ
)
p
(
θ
∣
X
,
Y
)
d
θ
=
∫
N
(
y
∗
∣
ϕ
⊤
(
x
∗
)
θ
,
σ
2
)
N
(
θ
∣
m
N
,
S
N
)
d
θ
=
N
(
y
∗
∣
ϕ
⊤
(
x
∗
)
m
N
,
ϕ
⊤
(
x
∗
)
S
N
ϕ
(
x
∗
)
+
σ
2
)
\begin{aligned} p\left(y_{*} \mid \mathcal{X}, \mathcal{Y}, \boldsymbol{x}_{*}\right) &=\int p\left(y_{*} \mid \boldsymbol{x}_{*}, \boldsymbol{\theta}\right) p(\boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y}) \mathrm{d} \boldsymbol{\theta} \\ &=\int \mathcal{N}\left(y_{*} \mid \phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{\theta}, \sigma^{2}\right) \mathcal{N}\left(\boldsymbol{\theta} \mid \boldsymbol{m}_{N}, \boldsymbol{S}_{N}\right) \mathrm{d} \boldsymbol{\theta} \\ &=\mathcal{N}\left(y_{*} \mid \phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{m}_{N}, \boldsymbol{\phi}^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{S}_{N} \phi\left(\boldsymbol{x}_{*}\right)+\sigma^{2}\right) \end{aligned}
p(y∗∣X,Y,x∗)=∫p(y∗∣x∗,θ)p(θ∣X,Y)dθ=∫N(y∗∣ϕ⊤(x∗)θ,σ2)N(θ∣mN,SN)dθ=N(y∗∣ϕ⊤(x∗)mN,ϕ⊤(x∗)SNϕ(x∗)+σ2)
右式中的第一个分布式利用训练得到的参数和输入值计算之后得到的结果的分布(
y
∗
=
ϕ
(
x
∗
)
θ
y^*=\phi(x^*)\theta
y∗=ϕ(x∗)θ),第二个分布是用训练集训练得到的参数
θ
\theta
θ,
ϕ
⊤
(
x
∗
)
S
N
ϕ
(
x
∗
)
\phi^\top(x_*)S_N\phi(x_*)
ϕ⊤(x∗)SNϕ(x∗)表示关于后验的不确定性.
上式可以等价地写成
E
θ
∣
X
,
Y
[
p
(
y
∗
∣
x
∗
,
θ
)
]
\mathbb E_{\theta|\mathcal X,\mathcal Y}[p(y_*|x_*,\theta)]
Eθ∣X,Y[p(y∗∣x∗,θ)]
分布方程(Distribution over Functions)
当我们使用积分将参数 θ \theta θ消掉时,我们得到了一个分布函数:如果我们从 θ i ∼ p ( θ ∣ X , Y ) \theta_i \sim p(\theta|\mathcal X, \mathcal Y) θi∼p(θ∣X,Y)中取样,我们可以得到方程 θ i ⊤ ϕ ( ⋅ ) \theta^\top_i\phi(\cdot) θi⊤ϕ(⋅)。均值方程为所有预测值的期望 E θ [ f ( ⋅ ) ∣ θ , X , Y ] = m N ⊤ ϕ ( ⋅ ) \mathbb E_\theta[f(\cdot)|\theta,\mathcal X,\mathcal Y]=m^\top_N\phi(\cdot) Eθ[f(⋅)∣θ,X,Y]=mN⊤ϕ(⋅),函数的方差为 ϕ ⊤ ( ⋅ ) S N ϕ ( ⋅ ) \phi^\top(\cdot) S_N\phi(\cdot) ϕ⊤(⋅)SNϕ(⋅)
从 p ( θ ) = N ( 0 , 1 4 I ) p(\theta)=\mathcal N(0,\frac14I) p(θ)=N(0,41I)中对参数进行抽样,表示为第三张图:
无噪音函数值的均值和方差(Mean and Variance of Noise-Free Function Values)
在很多情况下,我们并不关心(含噪音的)预测值的分布 p ( y ∗ ∣ X , Y , x ∗ ) p(y_*|\mathcal X, \mathcal Y,x_*) p(y∗∣X,Y,x∗)。我们更关注于无噪音的函数值 f ( x ∗ ) = ϕ ⊤ ( x ∗ ) θ f(x_*)=\phi^\top(x_*)\theta f(x∗)=ϕ⊤(x∗)θ,可以得到该函数的均值和方差:
E [ f ( x ∗ ) ∣ X , Y ] = E θ [ ϕ ⊤ ( x ∗ ) θ ∣ X , Y ] = ϕ ⊤ ( x ∗ ) E θ [ θ ∣ X , Y ] = ϕ ⊤ ( x ∗ ) m N = m N ⊤ ϕ ( x ∗ ) , V θ [ f ( x ∗ ) ∣ X , Y ] = V θ [ ϕ ⊤ ( x ∗ ) θ ∣ X , Y ] = ϕ ⊤ ( x ∗ ) V θ [ θ ∣ X , Y ] ϕ ( x ∗ ) = ϕ ⊤ ( x ∗ ) S N ϕ ( x ∗ ) \begin{aligned} \mathbb{E}\left[f\left(\boldsymbol{x}_{*}\right) \mid \mathcal{X}, \mathcal{Y}\right]=& \mathbb{E}_{\boldsymbol{\theta}}\left[\phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y}\right]=\phi^{\top}\left(\boldsymbol{x}_{*}\right) \mathbb{E}_{\boldsymbol{\theta}}[\boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y}] \\ &=\phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{m}_{N}=\boldsymbol{m}_{N}^{\top} \phi\left(\boldsymbol{x}_{*}\right), \\ \mathbb{V}_{\boldsymbol{\theta}}\left[f\left(\boldsymbol{x}_{*}\right) \mid \mathcal{X}, \mathcal{Y}\right] &=\mathbb{V}_{\boldsymbol{\theta}}\left[\phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y}\right] \\ &=\phi^{\top}\left(\boldsymbol{x}_{*}\right) \mathbb{V}_{\boldsymbol{\theta}}[\boldsymbol{\theta} \mid \mathcal{X}, \mathcal{Y}] \phi\left(\boldsymbol{x}_{*}\right) \\ &=\phi^{\top}\left(\boldsymbol{x}_{*}\right) \boldsymbol{S}_{N} \phi\left(\boldsymbol{x}_{*}\right) \end{aligned} E[f(x∗)∣X,Y]=Vθ[f(x∗)∣X,Y]Eθ[ϕ⊤(x∗)θ∣X,Y]=ϕ⊤(x∗)Eθ[θ∣X,Y]=ϕ⊤(x∗)mN=mN⊤ϕ(x∗),=Vθ[ϕ⊤(x∗)θ∣X,Y]=ϕ⊤(x∗)Vθ[θ∣X,Y]ϕ(x∗)=ϕ⊤(x∗)SNϕ(x∗)
我们可以发现均值与含噪音观测的均值一致,因为噪音的均值为0,因为噪音的方差为 σ 2 \sigma^2 σ2,所以当预测含噪音的函数值时,需要加上,无噪音的时候则不需要。
还是没能很好地理解噪音这个概念

上图是由参数后验得到的后验分布。由上图可知,当多项式为低阶的时候,参数的分布不会很分散。而对于高阶的贝叶斯回归模型,后验概率的不确定性很大,这个信息对于决策系统(decision-making system)很重要。
边际似然的计算(Computing the Marginal Likelihood)
在本节中,我们介绍参数为共轭高斯先验的贝叶斯线性回归的边际似然的计算。
考虑以下参数形成的过程:
θ
∼
N
(
m
0
,
S
0
)
y
n
∣
x
n
,
θ
∼
N
(
x
n
⊤
θ
,
σ
2
)
,
n
=
1
,
…
,
N
\begin{aligned}\theta&\sim \mathcal N(m_0,S_0)\\y_n|x_n, \theta&\sim\mathcal N(x_n^\top\theta,\sigma^2),\quad n=1,\dots,N\end{aligned}
θyn∣xn,θ∼N(m0,S0)∼N(xn⊤θ,σ2),n=1,…,N
则对应的边际似然为:
p
(
Y
∣
X
)
=
∫
p
(
Y
∣
X
,
θ
)
p
(
θ
)
d
θ
=
∫
N
(
y
∣
X
θ
,
σ
2
I
)
N
(
θ
∣
m
0
,
S
0
)
d
θ
\begin{aligned} p(\mathcal Y|\mathcal X)&=\int p(\mathcal Y|\mathcal X, \theta)p(\theta)d\theta\\&=\int \mathcal N(y|X\theta,\sigma^2I)\mathcal N(\theta|m_0,S_0)d\theta\end{aligned}
p(Y∣X)=∫p(Y∣X,θ)p(θ)dθ=∫N(y∣Xθ,σ2I)N(θ∣m0,S0)dθ
上面这个式子可以理解为参数先验下的似然的期望:
E
θ
[
p
(
Y
∣
X
,
θ
)
]
\mathbb E_\theta[p(\mathcal Y|\mathcal X,\theta)]
Eθ[p(Y∣X,θ)]
计算边际似然需要两个步骤,首先先确定边际似然是高斯分布,然后计算出这个高斯分布的均值和方差。
由高斯分布的性质,两个高斯分布的乘积仍旧是高斯分布。
下面开始计算这个高斯分布的均值和方差:
E
[
Y
∣
X
]
=
E
θ
,
ϵ
[
X
θ
+
ϵ
]
=
X
E
θ
[
θ
]
=
X
m
0
,
ϵ
∼
N
(
0
,
σ
2
I
)
\mathbb E[\mathcal Y|\mathcal X]=\mathbb E_{\theta,\epsilon}[X\theta+\epsilon]=X\mathbb E_\theta[\theta]=Xm_0,\quad \epsilon \sim \mathcal N(0,\sigma^2I)
E[Y∣X]=Eθ,ϵ[Xθ+ϵ]=XEθ[θ]=Xm0,ϵ∼N(0,σ2I)
方差为:
Cov
[
Y
∣
X
]
=
Cov
θ
,
ϵ
[
X
θ
+
ϵ
]
=
Cov
[
X
θ
]
+
σ
2
I
=
X
Cov
θ
[
θ
]
X
⊤
+
σ
2
I
=
X
S
0
X
⊤
+
σ
2
I
\begin{aligned}\operatorname{Cov}[\mathcal Y|\mathcal X]&=\operatorname{Cov}_{\theta,\epsilon}[X\theta+\epsilon]=\operatorname{Cov}[X\theta]+\sigma^2I\\ &=X\operatorname{Cov}_\theta[\theta]X^\top+\sigma^2I=XS_0X^\top+\sigma^2I\end{aligned}
Cov[Y∣X]=Covθ,ϵ[Xθ+ϵ]=Cov[Xθ]+σ2I=XCovθ[θ]X⊤+σ2I=XS0X⊤+σ2I
所以,边际似然为:
p
(
Y
∣
X
)
=
(
2
π
)
−
N
2
det
(
X
S
0
X
⊤
+
σ
2
I
)
−
1
2
⋅
exp
(
−
1
2
(
y
−
X
m
0
)
⊤
(
X
S
0
X
⊤
+
σ
2
I
)
−
1
(
y
−
X
m
0
)
)
=
N
(
y
∣
X
m
0
,
X
S
0
X
⊤
+
σ
2
I
)
\begin{aligned} p(\mathcal{Y} \mid \mathcal{X})=&(2 \pi)^{-\frac{N}{2}} \operatorname{det}\left(\boldsymbol{X} \boldsymbol{S}_{0} \boldsymbol{X}^{\top}+\sigma^{2} \boldsymbol{I}\right)^{-\frac{1}{2}} \\ & \cdot \exp \left(-\frac{1}{2}\left(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{m}_{0}\right)^{\top}\left(\boldsymbol{X} \boldsymbol{S}_{0} \boldsymbol{X}^{\top}+\sigma^{2} \boldsymbol{I}\right)^{-1}\left(\boldsymbol{y}-\boldsymbol{X} \boldsymbol{m}_{0}\right)\right) \\&=\mathcal N(y|Xm_0,XS_0X^\top+\sigma^2I) \end{aligned}
p(Y∣X)=(2π)−2Ndet(XS0X⊤+σ2I)−21⋅exp(−21(y−Xm0)⊤(XS0X⊤+σ2I)−1(y−Xm0))=N(y∣Xm0,XS0X⊤+σ2I)
与之前的内容进行联系,为什么形式是这样的?
用正交投影解释极大似然估计(Maximum Likelihood as Orthogonal Projection)
考虑一个简单的线性规划模型:
y
=
x
θ
+
ϵ
,
ϵ
∼
N
(
0
,
σ
2
)
y=x\theta+\epsilon,\quad \epsilon \sim \mathcal N(0,\sigma^2)
y=xθ+ϵ,ϵ∼N(0,σ2)
由原先的提到的极大似然估计,得到斜率参数:
θ
M
L
=
(
X
⊤
X
)
−
1
X
⊤
y
=
X
⊤
y
X
⊤
X
∈
R
\theta_{ML}=(X^\top X)^{-1}X^\top y=\frac{X^\top y}{X^\top X}\in \mathbb R
θML=(X⊤X)−1X⊤y=X⊤XX⊤y∈R
其中,
X
∈
R
N
X\in \mathbb R^N
X∈RN和
y
∈
R
N
y\in \mathbb R^N
y∈RN为训练集中的元素(都是向量,所以
X
⊤
X
X^\top X
X⊤X为标量,这也是将这一项放到分母的原因)。
所以对应的目标为:
X
θ
M
L
=
X
X
⊤
y
X
⊤
X
=
X
X
⊤
X
⊤
X
y
X\theta_{ML}=X\frac{X^\top y}{X^\top X}=\frac{XX^\top}{X^\top X}y
XθML=XX⊤XX⊤y=X⊤XXX⊤y
所以可以理解为,我们的目标是找到
y
=
X
θ
y=X\theta
y=Xθ的解。由原先的线性代数和解析几何,可以将上式理解为y在X张成的一维子空间的正交投影,其中
X
X
⊤
X
⊤
X
\frac{XX^\top}{X^\top X}
X⊤XXX⊤为投影矩阵,
θ
M
L
\theta_{ML}
θML为y在一维子空间中的正交投影的坐标,
X
θ
M
L
X\theta_{ML}
XθML为
y
y
y在这个子空间中的正交投影。
所以,极大似然估计的解得到的是在
X
X
X子空间中找到一个与观测值
y
y
y最接近的向量。这里的距离表示
y
n
y_n
yn和
x
n
θ
x_n\theta
xnθ的最短(平方)距离

在广义的线性规划中:
y
=
ϕ
⊤
(
x
)
θ
+
ϵ
,
ϵ
∼
N
(
0
,
σ
2
)
y=\phi^\top(x)\theta+\epsilon,\quad \epsilon \sim \mathcal N(0,\sigma^2)
y=ϕ⊤(x)θ+ϵ,ϵ∼N(0,σ2)
其中,
ϕ
(
x
)
∈
R
K
\phi(x)\in \mathbb R^K
ϕ(x)∈RK,利用极大似然估计得到参数结果:
y
≈
Φ
θ
M
L
θ
M
L
=
(
Φ
⊤
Φ
)
−
1
Φ
⊤
y
\boldsymbol y\approx \Phi\theta_{ML}\\\theta_{ML}=(\Phi^\top\Phi)^{-1}\Phi^\top \boldsymbol y
y≈ΦθMLθML=(Φ⊤Φ)−1Φ⊤y
上式实际上就是一个往特征矩阵
Φ
\Phi
Φ张成的K维子空间的投影。若将特征矩阵
Φ
\Phi
Φ构造成规范正交,这时候
Φ
\Phi
Φ就形成了一个规范正交基。因为
Φ
⊤
Φ
=
I
\Phi^\top\Phi=I
Φ⊤Φ=I所以,对应的投影为:
Φ
(
Φ
⊤
Φ
)
−
1
Φ
⊤
y
=
Φ
Φ
⊤
y
=
(
∑
k
=
1
K
ϕ
k
ϕ
k
⊤
)
y
\Phi(\Phi^\top\Phi)^{-1}\Phi^\top \boldsymbol y = \Phi\Phi^\top \boldsymbol y=\begin{pmatrix} \sum\limits^K_{k=1}\phi_k\phi_k^\top\end{pmatrix}\boldsymbol y
Φ(Φ⊤Φ)−1Φ⊤y=ΦΦ⊤y=(k=1∑Kϕkϕk⊤)y
所以极大似然的投影这时候就是y向基向量
ϕ
k
\phi_k
ϕk的投影的和。
这部分需要深入理解一下,为什么?
the coupling between different features has disappeared due to the orthogonality of the basis.
Further Reading:
1.In deffenrent cases we may choose deffenrent model functions which corresponding to the likelihood function
2.generalized linear models:there is a a smooth and invertible function σ ( ⋅ ) \sigma(\cdot) σ(⋅)(which could be nonlinear), so that y = σ ( f ( x ) ) y = \sigma(f(x)) y=σ(f(x)),where f ( x ) = θ ⊤ ϕ ( x ) f(x)=\theta^\top \phi(x) f(x)=θ⊤ϕ(x) which also f ( x ) = σ ∘ f f(x)=\sigma\circ f f(x)=σ∘f. The first one is activate function, and the later one is linear function model. This can form a neural network model.
y = σ ( A x + b ) y=\sigma(Ax+b) y=σ(Ax+b),where A is weight matrix, b is bias vector so:
x k + 1 = f k ( x k ) f k ( x k ) = σ k ( A k x k + b k ) \begin{aligned} x_{k+1}&=f_k(x_k)\\f_k(x_k)&=\sigma_k(A_kx_k+b_k)\end{aligned} xk+1fk(xk)=fk(xk)=σk(Akxk+bk)
This is a K-layer deep neural network( f K − 1 ∘ ⋯ ∘ f 0 f_{K-1}\circ\cdots\circ f_0 fK−1∘⋯∘f0)




























 498
498











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








