机器学习中的数学：（二）解析几何

解析几何(Analytic Geometry)

这章将从几何的角度理解之前提及的一些概念。

范数(Norm)

范数实际上就是向量的一个长度

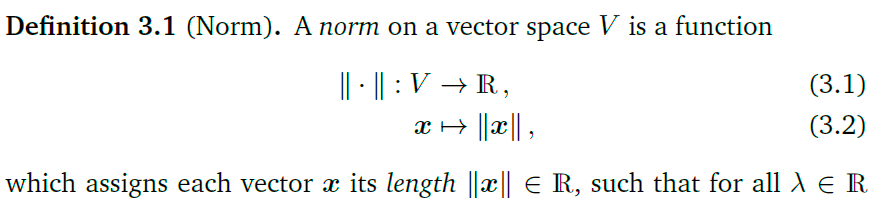
范数有以下性质：

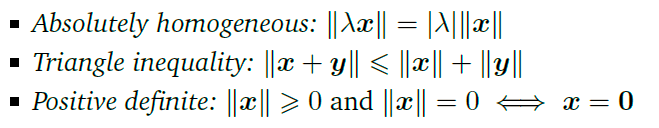
• 第一个绝对齐次（？）实际上数量积不就是对向量长度的一个延伸，所以，缩放的量可以提出来。
• 第二个三角不等式，因为两个向量和这两个向量的向量和会形成一个三角形，三角形有一个性质就是两边之和大于等于第三边
• 最后一个是因为长度是非负的

下面是两种不同的范数，这种区别是对距离的定于不同导致的。

曼哈顿范数（Manhattan Norm）

由上图可以了解到曼哈顿距离和欧几里得距离的区别，这样曼哈顿距离就是对应的向量（坐标）所有元素的绝对值之和。其实就是点在水平和竖直方向的位移总和。($x_i$表示向量的元素，$|\cdot |$表示绝对值)

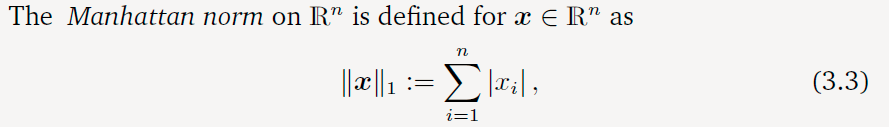
表示方式：${\ell }_1$

欧几里得范数（Euclidean Norm）

这个使用的就是直观的“直线距离”：

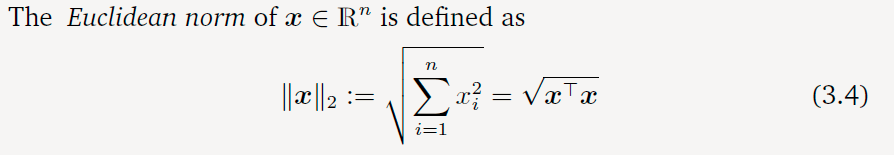
表示方式：${\ell }_2$

曼哈顿范数（左）和欧几里得范数（右）的实例：

内积（Inner Product）

内积可以理解为，两个向量在同一向量空间（转换后）下的长度的乘积。
点积：两维度相同的向量相乘最后得到一个实数。
$$x^{\top }y=\sum _{i=1}^n{x}_i{y}_i$$
点积的几何含义：

所以从图像上看，可以得到部分点积的性质：当两向量相反的时候，点积为负数；当两向量垂直的时候，点积为0（在另一个向量的投影的长度为0）。当两向量方向相同的时候，点积为正。
内积的齐次性和对称性：两个向量哪个投影至哪个其实并没有什么区别，所以，二者乘积的顺序是无关紧要的。

点积为什么是这样计算的？

广义内积

双线性映射（bilinear mapping）

当映射的参数顺序交换后，映射结果保持一致，这种性质称为对称(symmetric).当映射结果不会小于0， 这种性质称为正定（positive definite）

这样，内积的广义定义就是一个正定、对称的双线性映射。

内积空间是不是就是向量空间中两两通过运算之后得到一个实数的向量组成的空间？理解一下上图最后一句化的含义。

对称正定矩阵（Symmetric, Positive Definite Matrices）

由于内积是正定的，所以有上式可以得出：
∀ x ∈ V \ { 0 } : x T A x > 0 \forall x \in V \backslash \{0\}:x^T\bold Ax > 0 ∀x∈V\{0}:xTAx>0
$x$是任意的非零向量。
对于一个满足上式的对称矩阵，称为正定矩阵
∀ x ∈ V \ { 0 } : x T A x ≥ 0 \forall x \in V \backslash \{0\}:x^T\bold Ax \ge 0 ∀x∈V\{0}:xTAx≥0
满足上式的对称矩阵称为半正定矩阵

可以使用一个正定矩阵定义一个内积：


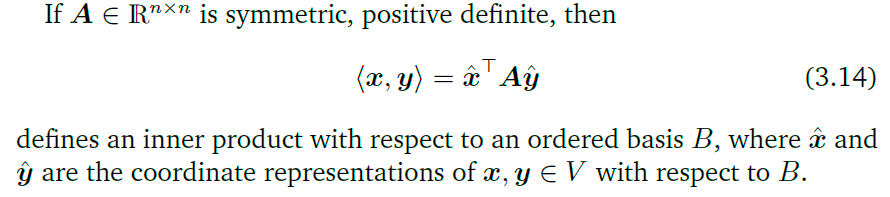
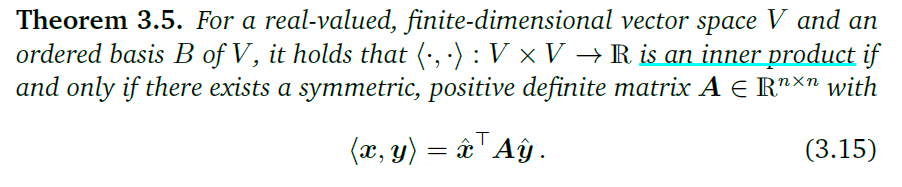
因为矩阵$\mathbf{A}$正定，所以${\mathbf{x}}^T\mathbf{A}\mathbf{x}>0$。这一就是说，$\mathbf{A}\mathbf{x}\ne 0$所以A的零空间只能是$0$。同时，对角线的元素都大于0，原因如下：

长度与距离（Lengths and Distances）

内积和范数之间的关系十分紧密。这样理解，（在欧氏几何内）内积其实就是一个向量在另一个向量上投影之后，得到的向量，这两个向量的长度的乘积就是内积。范数简单来说就是向量的长度。所以，两个相同的向量的内积就是这个向量的范数的平方。
$$\Vert x\Vert :=\sqrt{⟨x,x⟩}$$

柯西-施瓦茨不等式（Cauchy-Schwarz Inequality）：

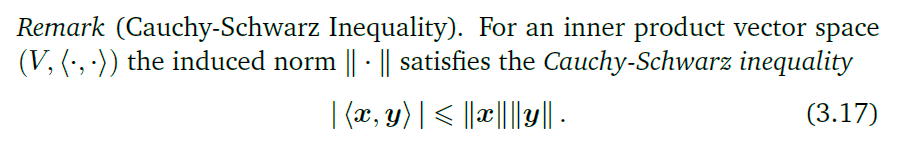
对于这个公式用图形非常好理解：不等式左边是投影之后的两向量的乘积（见之前点积部分介绍的投影），而右边是两向量没有经过投影的长度乘积。而只有两向量相等的时候，一个向量投影到另一个向量不会损失长度，这时候不等式取得等号，否则投影之后的向量长度都会变小。
在欧几里得空间中有特例：

距离和度规（Distance and Metric）：
距离的定义：

度规的定义：
在数学中，度量（度规）或距离函数是个函数，定义了集合内每一对元素之间的距离。

度规和内积有类似的性质，但是他们在某方面又是不同的。当两个向量越接近的时候，内积越大，而度规越小。

夹角与正交性(Angles and Orthogonality)

内积可以用于定义两向量的夹角：
由之前提到的的柯西-施瓦茨不等式：$$|⟨\mathbf{x},\mathbf{y}⟩|⩽\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert$$可以得到：
$$-1⩽\frac{⟨\mathbf{x},\mathbf{y}⟩}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }⩽1$$

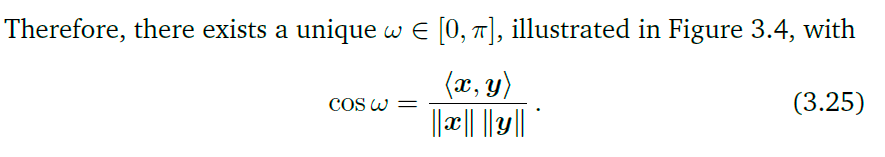
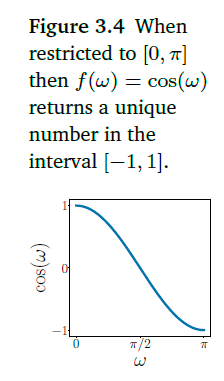在这个范围内，余弦函数的单调的。$\omega$用来表示两个向量的相近程度。
内积更重要的是可以为定义两向量的正交性:

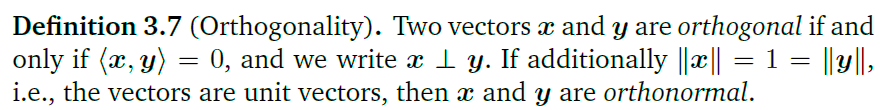
两向量正交实际上就是他们之间的夹角为$90°$,这时候的余弦值为0，由
$$\cos \omega =\frac{⟨\mathbf{x},\mathbf{y}⟩}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }$$
因为$\Vert \mathbf{x}\Vert$和$\Vert \mathbf{y}\Vert$都是正定的，所以当$\cos \omega =0$是，$⟨\mathbf{x},\mathbf{y}⟩$等于0.当x、y的范数（长度）为1时，称为规范化正交(orthonormal).当一个向量是$0$时，它与所有的向量都正交。
正交依赖于内积，所以在不同的内积的情况下，正交性可能不同。

正交矩阵

转置矩阵的变换关系？

$$\Vert Ax{\Vert }^{\top }=(Ax{)}^{\top }(Ax)=x^{\top }{A}^{\top }Ax=x^{\top }\mathbf{I}x=x^{\top }x=\Vert x{\Vert }^2$$
$$\cos \omega =\frac{(\mathbf{A}\mathbf{x}{)}^{\top }(\mathbf{A}\mathbf{y})}{\Vert \mathbf{A}\mathbf{x}\Vert \Vert \mathbf{A}\mathbf{y}\Vert }=\frac{{\mathbf{x}}^{\top }{\mathbf{A}}^{\top }\mathbf{A}\mathbf{y}}{\sqrt{{\mathbf{x}}^{\top }{\mathbf{A}}^{\top }\mathbf{A}\mathbf{x}{\mathbf{y}}^{\top }{\mathbf{A}}^{\top }\mathbf{A}\mathbf{y}}}=\frac{{\mathbf{x}}^{\top }\mathbf{y}}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }$$
由上可知，向量在经过正交变换之后，他们之间的夹角和长度都没有发生变化，实际上，正交变换就是将向量进行旋转操作。

规范正交基（Orthonormal Basis）

一对规范正交基满足两个条件，二者之间的夹角和他们各自的长度。 规范（长度为1）且正交（两对基相互垂直）

格拉姆-施密特正交化 Gram–Schmidt process
这里时利用高斯消元法来取得正交规范正交基

正交补（Orthogonal Complement）

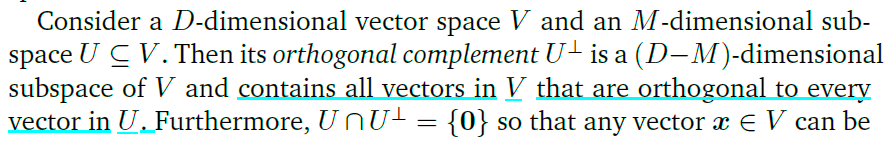
一个向量空间的两个子空间，这两个子空间的维度之和等于原先的向量空间的维度，准确来说，一个子空间占领原空间的部分维度，另一个子空间占领剩余的维度，二者在维度上没有关系。

一个实例

这样，原先向量空间中的任意向量，都可以用这个子空间的有序基以及其正交补的有序基表示出来（分解）：

$$\mathbf{x}=\sum _{m=1}^M{\lambda }_m{\mathbf{b}}_m+\sum _{j=1}^{D-M}{\psi }_j{\mathbf{b}}_j^{\perp },{\lambda }_m,{\psi }_j\in \mathbb{R}$$
其中，$\mathbf{x}$是原先的向量空间的一个向量，$\mathbf{b}$是原先空间的一个子空间的有序基，${\mathbf{b}}^{\perp }$是这个子空间的正交补的有序基。

函数的内积

有之前的点积：
$$x^{T}y=\sum _{i=1}^n{x}_i{y}_i$$
当向量的维度有无限维时，可以将这个利用定积分的定义，写成积分形式。
∫ a b f ( x ) = lim ⁡ λ → 0 ∑ i = 1 n f ( ξ i ) Δ x i , λ = m a x { Δ x 1 , Δ x 2 , . . . , Δ x n } \int_{a}^{b}f(x) = \lim_{\lambda \rarr 0}\sum_{i=1}^nf(\xi_i)\Delta x_i,\quad \lambda = max\{\Delta x_1,\Delta x_2,...,\Delta x_n\} ∫ab​f(x)=λ→0lim​i=1∑n​f(ξi​)Δxi​,λ=max{Δx1​,Δx2​,...,Δxn​}
从而：

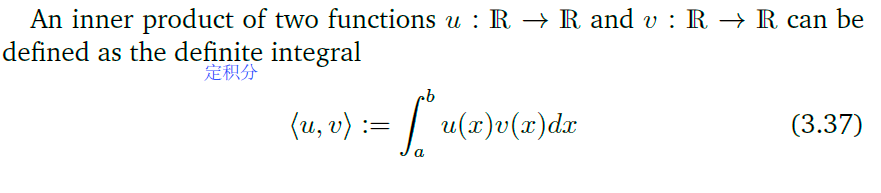
当两个函数在一定区间上的定积分为0时，说这两个函数时正交函数。

所有的正交函数够成的一个子空间
想要正确理解这个无穷维向量的内积，需要将积分延伸到希尔伯特空间（Hilbert space）中。

正交投影（Orthogonal Projections）

在机器学习中，由于研究对象通常由多标签组成的，所以就不得不使用高维矩阵，但是实际上，大多数的信息仅仅存储在少部分的标签中，所以，当需要对矩阵进行可视化或者数据压缩的时候，为了减少造成的信息损失，可以使用正交投影，这样压缩之后的数据损失最小。
下面是对投影的定义：

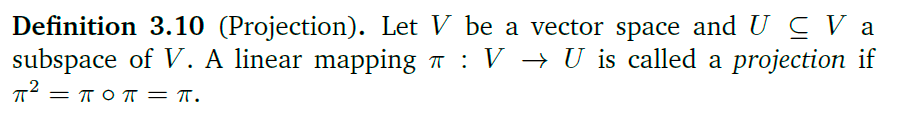
${\pi }^2=\pi \circ \pi =\pi$怎么理解？
应该是对一个向量进行两次投影的与进行一次投影的效果是一致的。 假设一个向量被正交投影到向量空间V中，然后再被正交投影到W中，那么这个向量可以直接利用一次正交变换投影到W中.
类似于$A\perp B,B\perp C\Rightarrow A\perp C$

投影本质上就是一种对向量的变换，所以可以用矩阵来描述，所以投影操作对应的矩阵就是投影矩阵（projection matrices，${\mathbf{P}}_{\pi }^2={\mathbf{P}}_{\pi }$）

正交投影到一维子空间

可以通过以下三步求解投影矩阵：

1.找到坐标$\lambda$:
$$⟨\mathbf{x}-{\pi }_U(\mathbf{x}),\mathbf{b}⟩=0\stackrel{{\pi }_U(\mathbf{x})=\lambda \mathbf{b}}{⟺}⟨\mathbf{x}-\lambda \mathbf{b},\mathbf{b}⟩=0$$注意到$\mathbf{x}-{\pi }_U(\mathbf{x})$是向量及其投影向量做差之后得到的向量，所以与投影到的向量正交。因为投影之后的向量属于向量空间U，所以可以用U中的有序基线性$\mathbf{b}$表示。
$$⟨\mathbf{x},\mathbf{b}⟩-\lambda ⟨\mathbf{b},\mathbf{b}⟩=0⟺\lambda =\frac{⟨\mathbf{x},\mathbf{b}⟩}{⟨\mathbf{b},\mathbf{b}⟩}=\frac{⟨\mathbf{b},\mathbf{x}⟩}{\Vert \mathbf{b}{\Vert }^2}.$$
这里是利用了内积的双线性的性质，将原先的式子进行了拆分，最后的等式是利用了内积的对称性。之后分离出$\lambda$，任务完成。
$$\lambda =\frac{{\mathbf{b}}^{\top }\mathbf{x}}{{\mathbf{b}}^{\top }\mathbf{b}}=\frac{{\mathbf{b}}^{\top }\mathbf{x}}{\Vert \mathbf{b}{\Vert }^2}$$
（这里探究当内积为点积的情况）

2.找到投影点（投影后的向量）：
$${\pi }_U(\mathbf{x})=\lambda \mathbf{b}=\frac{⟨\mathbf{x},\mathbf{b}⟩}{\Vert \mathbf{b}{\Vert }^2}\mathbf{b}=\frac{{\mathbf{b}}^{\top }\mathbf{x}}{\Vert \mathbf{b}{\Vert }^2}\mathbf{b}$$
将之前的结果带入式中，最后的等式为当内积为点积的时候成立。
$$\Vert {\pi }_U(\mathbf{x})\Vert \stackrel{(3.42)}{=}\frac{\left|{\mathbf{b}}^{\top }\mathbf{x}\right|}{\Vert \mathbf{b}{\Vert }^2}\Vert \mathbf{b}\Vert \stackrel{(3.25)}{=}|\cos \omega |\Vert \mathbf{x}\Vert \Vert \mathbf{b}\Vert \frac{\Vert \mathbf{b}\Vert }{\Vert \mathbf{b}{\Vert }^2}=|\cos \omega |\Vert \mathbf{x}\Vert .$$
点积为内积的情况下,同时，联立了$\cos \omega =\frac{⟨\mathbf{x},\mathbf{y}⟩}{\Vert \mathbf{x}\Vert \Vert \mathbf{y}\Vert }$

3.找到投影矩阵
$${\pi }_U(\mathbf{x})=\lambda \mathbf{b}=\mathbf{b}\lambda =\mathbf{b}\frac{{\mathbf{b}}^{\top }\mathbf{x}}{\Vert \mathbf{b}{\Vert }^2}=\frac{\mathbf{b}{\mathbf{b}}^{\top }}{\Vert \mathbf{b}{\Vert }^2}\mathbf{x}$$
于是：

$${\mathbf{P}}_{\pi }=\frac{\mathbf{b}{\mathbf{b}}^T}{\Vert \mathbf{b}{\Vert }^2}$$
这样看投影矩阵就是一个对称矩阵。

正交投影到一般的子空间

假设一个子空间$U\subseteq {\mathbb{R}}^n,dim(U)\ge 1$,因为投影的向量属于U，所以，这个投影向量可以用U的有序基表示出来：
$${\pi }_U(\mathbf{x})=\sum _{i=1}^m{\lambda }_i{\mathbf{b}}_i$$
1.找出投影的坐标${\lambda }_1,{\lambda }_2...,{\lambda }_n$:

$$\begin{gathered} {\pi }_U(\mathbf{x})=\sum _{i=1}^m{\lambda }_i{\mathbf{b}}_i=\mathbf{B}\lambda \\ \mathbf{B}=[{\mathbf{b}}_1,...,{\mathbf{b}}_m]\in {\mathbb{R}}^{n\times m},\lambda =[{\lambda }_1,...,{\lambda }_m{]}^T\in {\mathbb{R}}^m \end{gathered}$$
假设内积为点乘：
$$\begin{gathered} ⟨{\mathbf{b}}_1,\mathbf{x}-{\pi }_U(\mathbf{x})⟩={\mathbf{b}}_1^{\top }\left(\mathbf{x}-{\pi }_U(\mathbf{x})\right)=0 \\ ⋮ \\ ⟨{\mathbf{b}}_m,\mathbf{x}-{\pi }_U(\mathbf{x})⟩={\mathbf{b}}_m^{\top }\left(\mathbf{x}-{\pi }_U(\mathbf{x})\right)=0 \end{gathered}$$

由${\pi }_U=\mathbf{B}\lambda$,带入到上式中：
$$\begin{gathered} {\mathbf{b}}_1^T(\mathbf{x}-\mathbf{B}\lambda )=0 \\ ⋮ \\ {\mathbf{b}}_m^T(\mathbf{x}-\mathbf{B}\lambda )=0 \end{gathered}$$
转换成矩阵形式：
$$\begin{array}{rlr}\left[\begin{array}{c}{b}_1^{\top }\\ ⋮\\ b_m^{\top }\end{array}\right][x-B\lambda ]=0& ⟺B^{\top }(x-B\lambda )=0& ⟺B^{\top }B\lambda =B^{\top }x.\end{array}$$
因为$\mathbf{B}$是U的有序基，所以他是可逆的，所以可以得到：
$$\lambda =({\mathbf{B}}^T\mathbf{B}{)}^{-1}{\mathbf{B}}^T\mathbf{x}$$
其中：$({\mathbf{B}}^T\mathbf{B}{)}^{-1}{\mathbf{B}}^T$称为伪逆，可以用于计算非方阵矩阵。
2.找到投影向量：
由${\pi }_U=\mathbf{B}\lambda$,带入上式：
$${\pi }_U(x)=\mathbf{B}({\mathbf{B}}^T\mathbf{B}{)}^{-1}{\mathbf{B}}^T\mathbf{x}$$
3.找到投影矩阵：
由${\mathbf{P}}_{\pi }\mathbf{x}={\pi }_U(\mathbf{x})$,由上式可以得出：
$${\mathbf{P}}_{\pi }=\mathbf{B}({\mathbf{B}}^T\mathbf{B}{)}^{-1}{\mathbf{B}}^T$$

原始向量与投影向量之差够成的向量的范数，称为重构误差（reconstruction error.）或者投影误差。

虽然说${\pi }_U(\mathbf{x})\in {\mathbb{R}}^n$但是我们只需要用U的有序基就可以表示${\pi }_U(\mathbf{x})$

用正交投影可以用于求非齐次方程$\mathbf{A}\mathbf{x}=\mathbf{b}$无解的时候的近似解。当这个方程无解的时候，说明$\mathbf{x}$和$\mathbf{b}$不在同一个向量空间中，所以无法通过一些变换（$\mathbf{A}$）得到$\mathbf{b}$。这时候可以利用正交投影，将其中一个向量投影到另一个向量的向量空间中，这样可以得到一个近似解，其中的主要思想就是找到一个在A的张成空间中，与b最相近的向量。这样得到的解称为最小二乘解（least-squares solution）

格拉姆-施密特正交化（Gram-Schmidt Orthogonalization）

这里的目标是求出$u_2$，利用已知的数据$b_2,u_1$计算出${\pi }_{span[u_1]}(b_2)$这样就可以利用$b_2,{\pi }_{span[u_1]}(b_2)$计算$u_2$了。

我们可以使用向量以及其投影所在的向量空间的有序基作差，得到一个法向量。然后递归地将有序基转化成正交基。
$$\begin{gathered} u:={\mathbf{b}}_1 \\ {u}_k:={\mathbf{b}}_k-{\pi }_{span[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_{k-1}]}({\mathbf{b}}_k),k=2,\dots ,n \end{gathered}$$
其中，${\mathbf{b}}_k$是之前缔造的正交向量组成的向量空间（${\mathbf{u}}_1,\dots ,{\mathbf{u}}_{k-1}$）

在仿射空间中的正交投影

先将目标向量与支撑点(${\mathbf{x}}_0$)相减，得到的向量就是以仿射空间为起点的，这时候，问题就转换成我们之前讨论过的问题了。$${\pi }_L(\mathbf{x})={\mathbf{x}}_0+{\pi }_U(\mathbf{x}-{\mathbf{x}}_0)$$

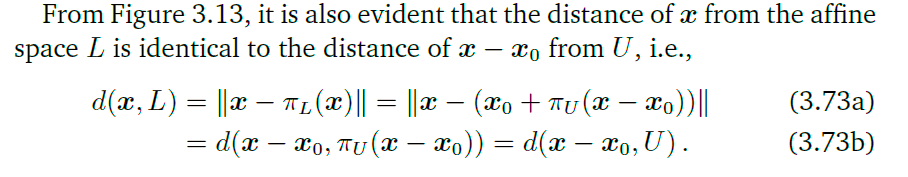
旋转变换

旋转实际上就是一种正交变换。在文中规定当旋转角度为正数的时候，图像作逆时针旋转。

在二维实空间中的旋转（Rotations in ${\mathbb{R}}^2$）

因为旋转之后的基向量仍然是线性无关的，所以，旋转也是一种基变换。由上可以得到旋转矩阵（旋转之后的向量）：
$$\Phi \left({\mathbf{e}}_1\right)=\left[\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right],\Phi \left({\mathbf{e}}_2\right)=\left[\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right]$$
$$\mathbf{R}(\theta )=\left[\begin{array}{ll}\Phi \left({\mathbf{e}}_1\right)& \Phi \left({\mathbf{e}}_2\right)\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right].$$

在三维实空间中的旋转(Rotations in ${\mathbb{R}}^2$)

可以这样理解，先固定一个坐标轴，然后从上往下看去，得到这个向量在另外两个基向量所形成的向量空间中正交投影，然后再作相应的旋转操作。

关于${\mathbf{e}}_1$的旋转操作：
$${\mathbf{R}}_1(\theta )=\left[\begin{array}{ccc}\Phi ({\mathbf{e}}_1)& \Phi ({\mathbf{e}}_2)& \Phi ({\mathbf{e}}_3)\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right]$$
类似的，只要固定哪个坐标轴，哪个坐标轴就是基向量。

在$n$维空间中的旋转

吉文斯旋转（Givens Rotation）：

实际上就是等价于单位矩阵对应位置上变成一个正弦或者余弦值。

旋转的特性

简单来说就是变换之后向量之间的距离角度不变，三维及三维以上的旋转操作不满足交换律，二维的满足。