傅里叶变换

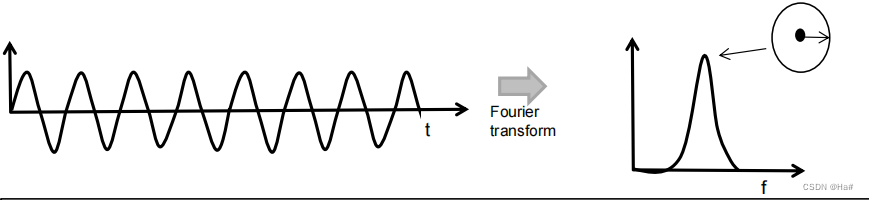
- 时域中的正弦波会在频域产生一个尖峰,该尖峰的位置与正弦波的频率相对应
- 频域中的信号是包含振幅和相位的复数,因此此处的图虽表示傅里叶变换的振幅,但此处的每个值实际上是一个包含振幅和相位的复数。
- 一个复数可以在数学上表示为Ae的jθ次方(A是振幅,θ是相位)

- 也可将其以图形方式表示为一个向量(该向量是一个矢量,具有与振幅A相对应的长度以及与相位θ相对应的方向)

- 傅里叶变换的重要性质是峰值的相位对应于正弦波的初始相位。所以说,这里的正弦波以特定的初始相位开始,在傅里叶变换中,该相位反映在此处峰值的相位中。如图,下方正弦波与上方正弦波的频率相同,但是起始相位与该相位相差90度,所以傅里叶变换也将具有一个峰值且位置与之相同,但相位与该前一个峰值相比偏移了90度。

中频信号的相位1

- 顶部的图显示了TX线性调频脉冲的A-t图,中间的图是RX线性调频脉冲,它是TX线性调频脉冲的延迟版本,延迟量为τ,τ是往返延迟。IF信号是一个具有恒定频率的信号即单个正弦波。
- 所以,从数学角度而言,我们可以将IF信号表示为Asin(2𝛑ft+𝛟0)。其中频率f由S2d/c给出,S是斜率,d是到物体的距离,c是光速,相位𝛟0正是IF信号在该点c的相位。
- 混频器输出中IF信号的初始相位是两个输入的初始相位的差值,所以c处的相位,还是与𝛟0相同,即A点处的TX线性调频脉冲相位与B点处的RX线性调频脉冲相位之间的差值。
中频信号的相位2
- 现在如果物体移动了一小段距离,从而使往返延迟τ更改为Δτ,IF信号的相位如何变化?
- 注意:这里的蓝色曲线表示新的RX信号将移动Δτ的距离,IF信号也将相应的发生变化。现在,新的IF信号的起始相位——即带点F处的IF信号相位,将为D处的相位与E处的相位之间的差值,现在,E处的RX线性调频脉冲的相位将与先前B处的相位相同。但D处的TX线性调频脉冲相位将与先前A处的相位,具有额外的相位偏移2𝛑fcΔτ,这是因为TX线性调频脉冲在该Δτ期间会移动额外的相位2𝛑fcΔτ。这个额外的相位,即A和D处的相位差,直接反映在IF信号的相位中——即F处的相位。

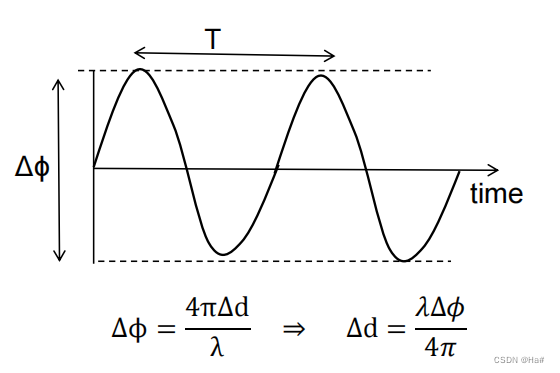
- 所以,当物体移动Δτ时IF信号的相位变化,由Δ𝛟等于2𝛑fcΔτ给出。我们还可以根据相应的到物体的距离变化Δd将其改写为4𝛑Δd除以𝜆(利用了Δτ等于距离变化的两倍除以光速,以及波长等于光速除以频率fc)
- IF信号总结:对于雷达前方的单个物体,IF信号是频率与物体的距离成正比的音调,它的起始相位具有随物体距离的微小变化Δd以线性方式变化的性质
中频信号对物体中小位移的灵敏度
- 对于距离雷达d的物体,中频信号将是一个正弦信号,其相位以线性方式响应到物体的距离微小变化Δd(该微小指的是与雷达的距离分辨率相比是微小的)

-
如果雷达前的物体改变其位置1mm,它是一个斜率为每毫秒50MHz且持续时间为40毫秒的线性调频脉冲,注意,对于77GHz雷达,我们的1毫米实际上对应于波长的1/4。
如果该物体的位置改变1毫米,IF信号的相位变化Δ𝜙 = 4𝜋Δ𝑑/𝜆 = 𝜋 = 180度
IF信号的频率变化Δf = S2Δ𝑑/𝑐 = 50x1012x2x1x10−3/(3x108) = 333Hz
在Tc等于40微秒的观测窗口中,Δ𝑓𝑇𝑐=333x40x10−6=0.013周期,这个变化在频谱中就无法识别。
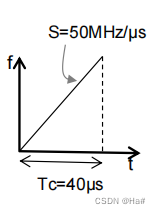
- 重点:IF信号的相位对物体距离的微小变化非常敏感,但是频率对此类微小的变化非常的不敏感
-
位于特定距离的物体会产生具有特定频率和相位的IF信号,下图是是与单个物体相对应的IF信号,它是一个具有特定频率和特定起始相位的正弦波,在该图中起始相位为0。傅里叶变换会生成单个峰值。该峰值的相位对应于此正弦波的起始相位。
现在将物体移动一小段距离,如下图,起始相位改变了,改变了180度,相应地,FFT的峰值的位置保持不变,但峰值的相位改变了180度。

两次线性调频脉冲测量物体的速度

-
思想:发射两个间隔时间为Tc的线性调频脉冲,与其中每个线性调频脉冲相对应的距离FFT将在相同的位置具有峰值,但是具有不同的相位。这两个峰值的相位之间的测量相位差w将与物体的运动直接对应。注意,如果物体的速度为v,则该物体在此时间段Tc内的移动距离将为v*Tc

峰值之间的相位差对应于,这两个发射线性调频脉冲的峰值相位之间的相位差由4𝜋乘以物体在该期间内移动的距离然后除以𝜆给出,注意,在两个连续的线性调频脉冲之间测量的相位差可用于估算物体的速度
对振动物体的测量
-
下图描述了以振荡方式移动的物体随时间演变的过程,这可以表示一个正在振荡的物体,假设运动距离非常的小,所以该物体的最大位移Δ𝑑是波长的一小部分。
如果我们在这个振荡物体前面放置一个雷达并发射一系列等间隔的线性调频脉冲,众所周知,每个TX线性调频脉冲会产生一个反射线性调频脉冲,并且经处理的IF信号会在距离FFT中产生一个峰值,Ad非常小,导致该峰值的频率不会在线性调频脉冲之间改变太多。但峰值的相位将会响应该物体的振荡移动

相位的时间演化可以用来估计振动的振幅和周期性
我们有多个物体,他们具有不同的相对于雷达的速度,测量时,这些物体到雷达的距离几乎相同,那么,距离FFT显然将向您显示仅有单个与该距离d对应的峰值,那么怎么分离这些物体呢?事实证明,相对于雷达具有相同距离但具有不同速度的物体,可以使用多普勒FFT的工具进行分离


























 1014
1014

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










