信息
instant-ngp是英伟达于2022年7月推出的一种快速训练方法,具有多分辨率哈希编码的即时神经图形原语,论文讲解视频:B站视频;设计了一个新的通用性的输入编码,它可以使用小型的网络同时又不会降低质量,小型的网络可以显著的减少浮点数的计算和内存访问,多分辨率的结构可以使网络自己处理哈希碰撞的问题,NGP使用了完全的cuda编程,更小的带宽浪费和更少的计算
1920x1080分辨率的图像可以在10ms完成渲染
Title:Instant Neural Graphics Primitives with a Multiresolution Hash Encoding
Paper:https://ar5iv.labs.arxiv.org/html/2201.05989
Code:https://nvlabs.github.io/instant-ngp
简介
文章设计了一种通用的输入编码方式降低全连接网络的时间成本,同时不牺牲质量的情况下可以使用小的网络结构来显著减少浮点数和内存访问操作的次数。核心点在于多分辨率的hash表,其中的值通过随机梯度下降优化并且通过神经网络就可以消除hash冲突;使用cuda编程速度更快。
为什么要对输入进行编码?
因为MLP拟合低频的特征更好,所以为了学得高频特征,不至于输出图像过于平滑,需要映射到更高维空间进行编码。
多分辨率hash表优点:
- 适用性好:将一系列网格映射到相应固定大小的特征向量阵列。粗分辨率:网格点到特征向量:1:1映射;细分辨率:阵列被视作hash表,用hash函数索引。(这种hash冲突是的训练梯度平均,与loss最相关的最大梯度占主导地位,于是hash表自动对最重要的精细尺度的稀疏区域优先级排序,与之前工作不同的是,在训练期间任何时候都不用对数据结构进行结构的更新);
- 效率高:hash查找时间复杂度是O(1),很好映射到GPU,看并行查询所有分辨率的hash表。
相关工作
介绍了之前的神经网络编码方式。
-
机器学习的输入编码:one-hot;kernel技巧;
-
频率编码:
a. 位置编码(nerf)
b. one-blob编码 -
参数编码:参数编码是除了权重和偏置之外,增加一种辅助类型的数据结果,如网格或者树可以根据输入向量,在这些结构上(网格或者树),使用插值的方式获取值;
这种安排用更大的内存占用换取更小的计算成本:对于通过网络向后传播的每个梯度,完全连接的MLP网络中的每个权重都必须更新,对于可训练的输入编码参数(“特征向量”),只有非常小的数量受到影响;(牺牲内存换精度)
例如,网格类型中的一个点位的值,其计算使用三线性插值的方式,只需要计算周围八个点的数据,通过这种方式,尽管参数编码的参数总数比固定的输入编码要高得多,但在训练期间进行更新所需的FLOPs和内存访问的数量并没有显著增加,通过减少MLP的大小,训练速度可以得到提升,并且不会降低质量; -
稀疏参数编码:
密集网络有两种浪费:
a.在空间中的空白部分,也会进行分配,也会进行特征计算,但是它们是无用的:参数的数量是N的三次方,但是有用的物体表面的数据是N的2次方,这个N可以认为是分辨率;
b.密集型网格会容易学习的过度平滑;
hash冲突:
没有通过探测、桶化或链接等典型方式明确处理哈希函数的冲突。而是依靠神经网络来学习消除哈希冲突本身的歧义,避免控制流分歧,降低实现复杂性并提高性能。另一个性能优势是哈希表的可预测内存布局,它独立于所表示的数据。
方法
多分辨率哈希编码
多分辨率哈希编码是论文核心部分,讲的就是如何对输入
x
x
x进行编码
y
=
e
n
c
(
x
;
θ
)
y=enc(x;\theta)
y=enc(x;θ)的过程,编码过程:
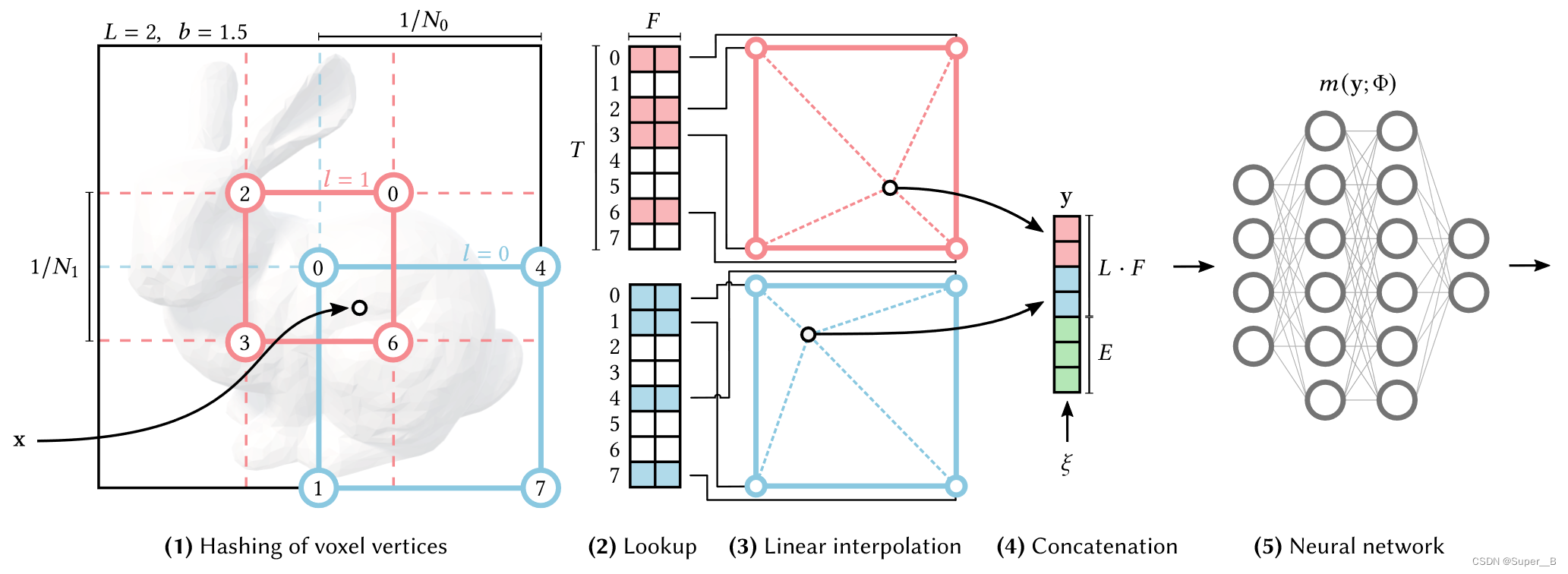 超参数含义:
超参数含义:
 图中各顶点代表特征向量,每个向量长度为
F
F
F,
N
l
N_{l}
Nl可以代表分辨率,最粗糙和最精细的取值范围:
[
N
m
i
n
,
N
m
a
x
]
[N_{min},N_{max}]
[Nmin,Nmax],每一级
l
l
l的值可以缩放为如下公式,
b
∈
[
1.26
,
2
]
b\in[1.26,2]
b∈[1.26,2]是生长因子,控制
N
l
N_{l}
Nl的值:
图中各顶点代表特征向量,每个向量长度为
F
F
F,
N
l
N_{l}
Nl可以代表分辨率,最粗糙和最精细的取值范围:
[
N
m
i
n
,
N
m
a
x
]
[N_{min},N_{max}]
[Nmin,Nmax],每一级
l
l
l的值可以缩放为如下公式,
b
∈
[
1.26
,
2
]
b\in[1.26,2]
b∈[1.26,2]是生长因子,控制
N
l
N_{l}
Nl的值:

- 按分辨率缩放:考虑单个分辨率 l l l时,输入的 x x x按分辨率缩放为: ⌊ x l ⌋ : = ⌊ x ⋅ N l ⌋ \lfloor{x_{l}}\rfloor:=\lfloor{x\cdot N_{l}}\rfloor ⌊xl⌋:=⌊x⋅Nl⌋, ⌈ x l ⌉ : = ⌈ x ⋅ N l ⌉ \lceil{x_{l}}\rceil:=\lceil{x}\cdot N_{l}\rceil ⌈xl⌉:=⌈x⋅Nl⌉。限制上下界,就可以固定在一个方格里面;
- hash:其中每个顶点可以映射到长度为
T
T
T的特征向量数组。对于粗网络顶点数<
T
T
T,则可以1:1映射;而对于精细网络需要用散列函数索引到数组(如下所示),且不需要显示处理hash冲突;

- d-线性插值:根据 x x x的相对位置,对每个顶点特征向量进行线性插值,插值权重是 w l : = x l − ⌊ x l ⌋ w_{l}:=x_{l}-\lfloor{x_{l}\rfloor} wl:=xl−⌊xl⌋;
- 拼接:把每一级 l l l插值结果拼接起来并加入辅助输入 ξ ∈ R E \xi\in R^{E} ξ∈RE(如神经辐射中的视图方向和纹理)产生 y ∈ R L F + E y\in R^{LF+E} y∈RLF+E,这就是编码后的 e n c ( x ; θ ) enc(x;\theta) enc(x;θ)送入MLP m ( y ; Φ ) m(y;\Phi) m(y;Φ)的输入;
隐式哈希冲突解决方案
不同
x
x
x坐标散列到特征向量数字同一索引时,产生冲突,但这种碰撞是伪随机分布,不太可能在给定的一对点的每个级别同时发生。
为什么作者说不用显式处理冲突?
答:相撞的两点对样本重建的重要性很少完全相等。比如说nerf中可见表面的一点对重建的图像有更大贡献(有高可见度和高密度,就会成倍影响梯度大小),而空白的地方一点权重更小,最终就是重要的点梯度主导了冲突平均值,使得自然优化了这种冲突。
实验
超参数设置( F = 2 , L = 16 F=2,L=16 F=2,L=16), T T T越大质量越好,但是占用内存大性能就越低。用cuda编程提高性能。对四个类型任务测试:
- 百万像素图像:高分辨率图像的渲染
- SDF
- NRC
- NERF
只关注nerf部分:也就是把编码用到MLP的输入上。和原始nerf不同的是:
- 原始NeRF使用了两次MLP,一次粗模型训练,一次精细模型训练;
- NGP并无没有区分粗网络和精细网络,NGP的粗糙精细体现在了不同Level上;
- NGP使用了两个MLP,一个负责计算体积密度,第二个在其后面计算RGB;
第一个MLP只有一个隐藏层,第二个MLP有两个隐藏层,这比原始NeRF的MLP要少很多:
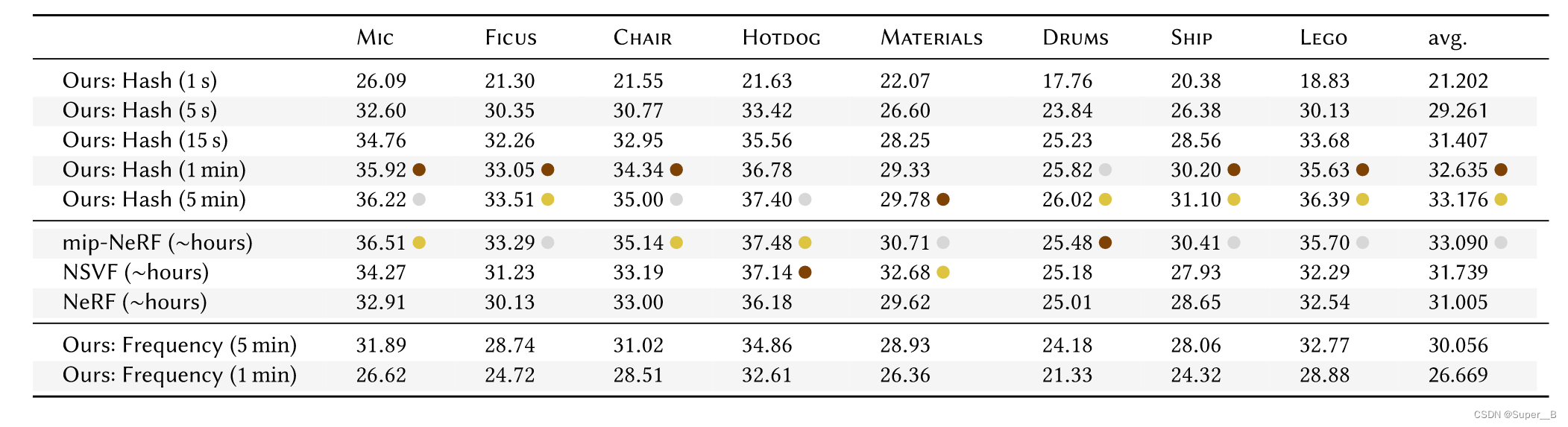







 instant-ngp是一种由英伟达推出的快速训练方法,采用多分辨率哈希编码,能以小规模网络实现高质量渲染,减少计算和内存需求。该技术利用CUDA编程提升效率,通过隐式处理哈希冲突,适用于高分辨率图像渲染和神经辐射场(NeRF)等任务。实验表明,这种方法在保持质量的同时提高了性能。
instant-ngp是一种由英伟达推出的快速训练方法,采用多分辨率哈希编码,能以小规模网络实现高质量渲染,减少计算和内存需求。该技术利用CUDA编程提升效率,通过隐式处理哈希冲突,适用于高分辨率图像渲染和神经辐射场(NeRF)等任务。实验表明,这种方法在保持质量的同时提高了性能。
















 5273
5273

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








