Physics-informed Neural Network for Nonlinear Dynamics in Fiber Optics论文笔记

最新推荐文章于 2025-03-11 16:51:40 发布
最新推荐文章于 2025-03-11 16:51:40 发布
阅读量1.3k 收藏 22
点赞数 11
分类专栏： 物理驱动深度学习论文分享 文章标签： python
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45521594/article/details/120167854
版权
该研究利用Physics-Informed Neural Networks (PINN)解决光纤中的非线性动力学问题，深入探讨了dispersion、self-phase modulation和高阶非线性效应。通过将峰值功率作为额外输入，PINN能适应不同场景，展示出良好的泛化能力和优于数据驱动神经网络的性能，同时需要较少的数据和较低的计算复杂度。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

Physics-informed Neural Network for Nonlinear Dynamics in Fiber Optics

  • 作者：
    Xiaotian Jiang1, Danshi Wang1,∗, Qirui Fan2, Min Zhang1, Chao Lu3, and Alan Pak Tao Lau2
  • 时间：2021
  • 期刊：arixiv

摘要

  • 研究PINN求解用于学习光纤非线性动力学的Schrödinger方程，对多种物理效应进行深入研究，包括dispersion, self-phase modulation, and higher-order nonlinear effects。special case (soliton propagation) and general case (multi-pulse propagation)也被研究。
  • 以前的PINN主要在单一情况下有效，为了克服这一问题，物理参数（子脉冲的峰值功率和振幅）作为附加的输入参数，使PINN能够学习不同场景的物理约束，具有良好的泛化性能
  • PINN表现出比数据驱动神经网络更好的性能同时使用更少的数据，其计算复杂度(从乘法数来看)远远低于分步傅里叶方法。

问题定义

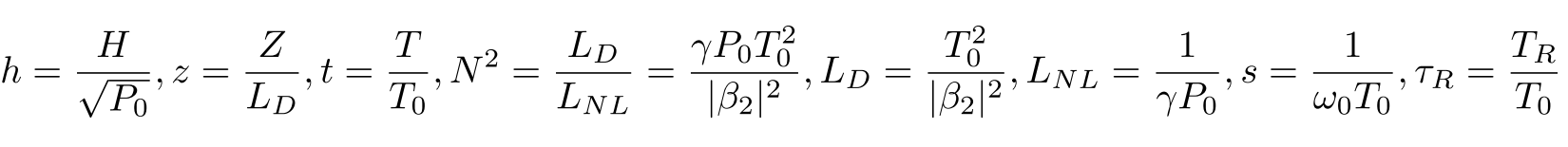
Nonlinear Dynamics in Fiber Optics问题可以描述为在这里插入图片描述
其中
在这里插入图片描述
通过分解实部与虚部，该问题可被定义为

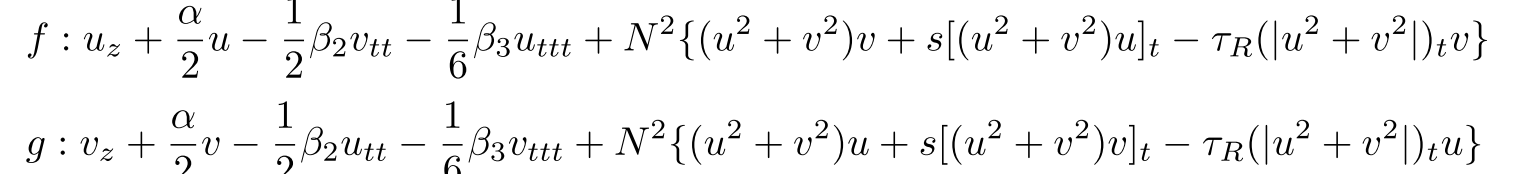
在这里插入图片描述
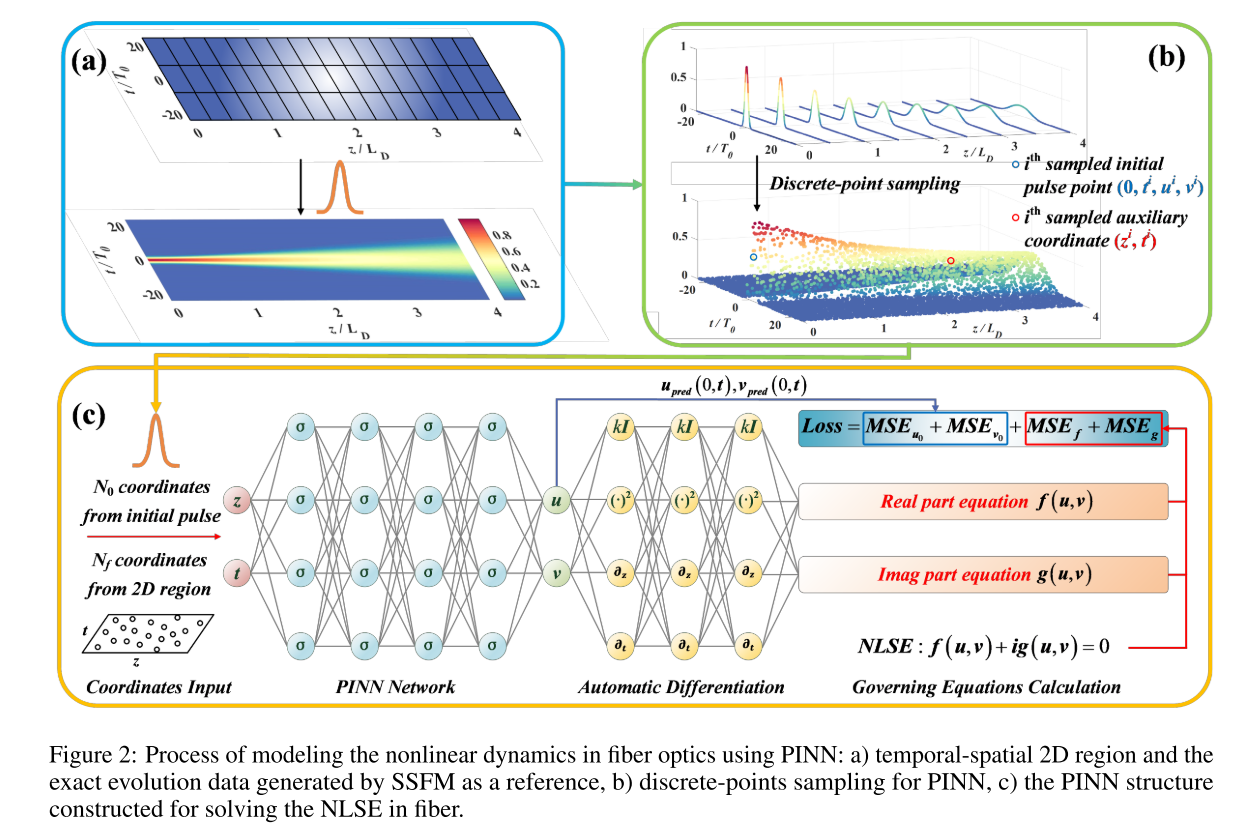
在这里插入图片描述

方法

  • 输入为(z,t)
    在这里插入图片描述

针对求解的问题，PINN损失函数定义为
在这里插入图片描述
上式前两项是初值构建的约束，后两项是满足PDE的约束。

  • 输入为(z,t,p)，其中p是峰值，(被拉成一列作为输入)
    在这里插入图片描述

实验结果

在这里插入图片描述

思考

  • 这里提到了不同峰值功率值作为输入，得到不同峰值功率下的求解域。
【论文全文翻译、剖析+代码复现】一种新基于PINN的机器学习算法来模拟辐射传输
源代码杀手的博客
01-22 879
这篇论文提出了一个新的方法，利用物理信息神经网络（PINN）来模拟辐射传输。辐射传输在许多领域中都有广泛应用，例如天文学、气候模型、辐射热传输等，但传统的数值方法（如有限差分、有限元法等）通常需要大量的计算资源，并且对于复杂的几何和物理条件的处理不够灵活。为了克服这些挑战，作者提出了基于PINN的算法。
物理信息神经网络PINNs : Physics Informed Neural Networks 详解
A book super
05-08 4万+
本博客主要分为两部分： 1、PINN模型论文解读 2、PINN模型相关总结 一、PINN模型论文解读 1、摘要： 基于物理信息的神经网络（Physics-informed Neural Network， 简称PINN），是一类用于解决有监督学习任务的神经网络，同时尊重由一般非线性偏微分方程描述的任何给定的物理规律。 原理：它不仅能够像传统神经网络一样学习到训练数据样本的分布规律，而且能够学习到数学方程描述的物理定律。 优势：与纯数据驱动的神经网络学习相比，PINN在训练过程中施加了物理信息约束，因而能用更少
基于物理信息的神经网络（Physics-informed Neural Networks；PINNs）Part-1（简单介绍）
早起CaiCai的学习空间
06-03 4931
基于物理信息的神经网络（Physics-informed Neural Networks；PINNs）Part-1（简单介绍）
学习笔记：物理信息神经网络(PINN)
qq_52635735的博客
03-11 2586
PINN 的强大在于它打破了传统数值方法的限制，将神经网络的非线性拟合能力与物理方程的严谨性结合起来。它在处理高维、数据稀缺、复杂物理约束的场景下尤其出色。当然，PINN 也有收敛慢、梯度消失等挑战，比如，复杂 PDE 可能导致梯度传播困难，收敛慢(梯度消失)、于具有快速变化特征的系统，如冲击波，标准 PINN 可能精度不足，需要改进策略，比如自适应采样或多尺度特征提取。但随着研究深入，这些问题正在不断被解决。物理或化学方程为什么往往是偏微分方程？什么是物理信息神经网络(PINN)?x_%7Bi%7D。
PINN(Physics-informed Neural Networks)之入门
qq_45776432的博客
02-25 3364
PINN(Physics-informed Neural Networks)之入门主要从high-level的角度先引入物理模拟主要是要做一件什么事，然后深入浅出地更进一步解释了PINN文章具体的情况。
PINN——加入物理约束的神经网络
qq_39444290的博客
12-17 2649
【摘要】 基于物理信息的神经网络(Physics-informed Neural Network， 简称PINN)，是一类用于解决有监督学习任务的神经网络，它不仅能够像传统神经网络一样学习到训练数据样本的分布规律，而且能够学习到数学方程描述的物理定律。与纯数据驱动的神经网络学习相比，PINN在训练过程中施加了物理信息约束，因而能用更少的数据样本学习到更具泛化能力的模型。本文主要解析这种神经网络以...
用于求解二维磁场的物理约束的神经网络（论文学习笔记）
qq_36823261的博客
08-12 2271
物理信息神经网络（PINN）在电气工程中的逆设计和参数设计问题上显示出巨大潜力。此外，关于 PINN 的现有著作大多致力于计算流体，很少有人关注电气工程应用中的多介质静态和低频电磁近场。本研究提出了一种用于求解电磁设备和系统中二维（2D）静态磁场的 PINN。磁场强度和磁矢量势通过训练神经网络求解，神经网络将偏微分方程和边界条件编码为残差。消除了对 PINN 训练产生负面影响的介质构成的参数空间导数的计算。为了进一步提高 PINN 的性能，还提出了一种网格辅助非均匀采样法来选择配点。
hPINN: 带硬约束的物理感知神经网络使用教程
gitblog_00705的博客
08-31 1286
hPINN: 带硬约束的物理感知神经网络使用教程 项目地址:https://gitcode.com/gh_mirrors/hp/hpinn 1. 项目介绍 hPINN（带有硬约束的物理感知神经网络）是一个开源项目，由Lu Lu等人开发，其成果发表在《SIAM Journal on Scientific Computing》上。这个项目专注于利用物理知识引导的神经网络解决流体动力学中的Stokes流...
ICCV2017论文摘要汇总
super_chicken的博客
04-18 6921
1. Globally-Optimal Inlier Set Maximisation for Simultaneous Camera Pose and Feature Correspondence Abstract: Estimating the 6-DoF pose of a camera from a single image relative to a pre-computed 3D p...
（三十二 ：2021.01.12）MICCAI 2017 追踪之论文纲要
Jojo论文基地
01-11 2792
讲在前面 PART I、PART II和PART III。 论文目录 PART I Atlas and Surface-Based Techniques（地图集和基于表面的技术） 概要 1.The Active Atlas: Combining 3D Anatomical Models with Texture Detectors有效地图集：将3D解剖模型与纹理探测器相结合 2.Exploring Gyral Patterns of Infant Cortical Folding Ba
个人网页、博客、课程--不断更新
qq_27009517的博客
12-18 2809
论文和相关代码 ：https://paperswithcode.com/ Caiming Xiong http://www.stat.ucla.edu/~caiming/ 论文，代码，博客 肖小粤的啵嗑 http://xiaoxiaoyue.me/ 博客记录 小土刀 https://wdxtub.com/ 博客记录 博客 http://ruder.io/multi-task/...
phygnn:物理学指导的神经网络（phygnn）
03-18
菌素 phygnn （fi-geon | ˈfi-jən）名词。 物理学指导的神经网络 一只稀有的神话鸟 物理学指导的神经网络的这种实现通过通用的损失项增强了传统的神经网络损失功能，该损失项可用于指导神经网络学习物理或理论约束。 phygnn使科学软件开发人员和数据科学家能够轻松地将机器学习模型集成到物理和工程应用程序中。当将纯数据驱动的机器学习模型应用于科学应用时，例如当机器学习模型产生物理上不一致的结果或难以推广到样本外场景时，此框架应有助于缓解一些经常遇到的挑战。 有关phygnn类框架的详细信息，请参见 例如，使用phygnn架构进行回归，分类甚至GAN应用，请参见 在国家可再生能源实验室（NREL），我们使用phygnn框架来补充传统的基于卫星的云属性预测模型。当传统的机械模型失效时，我们使用phygnn预测云的光学特性，并使用基于张量的完整辐射传递模型作为物理损耗函数，将预测
带硬约束的物理信息神经网络（PINN with Hard Constraint）示例及代码
m0_72768523的博客
04-19 3803
本文以一个案例介绍了带硬约束的物理信息神经网络的原理及实现步骤。
用物理信息神经网络（PINN）解决实际优化问题：全面解析与实践
最新发布
2501_90186640的博客
03-11 2125
本文系统介绍了物理信息神经网络（PINN）在解决实际优化问题中的创新应用。通过将物理定律与神经网络深度融合，PINN在摆的倒立控制、最短时间路径规划及航天器借力飞行轨道设计等复杂任务中展现出显著优势。实验表明，PINN相比传统数值方法及强化学习（RL）/遗传算法（GA），在收敛速度、解的稳定性及物理保真度上均实现突破性提升。
【小白记录深度学习】——物理信息神经网络（PINNs）
faderbitch的博客
07-22 9735
PINNs（Physics - informed Neural Networks，物理信息神经网络）的基本原理是应用神经网络来近似解决物理问题，将物理原理（用偏微分方程数学表达）作为先验知识，通过对偏微分方程残差的惩罚来实现。
Physics-informed neural networks for inverse problems in nano-optics and metamaterials
山里娃的博客
12-18 2295
论文信息 题目：hysics-informed neural networks for inverse problems in nano-optics and metamaterials 作者：Yuyao Chen, Lu Lu, George Em Karniadakis, and Luca Dal Negro 期刊会议：Computational Physics 年份：19 论文地址： 代码： 内容 动机 动机： 在强多光散射条件下，复杂多粒子几何中物理驱动的光散射微分模型的逆问题成为一个本质上不定的
物理约束相关问题梳理
allein_STR的博客
09-03 910
1. 问题及动机 尽管使用偏微分方程的数值离散化来模拟多物理问题取得了很大进展，但目前仍存在几方面的问题： 不能将噪声数据无缝的融入到已有算法中； 网格生成仍然很复杂； 由参数化偏微分方程控制的高维问题无法解决； 求解隐含物理的逆问题代价昂贵，通常需要不同的公式和复杂的代码。 机器学习方法在一定程度上可以解决上述问题，但是训练深度神经网络需要大量的数据，对于某些科学和工程问题，大量的数据意味着高昂的成本，在实际使用中并不具有有效性。 如何基于受限于成本的小样本数据
方程自己解（1）——物理信息神经网络（PINN）
热门推荐
Liu Feng's Blog
10-13 5万+
文章目录前言(一) 物理神经网络（PINN）解读1.1 PINN基本背景1.2 PINN算法描述 前言   最近正在看利用“深度学习”（大概吧，其实只是利用了neural network的自动微分特性（AD）），在看一些文章的同时，将文章中提到的开源代码用起来和复现一些基本方程求解能够加快我学习的进度，这里将持续贴出一些方程和代码的求解过程。当然非常希望同学和朋友们可以给我指出错误，最后如果能够坚持下去，这个系列的工作会分享到github，同时如果对各个开源程序有所帮助那就更好了！   由于会参考到很多文章
用 PINN（Physics-Informed Neural Networks）求解二阶Diffusion方程的PyTorch 代码
06-13
好的，以下是用 PINN 求解二阶 Diffusion 方程的 PyTorch 代码： ```python import torch import numpy as np import matplotlib.pyplot as plt # 定义求解区域的左右边界 x_left = 0.0 x_right = 1.0 # 定义时间和空间步长 delta_t = 0.001 delta_x = 0.05 # 定义神经网络的输入维度和隐藏层维度 input_dim = 2 hidden_dim = 10 # 定义神经网络的输出维度 output_dim = 1 # 定义 Diffusion 方程的初始条件和边界条件 def u_init(x): return np.sin(np.pi * x) def u_left(t): return 0.0 def u_right(t): return 0.0 # 定义神经网络模型 class PINN(torch.nn.Module): def __init__(self): super(PINN, self).__init__() self.fc1 = torch.nn.Linear(input_dim, hidden_dim) self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim) self.fc3 = torch.nn.Linear(hidden_dim, output_dim) def forward(self, x, t): # 拼接时间和空间坐标作为神经网络的输入 xt = torch.cat([x, t], dim=1) h1 = torch.tanh(self.fc1(xt)) h2 = torch.tanh(self.fc2(h1)) out = self.fc3(h2) return out # 定义 PINN 的损失函数 def pinn_loss(model, x_left, x_right, delta_t, delta_x): # 定义空间和时间的网格 x = torch.linspace(x_left, x_right, int((x_right - x_left) / delta_x) + 1).unsqueeze(1) t = torch.linspace(0, 1, int(1 / delta_t) + 1).unsqueeze(1) # 计算模型在内部网格点上的预测值 x_internal = x[1:-1] t_internal = t[1:-1] u_internal = model(x_internal, t_internal) # 计算模型在左右边界上的预测值 u_left_boundary = model(x_left, t_internal) u_right_boundary = model(x_right, t_internal) # 计算初始条件和边界条件的损失 init_loss = torch.mean((model(x, torch.zeros_like(x)) - u_init(x)) ** 2) left_boundary_loss = torch.mean((u_left_boundary - u_left(t_internal)) ** 2) right_boundary_loss = torch.mean((u_right_boundary - u_right(t_internal)) ** 2) # 计算 Diffusion 方程的残差 u_x = torch.autograd.grad(u_internal, x_internal, grad_outputs=torch.ones_like(u_internal), create_graph=True)[0] u_xx = torch.autograd.grad(u_x, x_internal, grad_outputs=torch.ones_like(u_x), create_graph=True)[0] f = u_xx - (1 / delta_t) * (u_internal - u_init(x_internal)) # 计算残差的损失 residual_loss = torch.mean(f ** 2) # 计算总的损失 loss = init_loss + left_boundary_loss + right_boundary_loss + residual_loss return loss # 初始化神经网络模型和优化器 model = PINN() optimizer = torch.optim.Adam(model.parameters(), lr=0.001) # 训练神经网络模型 for i in range(10000): optimizer.zero_grad() loss = pinn_loss(model, x_left, x_right, delta_t, delta_x) loss.backward() optimizer.step() if i % 1000 == 0: print("Iteration {}, Loss = {}".format(i, loss.item())) # 使用训练好的神经网络模型进行预测 x_test = torch.linspace(x_left, x_right, 101).unsqueeze(1) t_test = torch.linspace(0, 1, 1001).unsqueeze(1) u_test = model(x_test, t_test).detach().numpy() # 绘制预测结果 X, T = np.meshgrid(x_test, t_test) plt.pcolormesh(X, T, u_test, cmap='coolwarm') plt.colorbar() plt.xlabel("x") plt.ylabel("t") plt.title("PINN Solution to Diffusion Equation") plt.show() ``` 这段代码中，首先定义了求解区域的左右边界、时间和空间步长等参数，然后定义了 Diffusion 方程的初始条件和边界条件，以及神经网络模型和损失函数。在训练神经网络模型时，使用了 Adam 优化器，最后使用训练好的模型进行预测，并绘制了预测结果。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

pinn山里娃

原创不易请多多支持

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值