逆变器的输出外特性分析

shiyin2869351

已于 2023-05-06 16:07:32 修改

阅读量1.6k

点赞数 6

分类专栏：电力系统小嗨客文章标签：经验分享嵌入式硬件

于 2022-11-29 19:32:20 首次发布

本文链接：https://blog.csdn.net/weixin_45544709/article/details/128102697

版权

电力系统小嗨客专栏收录该内容

9 篇文章

订阅专栏

VSG 并网状态下，考虑到弱电网下线路阻抗不能忽略，VSG 的功率传输模型可以表示为 VSG 的输出电压经过线路阻抗后串联至电网（考虑滤波电感，且忽略滤波电容作用）。设 U 为 VSG 输出电压的幅值，Ug为电网电压的幅值，并将电网的相位视作基准相位，即相角为 0。则表示为输出电压 U 和电网电压 Ug之间相位差，类似于同步发电机中内电势和机端电压之间的功角。线路阻抗表示为 $Z\angle \Theta =R_{g}+jX_{g}$ 。VSG 的功率传输模型和矢量关系如图 1 和图 2所示。

图1 VSG的功率传输模型

图2 VSG功角矢量图

易知线路电流可表示为：

由此可以推导出 VSG 馈入电网的功率为：

公式（1-2）中，S 为复功率，为的共轭，Pe和 Qe分别为 VSG 馈入电网的有功功率和无功功率。将具体的线路阻抗参数带入上式则有功无功功率进一步可以表示为：

从式（1-3）可以看出 VSG 的输出的有功无功不仅和线路阻抗有关，还跟两侧的相位差有关。从 VSG 的输出功角特性可以看出功率的流向和电压降的方向有关，同时还反映出功率之间存在的耦合关系，针对不同的线路阻抗情况，需要选择不同的控制策略来消除耦合。下面依次针对线路阻抗呈纯感性，纯阻性和阻感性的情况来分析，且默认功角 $\delta$ 都比较小，则 $cos\delta =1,sin\delta =\delta$ , 。

当线路阻抗为纯感性时，即 $Z\angle 90^{\circ }=jX_{g}$ 时：

分别对上式求 $\delta$ 和 U 的偏导可得：

从式（1-5）中可以看出，有功功率 Pe 主要与功角变化相关，受输出电压影响较小，无功功率 Qe 完全受输出电压影响，与功角无关。实现了功率的解耦，并可以据此设计有功-频率和无功-电压的控制环节。

当线路阻抗为纯阻性时，即 $Z\angle 0^{\circ }=R_{g}$ 时：

分别对上式求 和 U 的偏导可得：

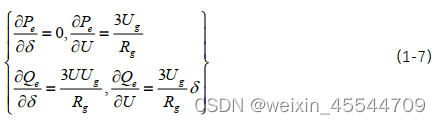
从式（1-7）中可以看出有功功率 Pe 完全受输出电压影响，不受功角变化的影响，无功功率 Qe 主要受功角影响，受输出电压影响较小。此时无法满足VSG 有功-频率和无功-电压的下垂特性要求。当线路阻抗为阻感性时，即 $Z\angle \Theta =R_{g}+jX_{g}$ 时：

分别对上式求 和 U 的偏导可得：

从式（1-9）中可以看出 VSG 输出的有功和无功功率与电压和功角均有较大耦合，不能直接实现 VSG 的有功调频和无功调压特性。针对弱电网下，线路阻抗无法忽略使输出的有功无功功率存在耦合的问题，可以利用 VSG 控制算法中的定子电气方程来添加虚拟电阻和虚拟电感，改变线路的等效参数，使逆变器输出端和电网之间的等效线路阻抗含有较多感性成分，优化阻感比，且保持较小功角，实现 VSG 的解耦控制，保证系统的稳定性。