PWM整流器双闭环PI参数的整定

1. 整流侧电路拓扑图

       整流电路由交流侧电源、线路电阻、线路电抗、整流器、滤波电容以及负载组成。整体电路图如图1所示。

图 1 整流电路拓扑图

其中，IGBT的开关状函数如下式所示

 

 根据图 1 列出 KVL 公式如下，电流的正方向是从左到右

对于每一相的IGBT相当于是半桥结构，对于单相而言，是遵循DC-DC变换器的基本规律。基于此，可令                                          

                  

由于ea+eb+ec=0、Ua+Ub+Uc=0，得到                                                                                      

 

将公式（3）带入公式（4）中可得                                    

整理得：                                                               

对直流侧分析                                                  

直流电容值为

                                                                                                      

再令uaN+uNO=uao=ua，同理可得到ub、uc

经过替换，公式（2）可以变成

                                                   

2. 双闭环控制器的设计
2.1 abc to dq

令变换系数为 B

 根据数学微分计算可知

 将上式整理得到

 同理，

将上式整理得到
 

 利用公式(10)、 (12)和(14)计算得到

将公式(15)整理得到

 由于 sinwt 是属于 d 轴上的量， coswt 是属于 q 轴上的量，所以通过观察上式不
难发现， d 和 q 轴之间存在耦合关系。

即

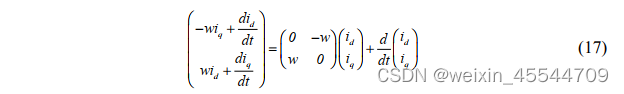
再将两侧乘以𝐿𝑠

将结合公式(18)和公式(9)可得

将上式拆开可得到：

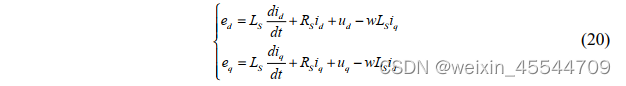
再对公式(20)进行拉氏变换可得（微信形式需要变为 S）：

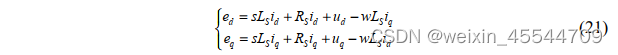
则 PWM 整流器的输入输出模型为

图 2 PWM 整流器的输入输出模型

2.2 电流内环的设计

利用公式进行变量替换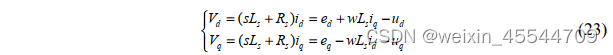

若将𝑉𝑑 = (𝑆𝐿𝑆 + 𝑅𝑠)𝑖𝑑形式变换为

则此公式的控制框图为

图 3 电流和电压的关系框图

在控制环中加入 PI 控制，可得

图 4 加入 PI 控制的电压和电流控制框图

图中， 𝐺𝑐(𝑠) = 𝐾𝑝 + 𝐾i/𝑆，从图中可得，

结合公式(23)和公式(25)可以得到

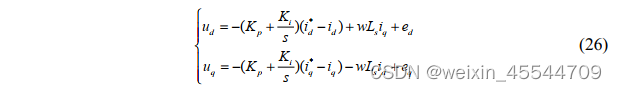
然后根据公式(26)可以设计出控制器的框图为

图 5 控制电路图

由图 5 可知，解耦过程如下；

通过上式可以看出，前后被消掉了，从而达到了解耦的目的， 解耦亦是如此。 图 5 中左侧即是电流内环的控制结构。

2.3 电压外环的控制设计

电压外环的控制是为了生成电流的参考值， 将直流测电压实际值与参考值进行对比，并经过 PI 控制之后得到的参考值， 其框图如图所示：
 

图 6 电压外环控制框图

3  双闭环 PI 控制参数的整定

3.1 电流内环的整定

电流内环可以按照 I 型系统和 II 型系统进行整定， I 型系统为

图7 I 型系统框图

II 型系统框图

图8 II 型系统框图

下面讨论三相 VSR 电流内环结构的参数的设计，要考虑电流内环的信号夏阳的延迟和 PWM 控制的小惯性特性，已解耦的电流内环控制结构图如图所示。
 

 图 9 已解耦的电流内环控制结构图

上图中的电流环负反馈图为
 

 图 10 iq 电流环结构图

 在图 10 中 Ts 为电流内环的采样周期（即 PWM 的开关周期）， KPWM为桥路 PWM等效增援，为简化分析，暂不考虑𝑒𝑞的扰动，且将 PI 调节器传递函数写成零极点的形式，即

 将小时间常数 Ts/2、 Ts 合并，得到简化的电流内环结构，结构如图所示

 图 11 无 eq 扰动时的 iq 电流内环简化结构图

3.2 电流调节器的设计
3.2.1设计方案 1——按典型 I 阶系统进行设计电路

当考虑电流内环需获取较快的电流跟随性时，可按照 I 型系统设计电流调节器， 从图 11 中可以看出，只需要以 PI 调节器零点抵消掉电流控制对象传递函数的极点即可，即𝜏𝑖 = 𝐿/𝑅,校正后，可得电流的开环传递函数为

由典型的 I 型系统参数整定关系，当取系统阻尼比𝜉 = 0.707时，有

 求解得

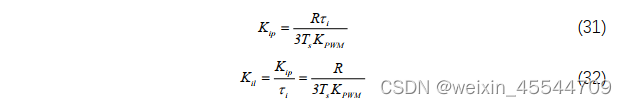
 公式(31)和(32)即为电流内环的比例积分系数值
另外，电流内环的闭环传递函数为

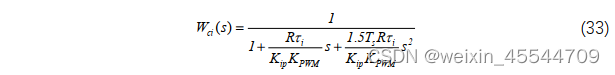
 由于开关频率足够高，则 Ts 也会足够小， 由于𝑠2的系数远小于 s 项的系数， 从而
 这一项可以忽略不计，

 

 将公式(31)带入(33)中可得，得到电流内环的等效传递函数为

 上式表明，当电流内环按照典型 I 型系统进行整定时，电流内环可近似为等效成一个惯性环节，其惯性时间常数为3𝑇𝑠，显然，开关频率足够高时候，电流内环具有较快的动态响应。

    当闭环控制系统的闭环增益减少至-3dB 或者其相位移为-45°时，该点频率可定义为闭环系统频带宽度𝑓𝑏。实际上，除了一阶惯性环节以外，控制系统-3dB个相位移-45°频率点并非在一个频率点上，这时期带宽应取；两频率点中较低者。对于典型 I 阶系统设计的三相 SVR 电流内环系统，由于电流内环可等效成一阶惯性环节，因而电流内环的频带宽度𝑓𝑏𝑖为

 式中： 𝑓𝑎为电流内环 PWM 的调制频率

对于阻尼比为𝜉 = 0.707的典型 I 阶系统的动态指标见表

表中， 𝜏为与典型 I 型系统开环传递函数节点对应的时间常数，且𝜏 = 1.5𝑇，显然电流内环具有良好的跟随性
I 型电流内环设计时，并没有考虑电网电动势𝑒𝑞扰动对输出的影响，当考虑𝑒𝑞的扰动时， 𝑒𝑞电流内环简化结构如图所示，

 图 12 𝑒𝑞的扰动时电流内环简化结构

为讨论电流内环的简化结构,令𝑖𝑞∗ = 0，则由上图可知， 其输出电流变化量为

 式中， W s ci ( ) 为电流内环等效闭环传递函数

考虑阶跃扰动，则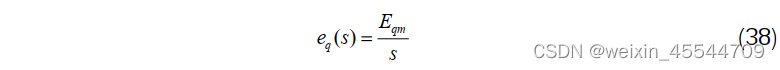

 E qm为阶跃扰动幅值

将公式(38)代入到(37)，且令阻尼比为𝜉 = 0.707，即，
这样

 利用部分分式法分解式(39)，再求拉式反变换，可得阶跃扰动时，输出变化量的时域表达式，即

 式中， m 为电流内环结构中， 𝑒𝑞扰动点两边传递函数中的市价常数之比，即。显然， 𝜏𝑖 = 𝐿/𝑅 > 1.5，即 m<1,若以∆𝑖𝑞𝑏 = 𝐸𝑚/(2𝑅)为基准值，计算出∆𝑖𝑞𝑚𝑎𝑥/∆𝑖𝑞𝑏其主要结果如表所示

 表 1 𝜉 = 0.707时电流内环抗扰性指标

 

 注： tm扰动输出最大降落时间； 𝑡𝑟误差带为±5%Δ𝑖𝑝ℎ时的扰动输出恢复时间

从表 1 中数值课看出，当电流内环结构中𝑒𝑞扰动点两侧对象时间常数相差较大时，动态降落减少，但恢复时间较长。三相 VSR 电流内环控制正属于这种情况，因此电流内环按典型 I 型系统设计时，虽然电流控制具有较好的跟随性能，但系统抗扰能力较差，为了改善电流内环的抗扰性能，可以开率采用典型的 II型设计。
3.2.2 设计方案 2——按典型 II 阶系统进行设计电路
        以上电流内环的抗扰性能不理想的主要原因是，当按照 I 型系统设计时，与电流源内环 PI 调节器中零点对应的时间常数𝜏𝑖 = 𝐿/𝑅和与典型 I 型系统开环传递函数极点对应的时间常数 1.5Ts 相比，其比值𝜏𝑖/(1.5𝑇𝑠)中频宽过大,为了提高电抗内环的抗扰性能，应该减小𝜏𝑖/(1.5𝑇𝑠)的比值（中频宽）。
            为了近似确定这种设计中的 PI 调节器的参数，当𝜔𝑐 ≫ 𝑅时（𝜔𝑐为电流环截止频率），可令(1/𝑅)/[(L/R) 𝑠 + 1] ≈ 1/𝐿𝑠,即忽略 VSR 交流侧电阻 R 时的电流内环控制结构如图所示

 图 13 忽略 R 时近似的电流内环结构

由此可按典型 II 型系统设计电流内环调节器，从图 13 得到电流内环的的开环传递函数为

为了尽量提高电流响应的快速性，对典型 II 型系统而言，可设计适当的中频带宽ℎ𝑖[ℎ𝑖 = 𝜏𝑖/(1.5𝑇𝑠)],工程上常数取ℎ𝑖 = 𝜏𝑖/1.5𝑇𝑠= 5。按照典型 II 型系统参数设计关系，得

 解得

 当按典型 II 型系统设计电流内环 PI 调节器参数时，中频带宽ℎ𝑖与跟随性指标以及与电流内环抗扰性能指标均有对应的关系

表 2 典型 II 阶系统阶跃输入跟随性指标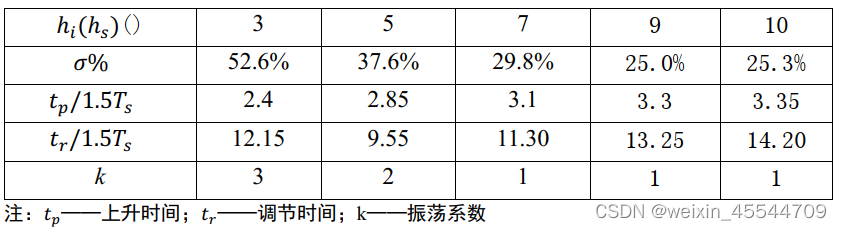

 表 3 典型 II 阶系统动态抗扰性指标

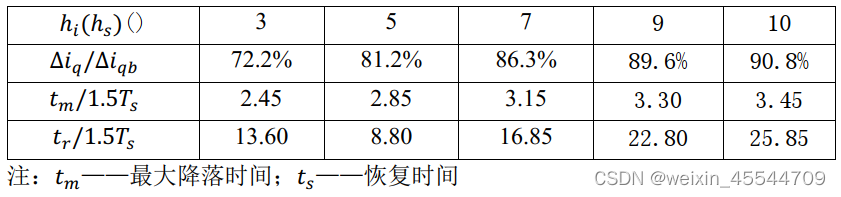
 从上表中关系分析，当典型的 II 阶系统设计控制策略时，中频带宽 h 越大，系统跟随控制时间超调越小，且抗扰性变弱，因此，系统跟随性与抗扰性之间设计存在一定的矛盾，工程上只能相互兼顾，实际上，电流内环按典型 II 型系统设计时，取ℎ𝑖 = 5就是兼顾控制系统的跟随性、抗扰性的具体体现。
         值得注意的是，上述典型 II 阶系统设计是一种近似设计，因为实际的电流控制对象是一阶惯性环节(𝑅1) /[(𝑅𝐿) 𝑠 + 1]，将其近似成一个积分环节，往往带来设计误差，当电流采样频率，即 PWM 开关频率𝑓𝑖足够高时，可恶意忽略电流内环等效小时间常数（1.5Ts）影响，此时，若电流内环仍采用 PI 调节器控制，其内环近似结构，如图所示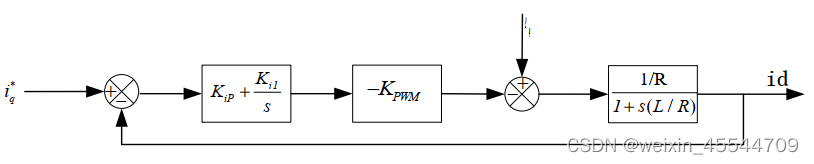

 图 14 忽略小时间常数近似时的电流内环结构

若不考虑 eq 的扰动，则由图可求得电流内环的闭环传递函数为

 公式中

 由公式(45)算得电流内环阻尼比𝜉和自然振荡频率𝜔𝑛为

联立公式(46)和(47)，计算得

当电流内环近似成一阶惯性环节时，电流内环频带宽度𝑓𝑏𝑖 = 𝑓𝑤/20,因此，工程中可取电流内环自然振荡频率𝜔𝑛 ≤ 2𝜋𝑓𝑤/20，阻尼比为𝜉 = 0.707，将𝜔𝑛和𝜉带入公式(48)，即可计算出电流内环的 PI 参数

3.2.3 电压外环的设计
电压外环控制的目的是为了稳定 PWM 整流器的整流侧电压𝑢𝑑，为简化控制系统的设计，当开关频率远高于电网电动势基波频率时，可忽略 PWM 谐波分量，经过推导可得，当不考虑负载扰动时，电压外环的简化结构如图所示，其中𝜏𝑣是电压采样小惯性时间常数， 𝑇𝑐𝑣 = 𝜏𝑣 + 3𝑇𝑠， 𝐾𝑣和𝑇𝑣分别为电压外环的 PI 调节器参数。

 图 15 电压外环简化结构

由于电压外环的主要控制作用是稳定直流侧电压，故可对进行控制系统设计时，应重点考虑其抗扰性能，可以按照典型 II 型系统进行设计
 

 图 16 典型 II 阶系统的结构

电压外环的开环传递函数为

 可得到电压外环的中频的带宽 h，为

 由典型 II 阶系统的控制器参数整定原则可知

 综合电压外环的抗扰性能和跟随性能，一般取中频带宽ℎ𝑣为 5，则可以以求得电压外环的调节器参数为