第七章 微分方程

已于 2022-05-04 22:19:26 修改
阅读量3.7k 收藏 20
点赞数 3
分类专栏： # 汤家凤基础班内容全收录 文章标签： 算法
于 2022-03-16 22:25:48 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_45564209/article/details/123538381
版权
本文详细介绍了微分方程的基本概念，包括一阶微分方程的解法，如可分离变量、齐次和非齐次类型，并探讨了可降阶的高阶微分方程。此外，还深入讲解了高阶线性微分方程的解的结构和性质，特别是常系数线性微分方程的解法。内容覆盖了解题技巧和实例分析，适合学习巩固微分方程知识。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

第一节 微分方程的基本概念

在这里插入图片描述

听了汤讲的稍微理解一下就行了，日后不断anki熟悉吧

第二节 一阶微分方程的种类及解法

一.可分离变量的微分方程

在这里插入图片描述
定义
在这里插入图片描述
解法

在这里插入图片描述

小例题，同时也注意一下那个tan的变化

在这里插入图片描述
这里就是需要注意一下你的定义域，你讨论的时候需要在意的，你像分母这种东西不能为0要注意的，但是他说以后直接除？？不用讨论，不懂，这里先放掉

二.齐次微分方程

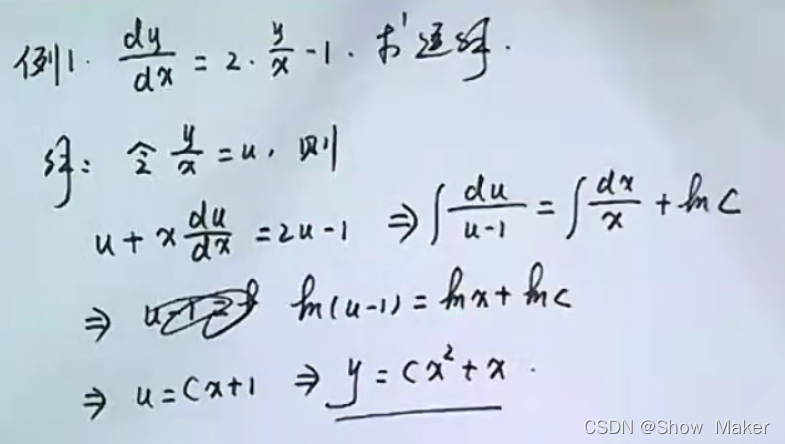
在这里插入图片描述
定义
在这里插入图片描述

  • 令
  • 变量分离
  • 积分在这里插入图片描述

那个不+C加lnC的技巧
在这里插入图片描述

好题

三.一阶齐次线性微分方程

在这里插入图片描述
P（x）可以是常数也可以是x的表达式

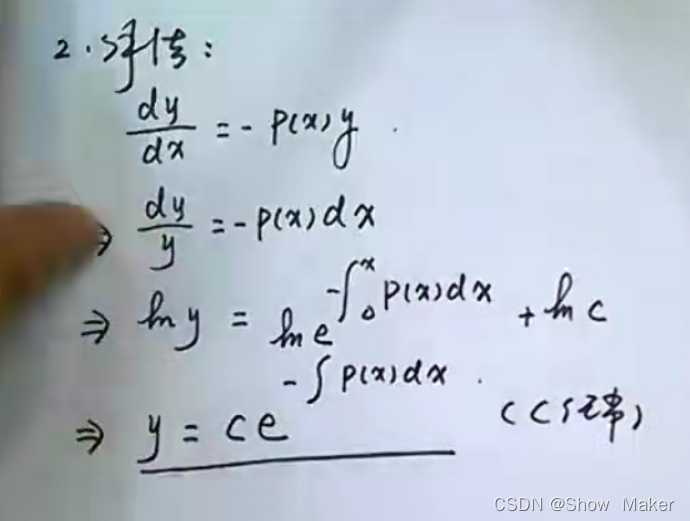
在这里插入图片描述
解法：需要同时记住推导和结论
在这里插入图片描述
这题用一阶齐次线性微分方程做
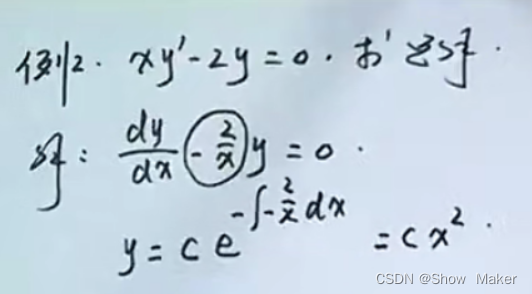
在这里插入图片描述

代公式，很方便
在这里插入图片描述

四.一阶非齐线性微分方程

一阶
在这里插入图片描述
通解公式

在这里插入图片描述
推导过程：常数变易法，推导过程的一部分，看看就好

在这里插入图片描述
可以，好题
在这里插入图片描述
只能说巧得不能再巧了，就是你不定积分的公式要弄熟练就好做了

第三节 可降阶的高阶微分方程

除了1阶，其他全部都算高阶

1.形如y(n) = f(x)的方程

在这里插入图片描述
在这里插入图片描述

你告诉我，这种可降解的高阶他不无聊嘛，没用的——汤家凤

2.形如f(x,y’,y’') = 0的方程（缺y型）

在这里插入图片描述

就这么简单，吼，就这么简单~——汤家凤
在这里插入图片描述

3.形如f(y,y’,y’') = 0的方程（缺x型）

在这里插入图片描述
化为的式子的原因
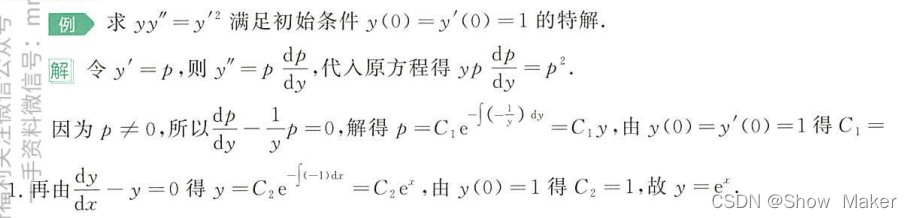
在这里插入图片描述
解法

在这里插入图片描述
好题，内容挺多的，需要对前面的公式很熟练

第四节 高阶线性微分方程

一.高阶线性微分方程的基本概念

1.n阶齐次线性微分方程

在这里插入图片描述

2.n阶非齐次线性微分方程

在这里插入图片描述

二.高阶线性微分方程解的结构与性质

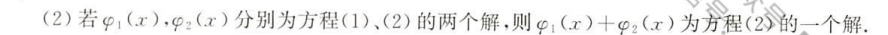
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

三.高阶常系数线性微分方程

1.二阶常系数齐次线性微分方程的解法

在这里插入图片描述

在这里插入图片描述
好了，就这么简单
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

1.二阶常系数非齐次线性微分方程的特解

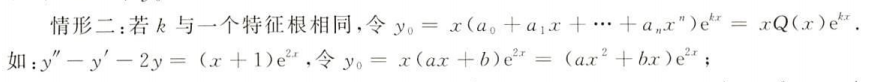
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
第一步
在这里插入图片描述
第二步
在这里插入图片描述
在这里插入图片描述
好做得一塌糊涂啊
在这里插入图片描述
在这里插入图片描述
小技巧，那个地方求二阶导数

缺少部分参数的微分方程拟合之一
Lu的专栏
07-31 393
问题来源：如何拟合微分方程组的参数？ – MATLAB中文论坛 (ilovematlab.cn) 微分方程组如下： dx/dt=a*x-b*x*y dy/dt=-c*y+d*x*y 数据如下： t x(t) y(t) 11 45.79 41.40 12 53.03 38.90 13 64.05 36.78 14 75.40 36.04 15 90.36 33.78 16 107.14 35.40 17 127.79 34.68 18 150.77 36.61 19 179.65 37.71 20 ..
【高数】高阶可降阶微分方程的解法？什么时候考虑把dx/dy换元（反函数高阶导数）？
多学，多想，多总结
09-11 7147
高阶可降阶微分方程问题：缺y项的微分方程如何求解？换元时y''=dp/dx，还是y''=p·dp/dx？ 反函数高阶导数：什么时候将x看作y的函数呢？
第七章——微分方程
naozibuok的博客
06-18 9612
齐次”的含义就是次数相等，y''+py'+qy=0都是一次幂，所以是齐次线性微分方程，如果说加上一个常数c，变为y''+py'+qy+c=0，那么这个c是可以看作cy⁰，y的零次幂，就不是齐次微分方程了。例3：y'+y/x=sinx/x，y|x=π=1的特解。例2：求y'=e^2x-y，y|x=0=0的特解。例1：求(1+x^2)y''=2xy'的通解。例子2：求y''-2y'-3y=0的通解。例子3：求y''-2y'+5y=0的通解。例2：求yy''-y'^2=0的通解。例1：求y'=y的通解。
2011考研数学二第（4）题——二阶微分方程
qq_44292038的博客
07-13 313
微分方程的来龙去脉
Caesar2334的博客
11-27 1415
（2）除了上述两个方面的全设置之外，额外再说一个小特点，即考研要求的两种特解的情况可能与与上面的三种特征方程会一起混用，即当特解设置的是关于sinx和cosx的共轭复根的时候，特征方程可能不是共轭复根，这个时候就可以选择不是共轭复根的选项，使得k = 0就好了。值得一提的是通解的设定：有三种情况，有特征方程求出的三种情况，不相同的根，相同的重根，共轭复根，这三种是独立的体系，不相同的根使用用于一个体系，首先很多人疑惑微分方程中特解的问题？（6）说到微分方程的，一定离不开导数和微分之间的关系，需要明确的是，
常微分方程及其基本例题
qq_16183037的博客
01-11 7107
文章目录零 基本概念微分方程向量场一 可分离变量1.1 变量分离1.2 变量变换1.3 齐次微分方程二 一阶微分方程2.1 齐次线性2.2 非齐次线性三 伯努利微分方程3.1 定义3.2 解法四 恰当微分方程4.1 定义4.2 解法五 积分因子5.1 定义5.2 解法六 可降阶微分方程6.1 缺y型6.2 缺x型七 高阶微分方程7.1 定义与解结构7.2 常系数齐次7.3 常系数非齐次7.4 欧拉方程八 关于解8.1 存在唯一性8.2 朗斯基行列式九 重点题型9.1 基础类型9.2 常系数类9.3 非特定型
第七章 微分方程1
08-03
本章主要探讨了一阶微分方程的解法。一阶微分方程可以分为多种类型，如分离变量型、线性型、伯努利方程等。 首先，我们来看第一类问题，即求一阶微分方程的通解。例如，题目中的(1)题，通过变换变量将方程转换为...
第七章 微分方程复习课1
08-08
总结来说，本章复习涵盖了微分方程的基本概念、解法，特别是变量可分离的微分方程和一阶线性微分方程的解法，以及二阶常系数线性微分方程的处理。理解和掌握这些知识对于解决实际问题和深入学习微分方程理论是至关...
高数第七章微分方程.pdf
03-11
同济版考研高数第7章
高等应用数学问题的MATLAB求解 第7章 微分方程问题的计算机求解 共130页.pptx
最新发布
11-10
第7章 微分方程问题的计算机求解 共130页.pptx 第8章 数据插值、函数逼近问题的计算机求解 共100页.pptx 第9章 概率论与数理统计问题的计算机求解 共104页.pptx 第10章 数学问题的非传统解法 共147页.pptx
第7章 微分方程数值解.ppt
07-30
第7章 微分方程数值解.ppt
不含一阶导数项的线性二阶微分方程的通解
weixin_57997461的博客
05-27 766
连续的,如果有人倾向于推广，在相对假弱的假设下，这个结果能够被发现。能够被任意非零的常数乘，它是可能的来归一化这些常值使其满足。是该线性二阶微分方程的特解，于是，整个问题的解可以写为。代表线性方程（2）的线性独立解，并且满足（4）式。引入一个新的函数，让我们联想到朗斯基行列式，但是与。是下列其次线性方程的任意两个线性无关的解。的朗斯基行列式被定义为。代入（1）式，可以得到。
微分方程的求解方法
热门推荐
Spuer_Tiger
12-13 15万+
文章目录前言Ⅰ.首先介绍一些关于微分方程的概念Ⅱ.在考研范围内的微分方程有哪几类Ⅲ.微分方程的求解方法1.一阶微分方程的求解①可分离变量型的解法②齐次型的解法③一阶线性型的解法（重难点）2.二阶可降阶微分方程的求解3.高阶常系数线性微分方程的求解 前言 本文主要介绍了考研范围的微分方程的求解类型及对应的求解方法，主要内容参考自张宇《闭关修炼》，希望本文对您有所帮助。 Ⅰ.首先介绍一些关于微分方程的概念 一阶是什么： 一阶微分方程就是指只有一阶导数或微分的微分方程。（注：阶数是微分方程中含有的导数或微分的
7.5 可降阶的高阶微分方程
pikachu_12138的博客
11-17 1万+
本篇内容总结可降阶的高阶微分方程。 可降阶的高阶微分方程的分类 y(n)=f(x) (n≥2) ，y的高阶导数是一个关于x的函数； f(x,y’,y’’)，有x，有y’，有y’’，就是没有y； f(y,y’,y’’)，有y，有y’，有y’，'就是没有x； Case1:y(n)=f(x) (n≥2) 此类微分方程的解法没什么技术含量，就是一阶一阶往下降 例题 Case2:f(x,y’,y’’) 例1 例2 Case3: f(y,y’,y’’) 例1 总结 三种可降阶的高阶微分方程 第一种纯x，一
高数总结（微分方程）
三人行必有我师,手写三行必有所悟
02-03 3万+
1）微分方程：未知函数，未知函数的导数，自变量；2）微分的阶：最高阶导数的次数；3）可分离变量的微分方程：g(y)dy=f(x)dx型，这类微分方程的解法是两边同时积分；需要注意的是，虽然可以化为这种类型，但不一定能求出解的。4）齐次微分方程：可化为dy/dx=G(y/x)的方程。可令u=y/x，并变换成可分离变量的微分方程来求解；5）可化为齐次微分方程：dy/dx=(ax+by+c)/(lx+m
【微分方程】工科解常微分方程方法与公式集合
lafea的博客
03-20 2182
文章目录#一阶经典法##可分离变量型##不可分\齐次##一阶线性微分方程#二阶经典法##可降阶二阶##二阶常系数齐次线性微分方程##二阶常系数非齐次线性微分方程#微分算子法 D 求特解#积分变换解微分方程 欢迎纠错 #一阶经典法 ##可分离变量型 f1(x) dx=f2(y) dy∫f1(x) dx=∫f2(y) dy f_1(x)\space dx=f_2(y)\space dy\\ \int f_1(x)\space dx=\int f_2(y)\space d
【高数】如何由解倒求微分方程？及微分方程的阶数、任意常数、特征根的关系
多学，多想，多总结
09-09 1万+
微分方程的阶数、任意常数个数、特征根个数的关系，以及由解倒求各种类型微分方程的方法：倒推法、行列式法、特解代入法、消C法、综合法。
大学高数常微分方程思维导图_高等数学各章节知识点框架 常微分方程.pdf
weixin_35661054的博客
01-12 3060
【微信公众号：给力考研资料】免费分享常微分⽅程1.概念，2.⼀阶微分⽅程求解 3.⾼阶微分⽅程求解 4.应⽤题1.概念(7个概念，了解即可)微分⽅程—含有未知函数的导数或者微分的⽅程常微分⽅程—未知函数为⼀元函数的微分⽅程偏微分⽅程—未知函数为多元函数的微分⽅程微分⽅程的阶—未知函数的导数的最⾼阶数为⽅程的阶数微分⽅程的解—将函数代⼊⽅程，为恒等式，则该函数为解微分⽅程的通解与特解—通解—解中独⽴...
3 非齐次线性微分方程与无量纲化
yahhqy的博客
06-17 4498
0.引言   本节研究常系数二阶线性方程右边加入非齐次项的情况。非齐次项包括指数函数，三角函数或多项式函数的情况。 1.求解步骤   对于非齐次线性二阶ODEx¨+p(t)x˙+q(t)x=g(t)(1)\ddot{x}+p(t) \dot{x}+q(t) x=g(t)\tag{1}x¨+p(t)x˙+q(t)x=g(t)(1) g(t)≠0g(t)\neq 0g(t)​=0，其求解分3步 求对应齐次方程通解xh(t)=c1x1(t)+c2x2(t)x_{h}(t)=c_{1} x_{1}(t)+c_{
《常微分方程第三版》答案解析指南
7. 特殊函数：在求解某些类型的常微分方程时，会用到一些特殊的函数，如贝塞尔函数、勒让德多项式等。本部分介绍了这些特殊函数的性质和使用。 高等教育出版社的这本《常微分方程第三版答案》配备了详尽的习题答案...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值