电力电子技术（11）——变压器漏感对整流电路的影响、电容滤波

最新推荐文章于 2024-06-05 18:56:32 发布

欲读万卷书，不入愚昧途

最新推荐文章于 2024-06-05 18:56:32 发布

阅读量1.2w

点赞数 5

分类专栏：电力电子技术笔记文章标签：硬件工程学习

本文链接：https://blog.csdn.net/weixin_45589295/article/details/124378618

版权

本文详细探讨了变压器漏感在整流电路中的作用，解释了换相重叠角的概念及其计算，并阐述了其对不同整流电路的影响，包括电压平均值的降低和换相压降的产生。此外，还介绍了电容滤波在不可控整流电路中的应用，特别是单相和三相桥式电路的工作原理和关键数量关系。分析表明，漏感和滤波电容能改变电路的工作状态，影响晶闸管的开通特性和输出电压质量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2.3 变压器漏感对整流电路的影响

考虑包括变压器漏感在内的交流侧电感的影响，该漏感可用一个集中的电感 $\large L_{B}$ 表示。

以三相半波为例，然后将其结论推广。

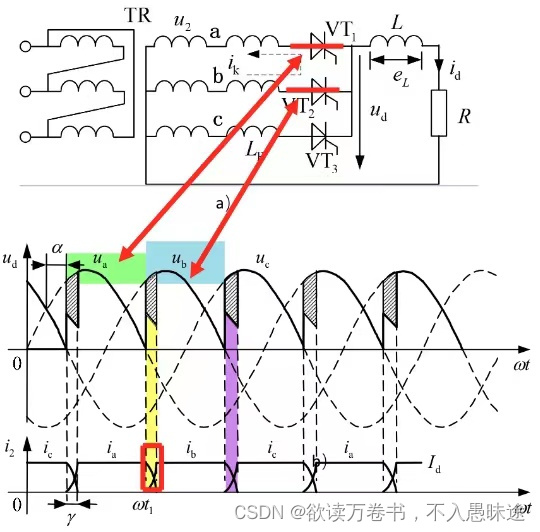
$\large VT_{1}$ 换相至 $\large VT_{2}$ 的过程：

因a、b两相均有漏感，故 $\large i_{a}$ 、 $\large i_{b}$ 均不能突变。于是 $\large VT_{1}$ 和 $\large VT_{2}$ 同时导通，相当于将a、b两相短路，在两相组成的回路中产生环流 $\large i_{k}$ 。

$\large i_{k}=i_{b}$ 是逐渐增大的，而 $\large i_{a}=I_{d}-i_{k}$ 是逐渐减小的。

当 $\large i_{k}$ 增大到等于 $\large I_{d}$ 时， $\large i_{a}=0$ ， $\large VT_{1}$ 关断，换流过程结束。

换相重叠角——换相过程持续的时间，用电角度 $\large \gamma$ 表示。

换相过程中，整流电压 $\large u_{d}$ 为同时导通的两个晶闸管所对应的两个相电压的平均值。

$\large u_d = u_a+L_B\frac{di_k}{dt}=u_b-L_B\frac{di_k}{dt}=\frac{u_a+u_b}{2}$

换相压降——与不考虑变压器漏感时相比， $\large u_d$ 平均值降低的多少。

$\large \Delta U_d=\frac{1}{2\pi /3}\int_{\alpha +\frac{5\pi }{6}}^{\alpha +\gamma +\frac{5\pi }{6}}(u_b-u_d)d(\omega t)=\frac{3}{2\pi }\int_{\alpha +\frac{5\pi }{6}}^{\alpha +\gamma +\frac{5\pi }{6}}[u_b-(u_b-L_B\frac{di_k}{dt})]d(\omega t)=\frac{3}{2\pi }\int_{\alpha +\frac{5\pi }{6}}^{\alpha +\gamma +\frac{5\pi }{6}}L_B\frac{di_k}{dt}d(\omega t)=\frac{3}{2\pi }\int_{0}^{I_d}\omega L_Bdi_k=\frac{3}{2\pi }X_BI_d$