反馈放大电路

反馈的基本概念和判断方法

• 正负反馈: 如果反馈到输入回路的信号和原来的输入信号作用相同, 二者叠加使放大电路净输入增加, 称这样的反馈为正反馈, 反之是负反馈.
• 电压反馈和电流反馈: 反馈信号取自输出电压则为电压反馈, 反馈信号取自输出电流成为电流反馈, 电压反馈可以稳定输出电压(降低输出电阻), 电流反馈可以稳定电流(增加输出电阻)
• 串联反馈和并联反馈: 若反馈信号在输入端与输入信号进行串联求和, 成为串联反馈, 反之是并联反馈. 如果信号源内阻较大, 应采用并联反馈, 反之若信号源内阻较小则适合串联反馈.
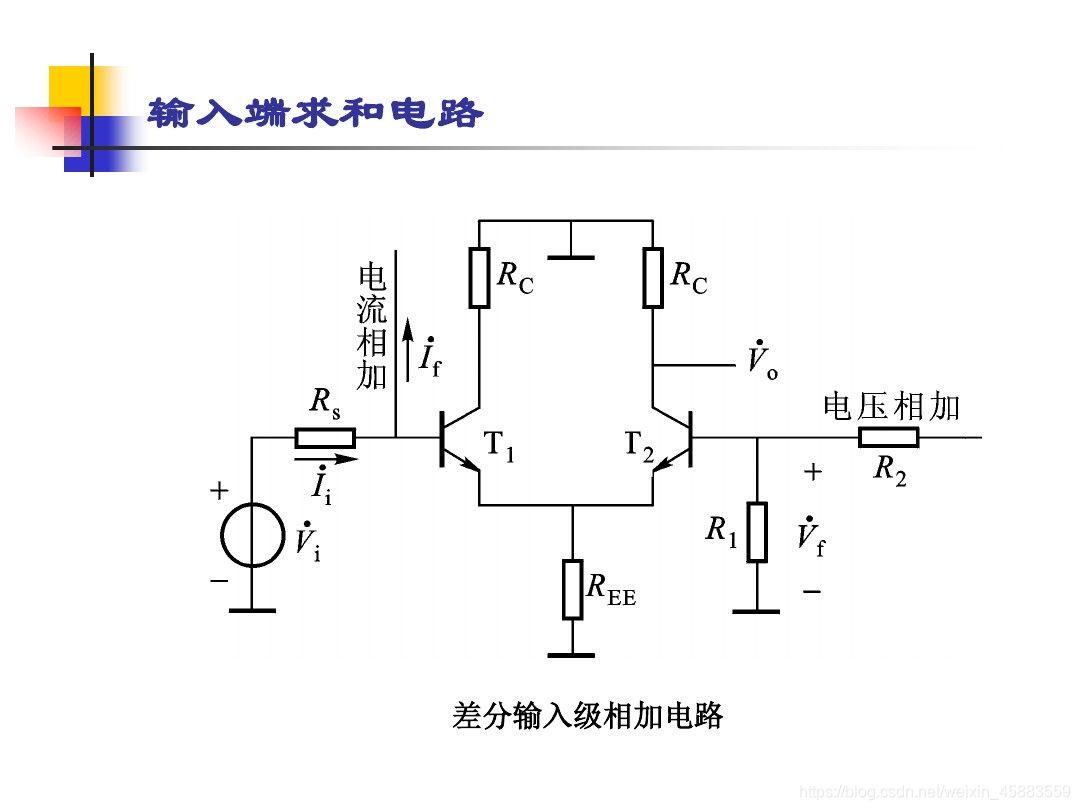
• 反馈极性的判断: 先假定输入信号的瞬时极性, 再确定输出量的极性, 再确定反馈量的极性, 再判断反馈量与原输入量对净输入的作用.
  
• 反馈基本方程式:
  闭环增益: $A_f$, 源增益:$A_{sf}$, 开环增益:$A$
  $$\begin{gathered} A_f=\frac{X_f}{X_o} \\ {\dot{A}}_f=\frac{X_o}{X_i}=\frac{X_o}{X_{i}d+X_f}=\frac{X_o}{X_{id}+F{X}_o}=\frac{A{X}_{id}}{X_{id}+AF{X}_{id}} \\ {A}_f=\frac{A}{1+AF} \\ {A}_{sf}=\frac{X_o}{X_s}=K{A}_f \end{gathered}$$
• 反馈深度: 根据反馈基本方程式, $|1+\dot{A}\dot{F}|$越大, 闭环增益下降的越多, 令$D=1+\dot{F}\dot{A}$, 称$\dot{D}$为反馈深度. 深度反馈下${\dot{A}}_f=\frac{1}{\dot{F}}$
• 环路增益: $$\frac{X_f}{X_{id}}=\dot{A}\dot{F}$$
  $\dot{A}\dot{F}$称为环路增益.

负反馈放大电路稳定性分析

• 自激振荡产生的原因: 在中频区引入负反馈时, ${\dot{X}}_f$和${\dot{X}}_i$同相, $\dot{A}\dot{F}>0$,此时${\phi }_A+{\phi }_F=2n\pi$, 反馈信号,输入信号, 净输入信号的关系为$|{\dot{X}}_{id}|=|{\dot{X}}_i|-|{\dot{X}}_f|$.
  由于耦合电容, 旁路电容及结电容的影响, $\dot{A}\dot{F}$产生滞后相移, 如果某一时刻该附加相移达到$180^o$, ${\dot{X}}_i$和${\dot{X}}_f$变成反相, 负反馈变成正反馈.
• 稳定性判别: 当$$\{\begin{array}{l}|\dot{A}\dot{F}|=1\\ |\Delta {\phi }_A+\Delta {\phi }_F|<180^o\end{array}$$或$$\{\begin{array}{l}|\dot{A}\dot{F}|<1\\ |\Delta {\phi }_A+\Delta {\phi }_F|=180^o\end{array}$$
• 增益裕度: 当$f=f_0$时, $\dot{A}\dot{F}$的附加相移达到$|180^o|$度, 所对应的增益称为增益裕度, 记为$$G_m=20\lg |\dot{A}\dot{F}|$$
  对于负反馈放大电路 ,增益裕度一般小于0, 且$G_m$越大, 电路越稳定, 一般要求$G_m<-10dB$
• 相位裕度: 当$f=f_c$时, $20\lg |\dot{A}\dot{F}|=0$,此时$|{\phi }_A+{\phi }_F|$与$180^o$的差称为相位裕度, 记为$${\phi }_m=180^o-|\phi (f_c)|$
  对于负反馈放大电路, ${\phi }_m>0$, 且${\phi }_m$越大, 电路越稳定, 一般要求${\phi }_m\ge 45^o$
• 分析方法: 利用基本放大电路的开环增益波特图来分析, 假设反馈网络为纯阻性的, 即${\phi }_F=0$, 自激振荡的幅值条件为$|\dot{A}\dot{F}|=1$,即$|\dot{A}|=|\frac{1}{\dot{F}}|$, 这样就可以在$20\lg |\dot{A}|$上绘出一条$20\lg \frac{1}{\dot{F}}$的水平线, 称为反馈线. 观察该点的附加相移大小即可判断放大电路稳定性.