关于本笔记的说明: 最好跟着 原书 整理个人笔记,他人笔记仅适合参考部分内容。
————————
高翔博客链接
百度网盘链接:https://pan.baidu.com/s/1VsrueNrdqmzTvh-IlFBr9Q
提取码:vfhe
《视觉SLAM十四讲》V2 2019年


动态定位和环境建模
SLAM 同时定位与地图构建
SLAM Simultaneous Localization and Mapping 同时定位与地图构建
搭载特定传感器的主体,在没有环境先验信息的情况下,于运动中建立环境的模型,同时估计自己的运动。
SLAM系统: 视觉里程估计、后端优化、建图、回环检测。
通过一番努力,看到事情顺利进行。


机器人本体: 轮式编码器、相机、激光传感器、惯性传导单元(Inertial Measurement Unit, IMU)。
- 对环境无要求
环境中: 导轨、二维码标志
单目SLAM只能估计相对大小关系, 估计的轨迹和地图 与真实的轨迹和地图 相差一个因子 尺度。 但仅有单目无法确定这个Scale的值。
单目的缺点:
1、需要平移后才能 计算深度
2、无法确定真实尺度。
有了距离信息, 场景的三维结构就可以通过单个图像恢复,同时消除尺度不确定性。
人眼 通过 左右眼图像的差异 来 判断物体的远近。
双目 的不足: 计算量很大
1、配置与标定 复杂,深度量程和精度受双目的基线和分辨率所限。
2、视差的计算非常消耗计算资源。
深度相机: 物理测距 发射光并接收返回的光,测出物体与相机之间的距离。

RGB-D不足: 主要用于室内
1、测量范围窄
2、噪声大
3、视野小
4、易受日光干扰
5、无法测量透射材质等
2.2 经典视觉 SLAM框架
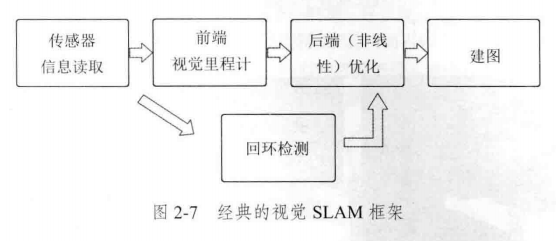
视觉里程计: 通过相邻帧的图像估计相机运动,并恢复场景的空间结构
里程计: 只计算相邻时刻的运动,与过去的信息没有关联。
已可实现:
1、一个视觉里程计, 估计两张图像间的相机运动
2、把相邻时刻的运动“串”起来 ——>获得 机器人的运动轨迹——> 实现 定位
3、根据每个时刻的相机位置,计算各像素对应的空间点的位置 ——> 地图
新的问题:
累积漂移 ——> 地图不一致
解决办法:
1、回环检测: 检测 机器人 是否 回到原始位置
- 计算机视觉 图像的特征提取与匹配
2、后端优化: 根据 回环检测 的信息,校正 轨迹形状
- 处理 噪声
- 滤波与 非线性优化算法
SLAM本质: 对 运动主体自身 和 周围环境空间 不确定性 的估计。
回环检测: 判断图像的相似性,让机器人确定自己回到了 之前经过的地方。 填补 漂移值
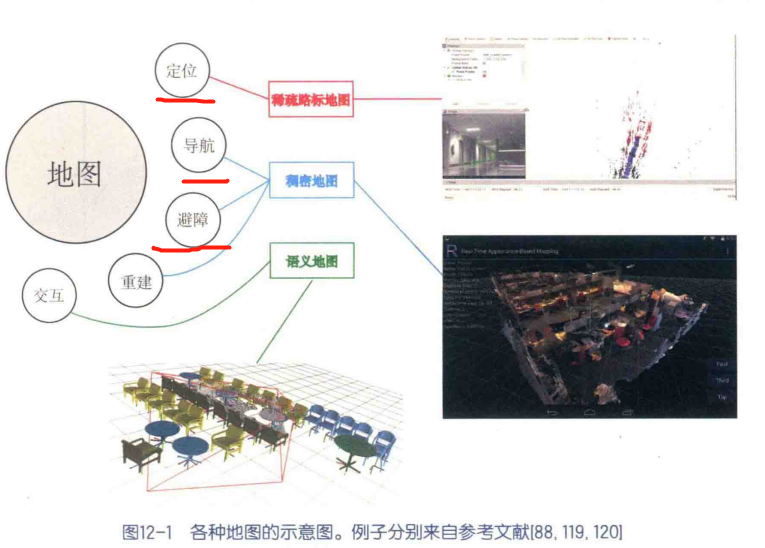
度量地图(Metric Map):
精确地表示 地图中物体的位置关系
稀疏只选择一部分有代表意义的物体(路标 Landmark) 定位
稠密 导航 (A*、D*)
拓扑地图(Topological Map)
强调地图元素之间的关系 考虑结点间的连通性
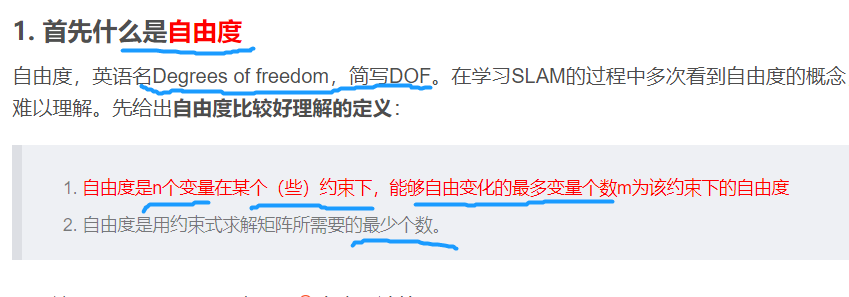
位姿由两个位置和一个转角描述时的运动方程:
[ x 1 x 2 θ ] k = [ x 1 x 2 θ ] k − 1 + [ Δ x 1 Δ x 2 Δ θ ] k + w k \begin{bmatrix} x_1\\ x_2 \\ θ \end{bmatrix}_k = \begin{bmatrix} x_1\\ x_2 \\ θ \end{bmatrix}_{k-1} + \begin{bmatrix} Δx_1\\ Δx_2 \\ Δθ \end{bmatrix}_{k} + \bm{w_k} x1x2θ k= x1x2θ k−1+ Δx1Δx2Δθ k+wk
携带二维激光传感器 观测方程
能测到的量: 路标点与机器人之间的距离 r r r 和夹角 ϕ \phi ϕ
路标点
y i = [ y 1 y 2 ] j T \bm{y_i}= \begin{bmatrix} y_1\\ y_2 \end{bmatrix}_j^T yi=[y1y2]jT
位姿
x k = [ x 1 x 2 ] k T \bm{x_k}= \begin{bmatrix} x_1\\ x_2 \end{bmatrix}_k^T xk=[x1x2]kT
观测数据
z k , j = [ r k , j ϕ k , j ] T \bm{z_{k,j}}= \begin{bmatrix} r_{k, j}\\ \phi_{k, j} \end{bmatrix}^T zk,j=[rk,jϕk,j]T
观测方程:
[ r k , j ϕ k , j ] = [ ( y 1 , j − x 1 , k ) 2 + ( y 2 , j − x 2 , k ) 2 a r c t a n ( y 2 , j − x 2 , k y 1 , j − x 1 , k ) ] + v \begin{bmatrix} r_{k, j}\\ \phi_{k, j} \end{bmatrix}= \begin{bmatrix} \sqrt{(y_{1,j}-x_{1,k})^2 + (y_{2, j}-x_{2,k})^2}\\ arctan(\frac{y_{2, j} - x_{2, k}}{y_{1, j}-x_{1,k}}) \end{bmatrix} + \bm{v} [rk,jϕk,j]=[(y1,j−x1,k)2+(y2,j−x2,k)2arctan(y1,j−x1,ky2,j−x2,k)]+v
运动方程和观测方程
{ x k = f ( x k − 1 , u k , w k ) , k = 1 , . . . , K z k , j = h ( y j , x k , v k , j ) , ( k , j ) ∈ O \left\{ \begin{aligned} \bm{x_k} & = f(\bm{x_k-1}, \bm{u_k}, \bm{w_k}), k = 1, ..., K\\ \bm{z_{k,j}} & = h(\bm{y_j, \bm{x_k, \bm{v_{k,j}}}}), (k, j)∈ \mathcal{O} \end{aligned} \right. {xkzk,j=f(xk−1,uk,wk),k=1,...,K=h(yj,xk,vk,j),(k,j)∈O
最基本的SLAM问题:
已知运动测量的读数 u \bm{u} u、传感器的读数 z \bm{z} z
求解: 定位问题 估计 x \bm{x} x; 建图问题 y \bm{y} y
状态估计问题:通过带有噪声的测量数据,估计内部隐藏的状态变量。
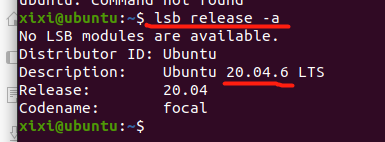
HelloSLAM
查看 ubuntu 版本 lsb_release -a
lsb_release -a
// helloSLAM.cpp
#include <iostream>
using namespace std;
int main( int argc, char** argv )
{
cout<<"Hello SLAM!"<<endl;
return 0;
}
在.cpp文件所在目录 打开命令行窗口,输入:
g++ helloSLAM.cpp
./a.out


g++ 默认将源文件编译成 名为a.out 的程序
cmake + make
ubuntu + 安装搜狗输入法【注意开始的中文选择,以及最后添加搜狗时去掉 仅显示系统语言的选择】
CMakeLists.txt: 告诉 cmake 要对这个目录下的文件做什么事情
# 声明要求的cmake 最低版本
cmake_minimum_required(VERSION 2.8) # 一般设为这个就行
# 声明一个 cmake 工程
project(HelloSLAM)
# 添加一个可执行程序 add_executable(程序名 源代码文件)
add_executable(helloSLAM helloSLAM.cpp)
在 CMakeLists.txt 所在 目录打开命令行窗口【Alt + Ctrl + T】
mkdir build
cd build
cmake..
make
./helloSLAM
执行cmake: 处理了工程文件之间的关系
执行make: 调用了 g++ 来编译程序
新建一个 中间文件夹 build 来 存放中间文件。
- 发布源代码时, 将build文件夹删掉即可
VS Code 自己下包安装,不要apt-get ,这样安装的Code无法使用中文输入
- 运行代码 前 记得 保存下代码



软件安装指令 sudo dpkg -i 安装包名
在安装包所在路径打开 命令行窗口
sudo dpkg -i 安装包名
用cmake 生成库
libHelloSLAM.cpp
//这是一个库文件
#include <iostream>
using namespace std;
void printHello() // 没有main函数, 无可执行文件
{
cout<<"Hello SLAM"<<endl;
}
CMakeLists.txt 里增加这行
# 建库
add_library(hello libHelloSLAM.cpp) ## 静态库
#add_library(hello_shared SHARED libHelloSLAM.cpp) ## 共享库 节省空间
静态库:.a 每次调用都会生成一个副本
共享库:.so 只有一个副本 更省空间

cmake .. 空格不能少
编写头文件.h
libHelloSLAM.h
#ifndef LIBHELLOSLAM_H_
#define LIBHELLOSLAM_H_
// 上面的宏定义是为了防止重复引用这个头文件而引起的重定义错误
void printHello(); // 打印一句 Hello 的函数
#endif
函数调用 示例:
useHello.cpp
#include "libHelloSLAM.h"
// 使用 libHelloSLAM.h 中的 printHello() 函数
int main( int argc, char** argv )
{
printHello();
return 0;
}
CMakeLists.txt 增加 链接 指令:
# 声明要求的cmake 最低版本
cmake_minimum_required(VERSION 2.8) # 一般设为这个就行
# 声明一个 cmake 工程
project(HelloSLAM)
# 添加一个可执行程序 add_executable(程序名 源代码文件)
add_executable(helloSLAM helloSLAM.cpp)
# 建库
add_library(hello_shared SHARED libHelloSLAM.cpp) ## 生成 共享库
############ 增加 链接 指令
add_executable (useHello useHello.cpp)
target_link_libraries(useHello hello_shared) ## 这里用的共享库
cd build
cmake ..
make
./helloSLAM

第3讲 三维空间 刚体运动
旋转 + 平移
基: 张成 这个空间 的一组线性无关的量
内积: 点乘 向量间 的投影关系
外积: 叉乘 两个向量张成的四边形的面积。
a^ 相当于 a叉乘
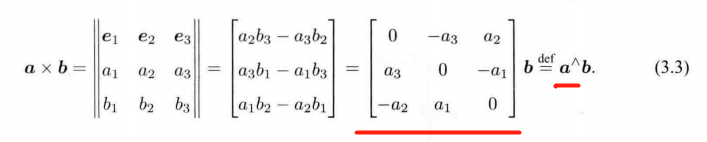

反对称矩阵 (Skew-symmetric Matrix): 为了实现 叉乘 转 点乘的转换
刚体运动: 两个坐标系之间的运动由一个旋转加上 一个平移组成。
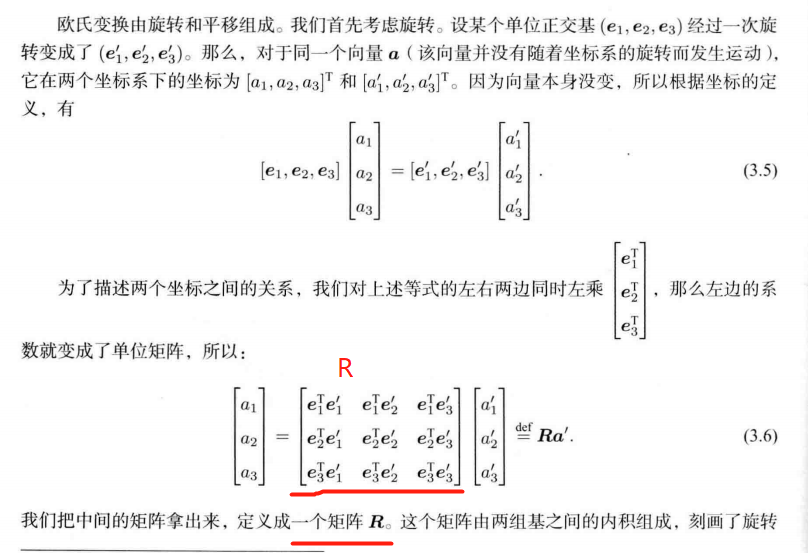


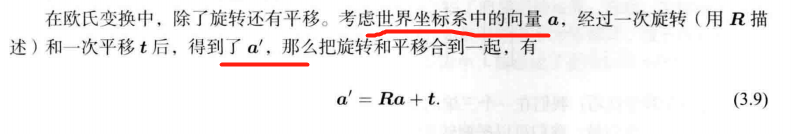
!!坐标系 转换
向量 a \bm{a} a 在坐标系1为 a 1 \bm{a_1} a1 , 在坐标系2 为 a 2 \bm{a_2} a2
a 1 = R 12 a 2 + t 12 \bm{a_1 = R_{12}a_2 + t_{12}} a1=R12a2+t12
R 12 \bm{R_{12}} R12 : 把坐标系2 的向量 变换到 坐标系1中【坐标系2中 坐标相对于 坐标系 1】
t 12 \bm{t_{12}} t12 : 坐标系1原点 指向 坐标系2原点 的向量。
我的坐标: 从世界坐标系 指向自己坐标系原点的向量

T
12
\bm{T_{12}}
T12: 2 相对于 1 的变换
Eigen: 纯用头文件搭建的库 【Code】
初始化:
#include<iostream>
#include<ctime>
#include<eigen3/Eigen/Core>
using namespace Eigen;
using namespace std;
int main(){
// 声明一个 2*3 的 float 矩阵
Matrix<float, 2, 3> matrix_23;
// 三维向量 Matrix<double, 3, 1>
Vector3d v_3d;
Matrix<float, 3, 1> vd_3d; // 等效
// 初始化 3阶 矩阵 为 0
Matrix3d matrix_33 = Matrix3d::Zero();
// 不确定 矩阵大小 , 动态定义 运行较慢
Matrix <double, Dynamic, Dynamic> matrix_dynamic;
MatrixXd matrix_x; // 等效
// 输入数据初始化
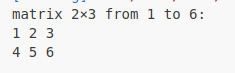
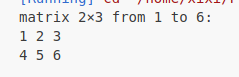
matrix_23 << 1, 2, 3, 4, 5, 6;
// 输出
cout << "matrix 2×3 from 1 to 6:\n" << matrix_23 << endl;
}
#include<iostream>
#include<ctime>
#include<eigen3/Eigen/Core>
using namespace Eigen;
using namespace std;
int main(){
// 声明一个 2*3 的 float 矩阵
Matrix<float, 2, 3> matrix_23;
// 输入数据初始化
matrix_23 << 1, 2, 3, 4, 5, 6;
/* 访问 矩阵中元素*/
cout << "print matrix 2×3:" << endl;
for (int i = 0; i < 2; i++){
for (int j = 0; j < 3; j++){
cout << matrix_23(i, j) << "\t";
}
cout << endl;
}
}
#include<iostream>
#include<ctime>
#include<eigen3/Eigen/Core>
using namespace Eigen;
using namespace std;
int main(){
// 声明一个 2*3 的 float 矩阵
Matrix<float, 2, 3> matrix_23;
// 输入数据初始化
matrix_23 << 1, 2, 3, 4, 5, 6;
Vector3d v_3d;
Matrix<float, 3, 1> vd_3d; // 注意 向量为 列
v_3d << 3, 2, 1;
vd_3d << 4, 5, 6;
/* 矩阵 和 向量 相乘*/
Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d; //类型不一致,需要显式强制变换
cout << "[1, 2, 3; 4, 5, 6] * [3, 2, 1] = " << result.transpose() << endl;
Matrix<float, 2, 1> result2 = matrix_23 * vd_3d; // 同类型
cout << "[1, 2, 3;4, 5, 6] * [4, 5, 6] = " << result2.transpose() << endl;
}

#include<iostream>
#include<ctime>
//#include<eigen3/Eigen/Core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
int main(int argc, char **argv){
/* 矩阵 基础运算 */
Matrix3d matrix_33 = Matrix3d::Random(); // 随机数 矩阵 随机的话 逆可能不存在
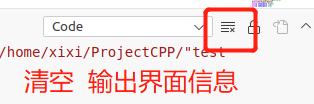
cout << "random matrix: \n" << matrix_33 << endl;
cout << "transpose: \n" << matrix_33.transpose() << endl; //转置
cout << "sum: " << matrix_33.sum() << endl;
cout << "trace: " << matrix_33.trace() << endl; // 迹:对角线元素之和
cout << "timme 10: \n" << 10 * matrix_33 << endl;
cout << "inverse: \n" << matrix_33.inverse() << endl; // 逆矩阵
cout << "det: " << matrix_33.determinant() << endl; // 行列式
return 0;
}
#include<iostream>
#include<ctime>
//#include<eigen3/Eigen/Core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
#define MATRIX_SIZE 50
int main(int argc, char **argv){
/* 矩阵 求特征值 */
// 实对称矩阵 可以保证对角化成功
Matrix3d matrix_33 = Matrix3d::Random();
SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33);
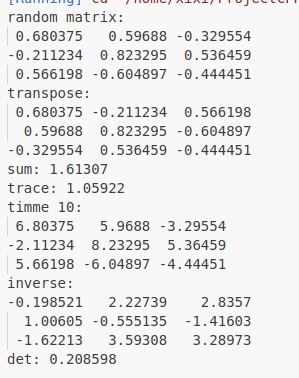
cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;
// 解方程 matrix_NN * x = V_Nd
/* 方法一: 求逆 计算量大*/
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN
= MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证 半正定
Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);
clock_t time_stt = clock(); // 计时
// 直接求逆
Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;
cout <<"time of normal inverse is "
<< 1000 * (clock() - time_stt)/(double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
/* 方法二: 矩阵分解 QR分解(将待求矩阵 分解为一个正交矩阵Q和一个上三角矩阵R) 速度 快些*/
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout << "time of Qr decomposition is "
<< 1000 * (clock() - time_stt)/(double) CLOCKS_PER_SEC <<"ms" << endl;
cout <<" x = " << x.transpose() << endl;
// 对于 正定矩阵, 还可以用 cholesky 分解来 解方程
time_stt = clock();
x = matrix_NN.ldlt().solve(v_Nd);
cout << "time of ldlt decomposition is "
<< 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;
cout << "x = " << x.transpose() << endl;
return 0;
}


3.3 旋转向量 和 欧拉角
旋转矩阵表示 的不足:
1、冗余
- 旋转矩阵:9个量 表示 3个自由度,
- 变换矩阵: 16个量 表达 6个自由度
2、需要满足约束条件:必须是正交矩阵,且行列式为1
旋转向量(Axis-Angle): 方向与旋转轴一致,长度等于旋转角
表示旋转的 2 种方式:
方式1: 旋转矩阵 R \bm{R} R
方式2: 向量 θ n \theta\bm{n} θn, 旋转轴为一个单位长度的向量 n \bm{n} n, 角度为 θ \theta θ
两者之间的转换关系:
1、 θ n \theta\bm{n} θn ——> R \bm{R} R
- 通过罗德里格斯公式(Rodrigues’s Formula)推导
R = c o s θ I + ( 1 − c o s θ ) n n T + s i n θ n ˆ \bm{R} = cos\theta\bm{I} + (1-cos\theta)\bm{n}\bm{n}^T + sin\theta\bm{n}\^{} R=cosθI+(1−cosθ)nnT+sinθnˆ2、 R \bm{R} R ——> θ n \theta\bm{n} θn
推导: 上述转换公式两边取 迹【矩阵的对角线元素之和;单位向量的迹为1】
- 反对称矩阵的主对角线元素必是零,所以其迹数为零
t r ( R ) = c o s θ ⋅ t r ( I ) + ( 1 − c o s θ ) ⋅ t r ( n n T ) + s i n θ ⋅ t r ( n ˆ ) = 3 c o s θ + ( 1 − c o s θ ) = 1 + 2 c o s θ \begin{align*} tr(\bm{R}) & = cos\theta ·tr({\bm{I}}) + (1-cos\theta) ·tr({\bm{n}\bm{n}^T}) + sin\theta · tr({\bm{n}\^{}} )\\ &= 3cos\theta + (1-cos\theta) \\ & = 1 + 2cos\theta \end{align*} tr(R)=cosθ⋅tr(I)+(1−cosθ)⋅tr(nnT)+sinθ⋅tr(nˆ)=3cosθ+(1−cosθ)=1+2cosθ
θ = a c o c o s t r ( R ) − 1 2 \theta = acocos\frac{tr(\bm{R})-1}{2} θ=acocos2tr(R)−1
旋转轴上的向量在旋转后不发生改变, 即
R n = n \bm{Rn = n} Rn=n
转轴 n \bm{n} n = 矩阵 R \bm{R} R 的特征值 1 对应的特征向量。
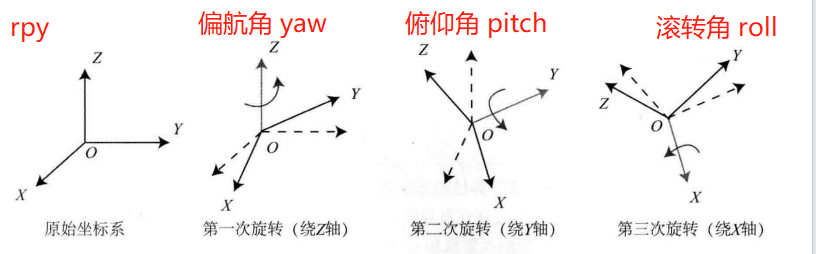
3.3.2 欧拉角 (一个旋转 分解成 3次 绕不同轴的旋转)
偏航-俯仰-滚转(yaw-pitch-roll) ZYX
一个三维向量 描述 任意旋转: [ r , p , y ] T [r, p, y]^T [r,p,y]T
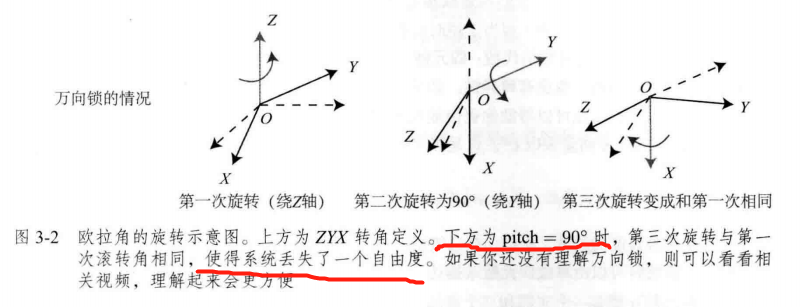
欧拉角 缺点: 万向锁问题 (Gimbal Lock)
在俯仰角为 ± 90° 时, 第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由 3 次旋转变成了 2 次 旋转) 奇异性问题
——————————————————————
欧拉角 不适用于:
1、插值 和 迭代
2、滤波 和 优化
适用于: 人机交互。
2D 运动的场合(扫地机、自动驾驶) 可将旋转 分解成 三个 欧拉角, 把其中一个 作为 定位信息。
——————————————————————
旋转向量的奇异性: 转角 θ \theta θ 超过 2 π 2\pi 2π 产生周期性时。
3.4 四元数(Quaternion)
1、旋转矩阵: 9个量 描述 3 自由度 冗余
2、欧拉角 和 旋转向量: 奇异性
- 用两个坐标表示地球表面(如经度 和 纬度) 存在奇异性 (纬度为 ± 90°时 经度 无意义)
3、四元数 紧凑且 没有奇异性 不够直观、运算稍复杂

——————————————
四元数的运算
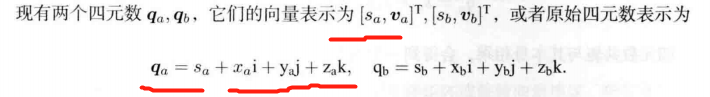
四元数乘法 不可交换




四元数 表示旋转
空间三维点: p = [ x , y , z ] \bm{p}=[x, y, z] p=[x,y,z]
一个由单位四元数 q \bm{q} q 指定的 旋转
三维点 p \bm{p} p 经旋转之后 变成了 p ′ \bm{p}^{\prime} p′
矩阵描述: p ′ = R p \bm{p}^{\prime} = \bm{Rp} p′=Rp
————————
四元数表示:
1、三维空间点 用一个 虚四元数 来描述:
- 相当于将 四元数的3个虚部 与 空间的3个轴 相对应。
p = [ 0 , x , y , z ] T = [ 0 , v ] T \bm{p} = [0, x, y, z]^T = [0, \bm{v}]^T p=[0,x,y,z]T=[0,v]T
2、旋转后
p ′ = q p q − 1 \bm{p}^{\prime} = \bm{qpq^{-1}} p′=qpq−1
可证明 结果 p ′ \bm{p}^{\prime} p′ 的实部为0, 虚部即为旋转之后的坐标。
3.4.4 四元数 到 其他旋转表示 的转换
四元数 ——> 旋转矩阵

推导过程
四元数 ——> 旋转向量

推导过程
——————
其它 会变形变换
从真实世界 到 相机照片 的变换是一个射影变换, 如果相机的焦距为无穷远,那么这个变换为仿射变换。
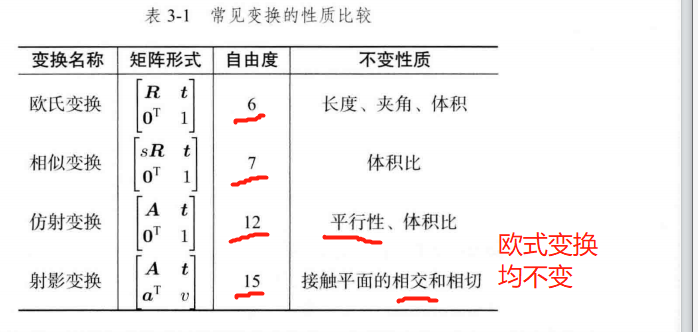
4、射影变换:近大远小 不规则的四边形
a
T
\bm{a}^T
aT 为缩放
2D 的射影变换 一共有8 个自由度, 3D有 15个自由度。
3、仿射变换 要求A为可逆,不必是正交【欧式变换要求是正交】。 正交投影 平行四边形
2、相似变换 面积改变
实践_ Eigen 几何模块 【Code】

#include<iostream>
#include<cmath>
//#include<eigen3/Eigen/Core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
#define MATRIX_SIZE 50
int main(int argc, char **argv){
// 3D 旋转矩阵 还有 Matrix3f
Matrix3d rotation_matrix = Matrix3d::Identity();
/* 旋转向量 */
AngleAxisd rotation_vector(M_PI/4, Vector3d(0, 0, 1)); // 沿Z轴旋转 45°
cout.precision(3);
cout << "rotation matrix = \n" << rotation_vector.matrix() << endl;
/* 旋转向量 转 旋转矩阵 */
rotation_matrix = rotation_vector.toRotationMatrix();
/* 坐标变换 */
// 用 AngleAxis【旋转向量】 进行坐标变换
Vector3d v(1, 0, 0);
Vector3d v_rotated = rotation_vector * v;
cout << "(1, 0, 0) after rotation (by angle axis) = " << v_rotated.transpose() << endl;
// 用旋转矩阵
v_rotated = rotation_matrix * v;
cout <<"(1, 0, 0) after rotation (by matrix ) = " << v_rotated.transpose() << endl;
/* 旋转矩阵 转 欧拉角 */
Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0) ; //ZYX 顺序
cout << "yaw pitch roll = " << euler_angles.transpose() << endl;
/* 欧式变换矩阵*/
Isometry3d T = Isometry3d::Identity(); // 4 * 4 矩阵
T.rotate(rotation_vector); // 按照 旋转向量 进行旋转
T.pretranslate(Vector3d(1, 3, 4)); // 平移向量 为 (1, 3, 4)
cout << "Transform matrix = \n" << T.matrix() << endl;
// 用变换矩阵进行 坐标变换
Vector3d v_transformed = T * v;
cout << "v transformed = " << v_transformed.transpose() << endl;
/* 四元数 */
// 将 旋转向量AngleAxis 赋值给 四元数
Quaterniond q = Quaterniond(rotation_vector) ;
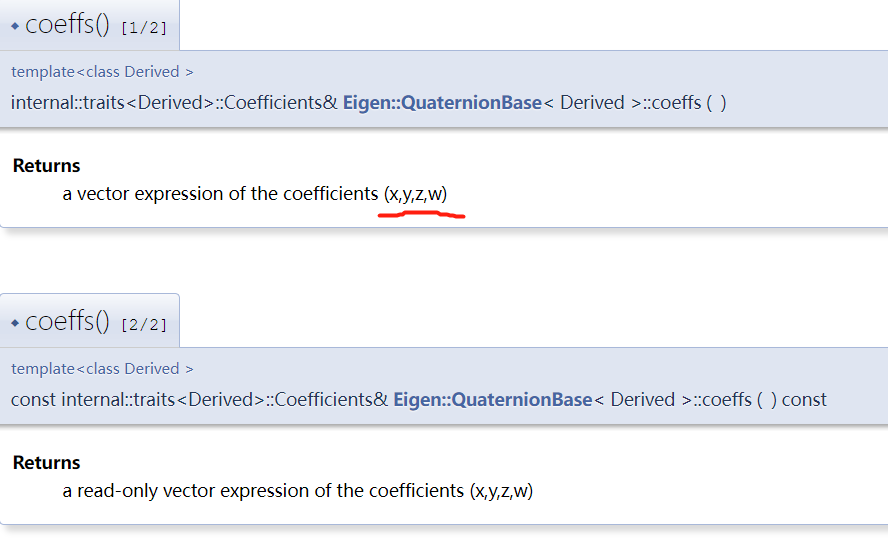
cout << "quaternion from rotation vector = " << q.coeffs().transpose() << endl;
// 把 旋转矩阵 赋给 四元数 .coeffs() 返回 向量[x, y, z, w]^T
q = Quaterniond(rotation_matrix);
cout << "quaterniond from rotation matrix = " << q.coeffs().transpose() << endl;
// 使用 四元数 旋转 一个向量
v_rotated = q * v; // 这里 重载了乘法, 和 数学描述 qpq^(-1) 不太一样
cout << "(1, 0, 0) after rotation = " << v_rotated.transpose() << endl;
// 使用常规 向量乘法
cout << "should be equal to " << (q * Quaterniond(0, 1, 0, 0) * q.inverse()).coeffs().transpose() << endl;
return 0;
}
Eigen 官方文档
链接:Eigen 官方文档
函数: coeffs()
坐标变换 举例:

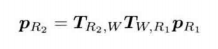
#include<iostream>
#include<ctime>
//#include<eigen3/Eigen/Core>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
#define MATRIX_SIZE 50
int main(int argc, char **argv){
Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2);
q1.normalize();
q2.normalize();
Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3); // 平移向量
Vector3d p1(0.5, 0, 0.2);
Isometry3d T1w(q1), T2w(q2); // 欧式旋转
T1w.pretranslate(t1); // 左乘 translate 右乘
T2w.pretranslate(t2);
Vector3d p2 = T2w * T1w.inverse() * p1;
cout << endl << p2.transpose() << endl;
return 0;
}

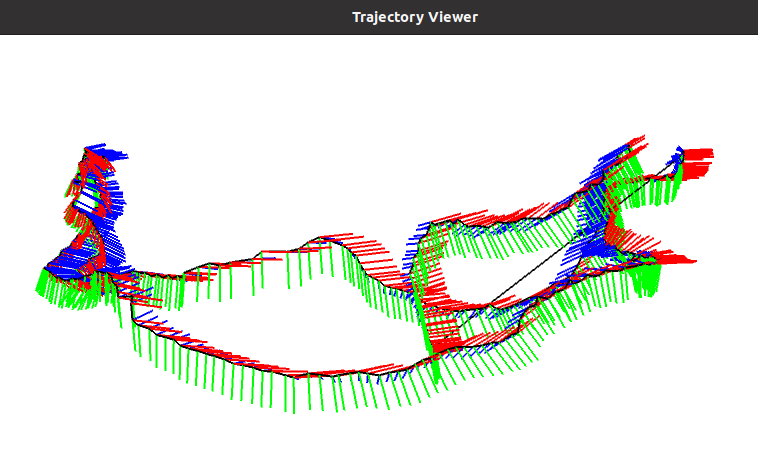
3.7.1 运动轨迹 显示 【Code】
源码 下成 第一版的了 。。。。

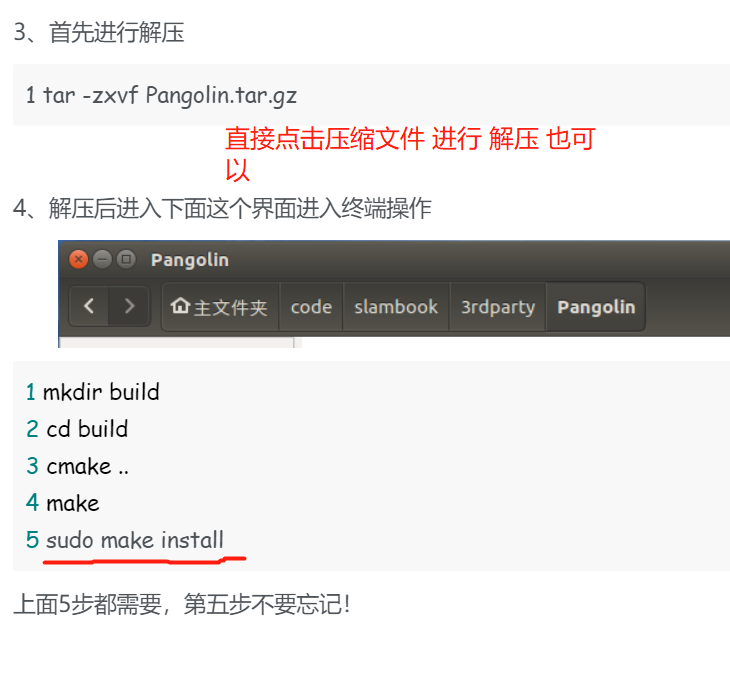
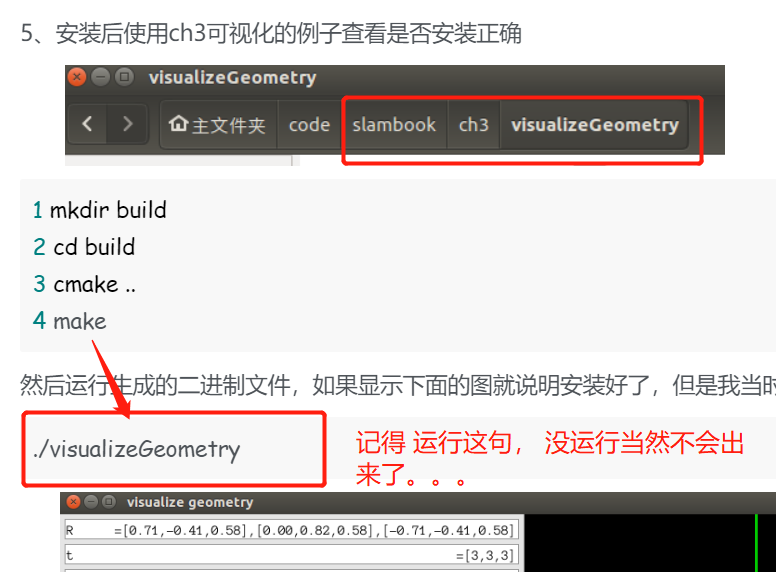
pangolin安装
注释
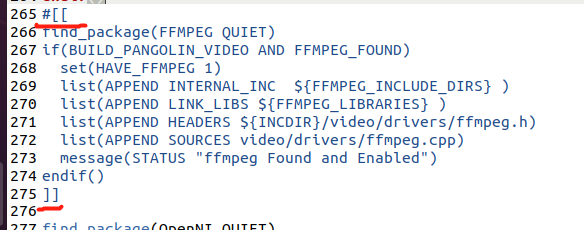
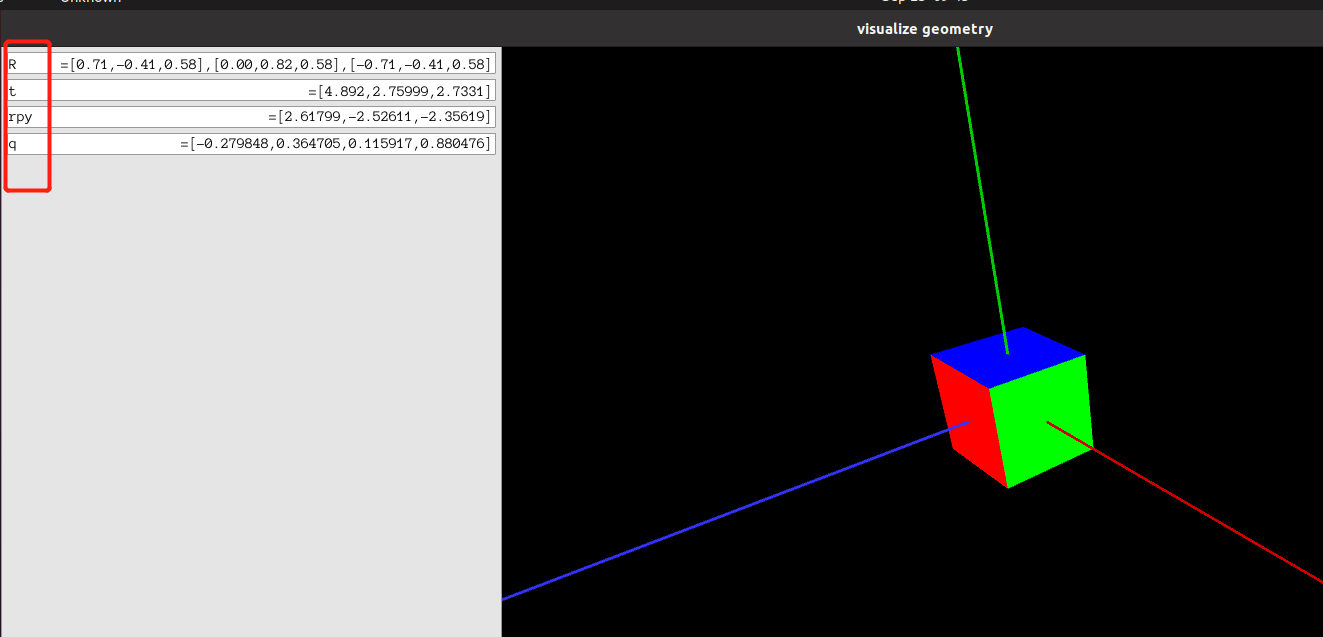
上述 显示相机位姿的.cpp 文件
#include <iostream>
#include <iomanip>
using namespace std;
#include <Eigen/Core>
#include <Eigen/Geometry>
using namespace Eigen;
#include <pangolin/pangolin.h>
struct RotationMatrix {
Matrix3d matrix = Matrix3d::Identity();
};
ostream &operator<<(ostream &out, const RotationMatrix &r) {
out.setf(ios::fixed);
Matrix3d matrix = r.matrix;
out << '=';
out << "[" << setprecision(2) << matrix(0, 0) << "," << matrix(0, 1) << "," << matrix(0, 2) << "],"
<< "[" << matrix(1, 0) << "," << matrix(1, 1) << "," << matrix(1, 2) << "],"
<< "[" << matrix(2, 0) << "," << matrix(2, 1) << "," << matrix(2, 2) << "]";
return out;
}
istream &operator>>(istream &in, RotationMatrix &r) {
return in;
}
struct TranslationVector {
Vector3d trans = Vector3d(0, 0, 0);
};
ostream &operator<<(ostream &out, const TranslationVector &t) {
out << "=[" << t.trans(0) << ',' << t.trans(1) << ',' << t.trans(2) << "]";
return out;
}
istream &operator>>(istream &in, TranslationVector &t) {
return in;
}
struct QuaternionDraw {
Quaterniond q;
};
ostream &operator<<(ostream &out, const QuaternionDraw quat) {
auto c = quat.q.coeffs();
out << "=[" << c[0] << "," << c[1] << "," << c[2] << "," << c[3] << "]";
return out;
}
istream &operator>>(istream &in, const QuaternionDraw quat) {
return in;
}
int main(int argc, char **argv) {
pangolin::CreateWindowAndBind("visualize geometry", 1000, 600);
glEnable(GL_DEPTH_TEST);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1000, 600, 420, 420, 500, 300, 0.1, 1000),
pangolin::ModelViewLookAt(3, 3, 3, 0, 0, 0, pangolin::AxisY)
);
const int UI_WIDTH = 500;
pangolin::View &d_cam = pangolin::CreateDisplay().
SetBounds(0.0, 1.0, pangolin::Attach::Pix(UI_WIDTH), 1.0, -1000.0f / 600.0f).
SetHandler(new pangolin::Handler3D(s_cam));
// ui
pangolin::Var<RotationMatrix> rotation_matrix("ui.R", RotationMatrix());
pangolin::Var<TranslationVector> translation_vector("ui.t", TranslationVector());
pangolin::Var<TranslationVector> euler_angles("ui.rpy", TranslationVector());
pangolin::Var<QuaternionDraw> quaternion("ui.q", QuaternionDraw());
pangolin::CreatePanel("ui").SetBounds(0.0, 1.0, 0.0, pangolin::Attach::Pix(UI_WIDTH));
while (!pangolin::ShouldQuit()) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
pangolin::OpenGlMatrix matrix = s_cam.GetModelViewMatrix();
Matrix<double, 4, 4> m = matrix;
RotationMatrix R;
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
R.matrix(i, j) = m(j, i);
rotation_matrix = R;
TranslationVector t;
t.trans = Vector3d(m(0, 3), m(1, 3), m(2, 3));
t.trans = -R.matrix * t.trans;
translation_vector = t;
TranslationVector euler;
euler.trans = R.matrix.eulerAngles(2, 1, 0);
euler_angles = euler;
QuaternionDraw quat;
quat.q = Quaterniond(R.matrix);
quaternion = quat;
glColor3f(1.0, 1.0, 1.0);
pangolin::glDrawColouredCube();
// draw the original axis
glLineWidth(3);
glColor3f(0.8f, 0.f, 0.f);
glBegin(GL_LINES);
glVertex3f(0, 0, 0);
glVertex3f(10, 0, 0);
glColor3f(0.f, 0.8f, 0.f);
glVertex3f(0, 0, 0);
glVertex3f(0, 10, 0);
glColor3f(0.2f, 0.2f, 1.f);
glVertex3f(0, 0, 0);
glVertex3f(0, 0, 10);
glEnd();
pangolin::FinishFrame();
}
}
CMakeLists.txt
cmake_minimum_required( VERSION 2.8 )
project( visualizeGeometry )
set(CMAKE_CXX_FLAGS "-std=c++11")
# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )
# 添加Pangolin依赖
find_package( Pangolin )
include_directories( ${Pangolin_INCLUDE_DIRS} )
add_executable( visualizeGeometry visualizeGeometry.cpp )
target_link_libraries( visualizeGeometry ${Pangolin_LIBRARIES} )
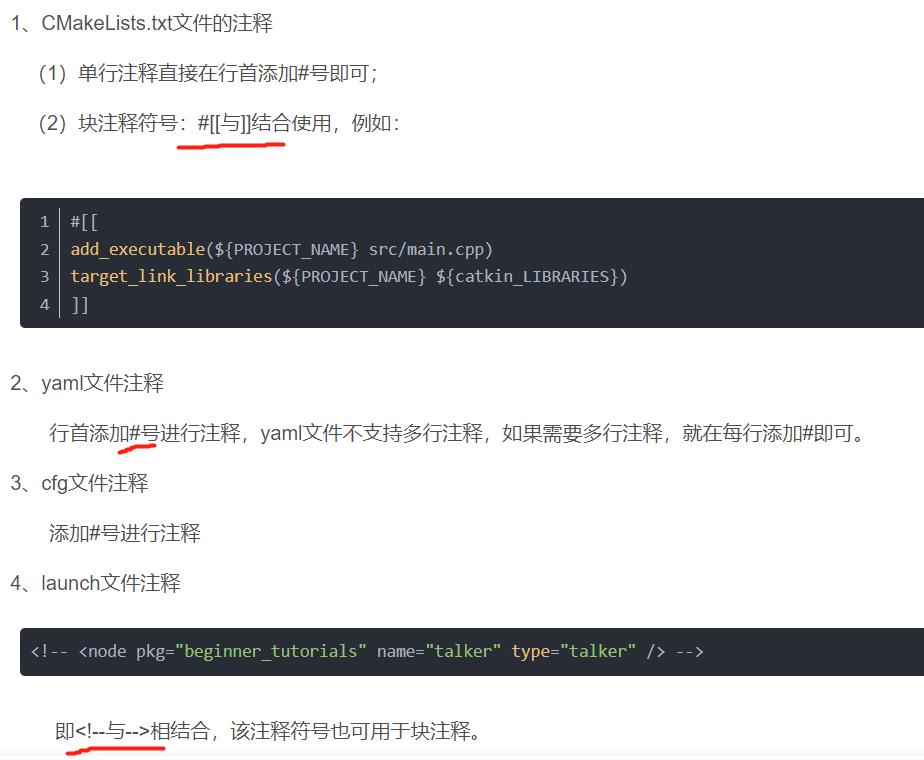
!!!一些文件的注释语法
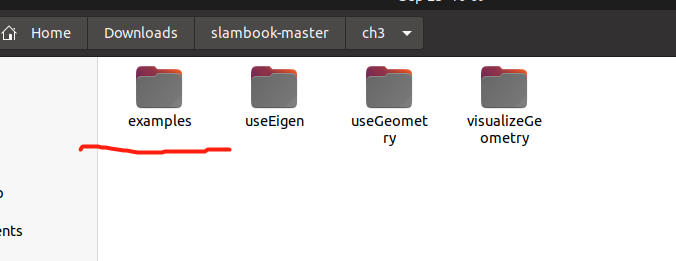
———————— 只是下错 版本了,下成版本1的源码了
问题: 在文件里 没找到example 文件夹
下载特定文件夹网址: http://kinolien.github.io/gitzip/
粘贴该地址: https://github.com/gaoxiang12/slambook2/tree/master/ch3/examples
补上了
——————————
#include <pangolin/pangolin.h>
#include <Eigen/Core>
#include <unistd.h>
// 本例演示了如何画出一个预先存储的轨迹
using namespace std;
using namespace Eigen;
// path to trajectory file
string trajectory_file = "./examples/trajectory.txt";
void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>>);
int main(int argc, char **argv) {
vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses;
ifstream fin(trajectory_file);
if (!fin) {
cout << "cannot find trajectory file at " << trajectory_file << endl;
return 1;
}
while (!fin.eof()) {
double time, tx, ty, tz, qx, qy, qz, qw;
fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
Isometry3d Twr(Quaterniond(qw, qx, qy, qz));
Twr.pretranslate(Vector3d(tx, ty, tz));
poses.push_back(Twr);
}
cout << "read total " << poses.size() << " pose entries" << endl;
// draw trajectory in pangolin
DrawTrajectory(poses);
return 0;
}
/*******************************************************************************************/
void DrawTrajectory(vector<Isometry3d, Eigen::aligned_allocator<Isometry3d>> poses) {
// create pangolin window and plot the trajectory
pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);
glEnable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
pangolin::OpenGlRenderState s_cam(
pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
);
pangolin::View &d_cam = pangolin::CreateDisplay()
.SetBounds(0.0, 1.0, 0.0, 1.0, -1024.0f / 768.0f)
.SetHandler(new pangolin::Handler3D(s_cam));
while (pangolin::ShouldQuit() == false) {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
d_cam.Activate(s_cam);
glClearColor(1.0f, 1.0f, 1.0f, 1.0f);
glLineWidth(2);
for (size_t i = 0; i < poses.size(); i++) {
// 画每个位姿的三个坐标轴
Vector3d Ow = poses[i].translation();
Vector3d Xw = poses[i] * (0.1 * Vector3d(1, 0, 0));
Vector3d Yw = poses[i] * (0.1 * Vector3d(0, 1, 0));
Vector3d Zw = poses[i] * (0.1 * Vector3d(0, 0, 1));
glBegin(GL_LINES);
glColor3f(1.0, 0.0, 0.0);
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Xw[0], Xw[1], Xw[2]);
glColor3f(0.0, 1.0, 0.0);
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Yw[0], Yw[1], Yw[2]);
glColor3f(0.0, 0.0, 1.0);
glVertex3d(Ow[0], Ow[1], Ow[2]);
glVertex3d(Zw[0], Zw[1], Zw[2]);
glEnd();
}
// 画出连线
for (size_t i = 0; i < poses.size(); i++) {
glColor3f(0.0, 0.0, 0.0);
glBegin(GL_LINES);
auto p1 = poses[i], p2 = poses[i + 1];
glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
glEnd();
}
pangolin::FinishFrame();
usleep(5000); // sleep 5 ms
}
}
1、将路径改为 绝对路径
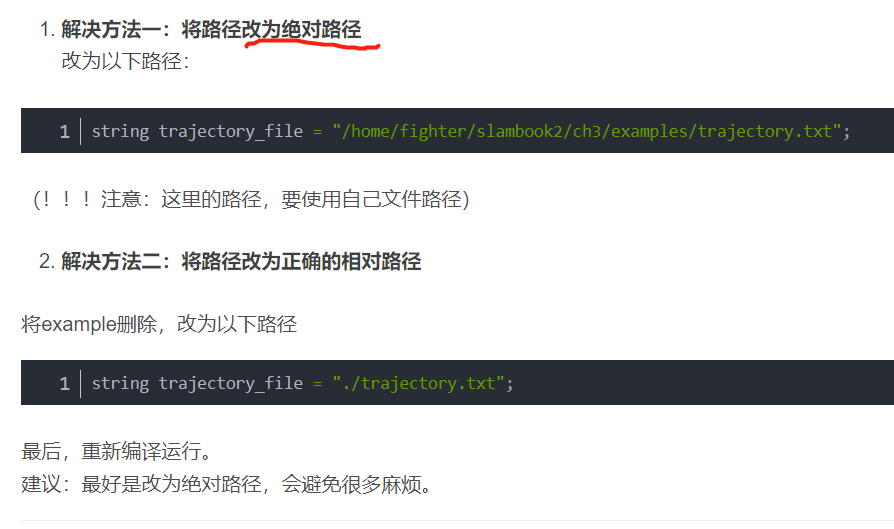
输出绝对路径 命令
pwd

mkdir build && cd build # 要是已经建过 build ,直接 cd build
cmake ..
make
./plotTrajectory

CMakeLists.txt
include_directories("/usr/include/eigen3")
add_executable(coordinateTransform coordinateTransform.cpp)
find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})
add_executable(plotTrajectory plotTrajectory.cpp)
target_link_libraries(plotTrajectory ${Pangolin_LIBRARIES})
习题

P8
1、
2、高斯分布
也称为 正态分布
p ( x ; μ , σ 2 ) = 1 2 π σ e x p ( − ( x − μ ) 2 2 σ 2 ) p(x; μ, σ^2)=\frac{1}{\sqrt{2π}σ}exp(-\frac{(x-μ)^2}{2σ^2}) p(x;μ,σ2)=2πσ1exp(−2σ2(x−μ)2)

3、
STL:
STL(Standard Template Library,标准模板库)是惠普实验室开发的一系列软件的统称。
STL的代码从广义上讲分为三类:algorithm(算法)、container(容器)和iterator(迭代器)
在C++标准中,STL被组织为下面的13个头文件:<algorithm>、<deque>、<functional>、<iterator>、<vector>、<list>、<map>、<memory>、<numeric>、<queue>、<set>、<stack>和<utility>。
5、C++标准
ls --help
cat --help
7、Linux的目录结构
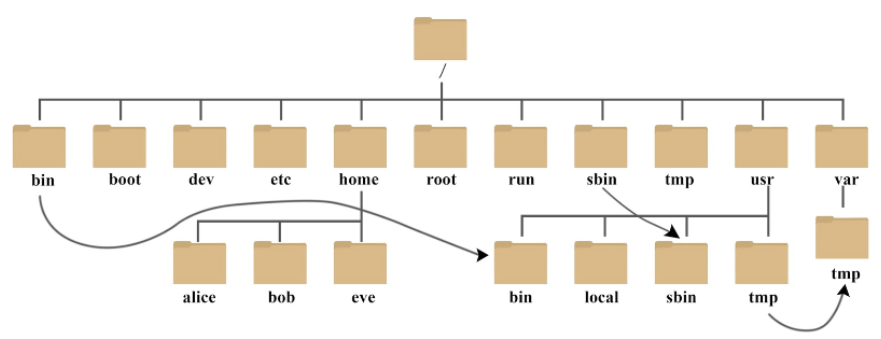

8、Ubuntu 安装软件
在Ubuntu 16 之前要使用apt-get install 软件包来安装,在Ubuntu 16 之后可以直接使用apt install 软件包来安装。这种方法安装的包有时候不好用,比如VSCode 会无法使用中文输入。

sudo dpkg -i 文件名.deb
5)、CMake 方法,包里包含 CMakeLists.txt文件
mkdir build && cd build
cmake ..
make
sudo make install

两种写法均可 在g++后添加 -o 输出文件名
g++ -o helloSLAM.exe helloSLAM.cpp
g++ helloSLAM.cpp -o helloSLAM.out

习题_第 3 讲 三维空间刚体运动

√ 题1
1、验证旋转矩阵 是 正交矩阵。
正交矩阵满足
A
A
T
=
I
\bm{AA^T} = I
AAT=I, 即只要满足
A
−
1
=
A
T
\bm{A^{-1}} = \bm{A^T}
A−1=AT, 则
A
\bm{A}
A 是正交矩阵。
根据 P44 页的定义:
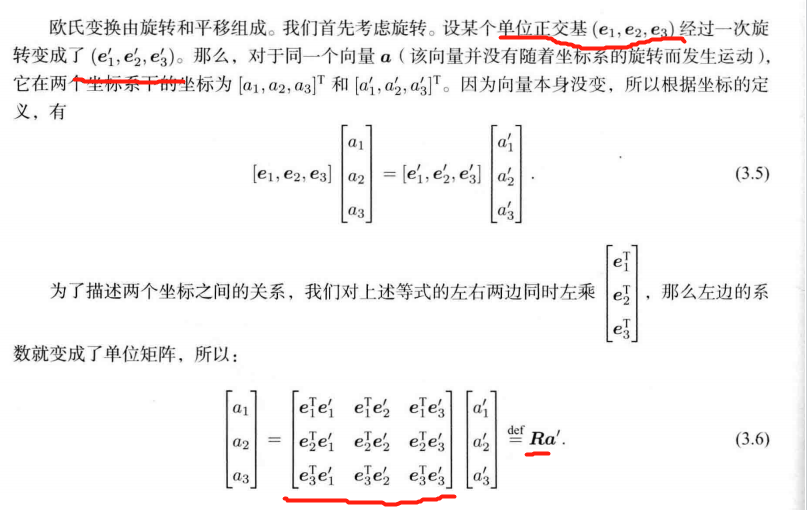
R = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] \bm{R} = \begin{bmatrix} \bm{e}_1^T\bm{e}_1^{\prime} & \bm{e}_1^T\bm{e}_2^{\prime} & \bm{e}_1^T\bm{e}_3^{\prime} \\ \bm{e}_2^T\bm{e}_1^{\prime} & \bm{e}_2^T\bm{e}_2^{\prime} & \bm{e}_2^T\bm{e}_3^{\prime} \\ \bm{e}_3^T\bm{e}_1^{\prime} & \bm{e}_3^T\bm{e}_2^{\prime} & \bm{e}_3^T\bm{e}_3^{\prime} \end{bmatrix} R= e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′
R T = [ e 1 T e 1 ′ e 1 T e 2 ′ e 1 T e 3 ′ e 2 T e 1 ′ e 2 T e 2 ′ e 2 T e 3 ′ e 3 T e 1 ′ e 3 T e 2 ′ e 3 T e 3 ′ ] T = [ e 1 ′ T e 1 e 2 ′ T e 1 e 3 ′ T e 1 e 1 ′ T e 2 e 2 ′ T e 2 e 3 ′ T e 2 e 1 ′ T e 3 e 2 ′ T e 3 e 3 ′ T e 3 ] \bm{R^T} = \begin{bmatrix} \bm{e}_1^T\bm{e}_1^{\prime} & \bm{e}_1^T\bm{e}_2^{\prime} & \bm{e}_1^T\bm{e}_3^{\prime} \\ \bm{e}_2^T\bm{e}_1^{\prime} & \bm{e}_2^T\bm{e}_2^{\prime} & \bm{e}_2^T\bm{e}_3^{\prime} \\ \bm{e}_3^T\bm{e}_1^{\prime} & \bm{e}_3^T\bm{e}_2^{\prime} & \bm{e}_3^T\bm{e}_3^{\prime} \end{bmatrix}^T = \begin{bmatrix} {\bm{e}_1^{\prime}}^T\bm{e}_1& {\bm{e}_2^{\prime}}^T\bm{e}_1 & {\bm{e}_3^{\prime}}^T\bm{e}_1 \\ {\bm{e}_1^{\prime}}^T\bm{e}_2& {\bm{e}_2^{\prime}}^T\bm{e}_2 & {\bm{e}_3^{\prime}}^T\bm{e}_2 \\ {\bm{e}_1^{\prime}}^T\bm{e}_3& {\bm{e}_2^{\prime}}^T\bm{e}_3 & {\bm{e}_3^{\prime}}^T\bm{e}_3 \end{bmatrix} RT= e1Te1′e2Te1′e3Te1′e1Te2′e2Te2′e3Te2′e1Te3′e2Te3′e3Te3′ T= e1′Te1e1′Te2e1′Te3e2′Te1e2′Te2e2′Te3e3′Te1e3′Te2e3′Te3
对于 式(3.5), 同时左乘 [ e 1 ′ , e 2 ′ , e 3 ′ ] T [\bm{e}_1^{\prime} , \bm{e}_2^{\prime} , \bm{e}_3^{\prime} ]^T [e1′,e2′,e3′]T
[ e 1 ′ , e 2 ′ , e 3 ′ ] T [ e 1 , e 2 , e 3 ] [ a 1 a 2 a 3 ] = [ e 1 ′ , e 2 ′ , e 3 ′ ] T [ e 1 ′ , e 2 ′ , e 3 ′ ] [ a 1 ′ a 2 ′ a 3 ′ ] [\bm{e}_1^{\prime} , \bm{e}_2^{\prime} , \bm{e}_3^{\prime} ]^T[\bm{e}_1, \bm{e}_2, \bm{e}_3] \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}= [\bm{e}_1^{\prime} , \bm{e}_2^{\prime} , \bm{e}_3^{\prime} ]^T[\bm{e}_1^{\prime} , \bm{e}_2^{\prime} , \bm{e}_3^{\prime}]\begin{bmatrix} a_1^{\prime} \\ a_2^{\prime} \\ a_3^{\prime} \end{bmatrix} [e1′,e2′,e3′]T[e1,e2,e3] a1a2a3 =[e1′,e2′,e3′]T[e1′,e2′,e3′] a1′a2′a3′
等式右边 由于
[
e
1
′
,
e
2
′
,
e
3
′
]
[\bm{e}_1^{\prime} , \bm{e}_2^{\prime} , \bm{e}_3^{\prime} ]
[e1′,e2′,e3′] 为单位正交基,得到 单位矩阵,则:
[
e
1
′
T
e
1
e
2
′
T
e
1
e
3
′
T
e
1
e
1
′
T
e
2
e
2
′
T
e
2
e
3
′
T
e
2
e
1
′
T
e
3
e
2
′
T
e
3
e
3
′
T
e
3
]
[
a
1
a
2
a
3
]
=
[
a
1
′
a
2
′
a
3
′
]
\begin{bmatrix} {\bm{e}_1^{\prime}}^T\bm{e}_1& {\bm{e}_2^{\prime}}^T\bm{e}_1 & {\bm{e}_3^{\prime}}^T\bm{e}_1 \\ {\bm{e}_1^{\prime}}^T\bm{e}_2& {\bm{e}_2^{\prime}}^T\bm{e}_2 & {\bm{e}_3^{\prime}}^T\bm{e}_2 \\ {\bm{e}_1^{\prime}}^T\bm{e}_3& {\bm{e}_2^{\prime}}^T\bm{e}_3 & {\bm{e}_3^{\prime}}^T\bm{e}_3 \end{bmatrix}\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix}=\begin{bmatrix} a_1^{\prime} \\ a_2^{\prime} \\ a_3^{\prime} \end{bmatrix}
e1′Te1e1′Te2e1′Te3e2′Te1e2′Te2e2′Te3e3′Te1e3′Te2e3′Te3
a1a2a3
=
a1′a2′a3′
与 式 (3.6) 对比,可得
R
−
1
=
[
e
1
′
T
e
1
e
2
′
T
e
1
e
3
′
T
e
1
e
1
′
T
e
2
e
2
′
T
e
2
e
3
′
T
e
2
e
1
′
T
e
3
e
2
′
T
e
3
e
3
′
T
e
3
]
=
R
T
\bm{R^{-1}} = \begin{bmatrix} {\bm{e}_1^{\prime}}^T\bm{e}_1& {\bm{e}_2^{\prime}}^T\bm{e}_1 & {\bm{e}_3^{\prime}}^T\bm{e}_1 \\ {\bm{e}_1^{\prime}}^T\bm{e}_2& {\bm{e}_2^{\prime}}^T\bm{e}_2 & {\bm{e}_3^{\prime}}^T\bm{e}_2 \\ {\bm{e}_1^{\prime}}^T\bm{e}_3& {\bm{e}_2^{\prime}}^T\bm{e}_3 & {\bm{e}_3^{\prime}}^T\bm{e}_3 \end{bmatrix} = \bm{R^T}
R−1=
e1′Te1e1′Te2e1′Te3e2′Te1e2′Te2e2′Te3e3′Te1e3′Te2e3′Te3
=RT
证毕。
√ 题2
2、罗德里格斯公式推导
已知 旋转向量 为 θ n \theta\bm{n} θn, 求相应的旋转矩阵。
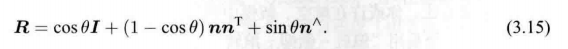
参考:维基百科证明链接
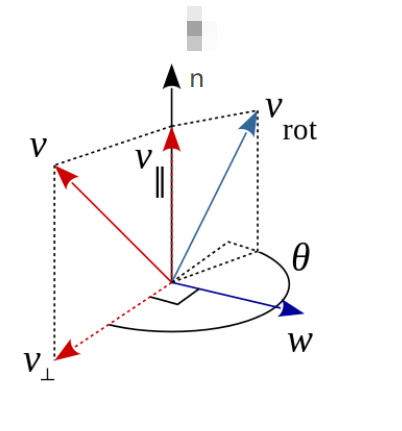
向量
v
\bm{v}
v 沿着单位旋转轴
n
\bm{n}
n 旋转
θ
\theta
θ 后得到向量
v
r
o
t
\bm{v}_{rot}
vrot
对于相应的旋转矩阵
R
\bm{R}
R,有
v
r
o
t
=
R
v
\bm{v}_{rot}=\bm{R}\bm{v}
vrot=Rv
——> 目标: 用
v
\bm{v}
v 表示
v
r
o
t
,
R
用
n
和
θ
\bm{v}_{rot},\bm{R} 用 \bm{n} 和 \theta
vrot,R用n和θ表示
将向量
v
\bm{v}
v 分解为平行于单位旋转轴
n
\bm{n}
n 的分量
v
∥
\bm{v}_{\parallel}
v∥和 平行于单位旋转轴
n
\bm{n}
n 法平面的分量
v
⊥
\bm{v}_{\perp}
v⊥
v
=
v
∥
+
v
⊥
\bm{v} = \bm{v}_{\parallel}+\bm{v}_{\perp}
v=v∥+v⊥
v
r
o
t
=
v
r
o
t
∥
+
v
r
o
t
⊥
\bm{v}_{rot} = \bm{v}_{{rot}\parallel} +\bm{v}_{{rot}\perp}
vrot=vrot∥+vrot⊥
其中 v r o t ∥ = v ∥ \bm{v}_{{rot}\parallel}=\bm{v}_{\parallel} vrot∥=v∥
现在找 v r o t ⊥ \bm{v}_{{rot}\perp} vrot⊥ 和 v ⊥ \bm{v}_{\perp} v⊥之间的关系。
- 同一平面,方便转换
注意 旋转向量的旋转角的定义,是
v
r
o
t
⊥
\bm{v}_{{rot}\perp}
vrot⊥ 和
v
⊥
\bm{v}_{\perp}
v⊥ 之间的角度, 本题图中
θ
\theta
θ 为钝角。旋转前后向量的模不变。
叉乘的右手定则: 右手四指沿着 叉乘的第一个向量朝第二个向量弯曲,与拇指朝向相同的为正。否则为负。
v r o t ⊥ = 平行于 v ⊥ 的分量 + 平行于 n × v ⊥ ( 即 w ) 的分量 = − c o s ( 180 − θ ) v ⊥ + s i n ( 180 − θ ) n × v ⊥ = c o s θ v ⊥ + s i n ( θ ) n × v ⊥ \begin{align*}\bm{v}_{{rot}\perp} &= 平行于 \bm{v}_{\perp}的分量 + 平行于 \bm{n}×\bm{v}_{\perp} (即\bm{w})的分量 \\ & = -cos(180-\theta)\bm{v}_{\perp} + sin(180-\theta) \bm{n}×\bm{v}_{\perp} \\ & = cos\theta\bm{v}_{\perp} + sin(\theta) \bm{n}× \bm{v}_{\perp} \end{align*} vrot⊥=平行于v⊥的分量+平行于n×v⊥(即w)的分量=−cos(180−θ)v⊥+sin(180−θ)n×v⊥=cosθv⊥+sin(θ)n×v⊥
则
v
r
o
t
=
v
r
o
t
∥
+
v
r
o
t
⊥
=
v
∥
+
c
o
s
θ
v
⊥
+
s
i
n
(
θ
)
n
×
v
⊥
=
v
∥
+
c
o
s
θ
(
v
−
v
∥
)
+
s
i
n
(
θ
)
n
×
v
⊥
=
c
o
s
θ
v
+
(
1
−
c
o
s
θ
)
v
∥
+
s
i
n
(
θ
)
n
×
v
⊥
想办法把其中的分量都转成
v
和
n
其中
v
∥
=
(
n
⋅
v
)
n
:
点乘得到投影的模再乘上向量方向
n
×
v
⊥
=
n
×
(
v
−
v
∥
)
=
n
×
v
。两平行向量叉乘结果为
0
。
原式
=
c
o
s
θ
v
+
(
1
−
c
o
s
θ
)
(
n
⋅
v
)
n
+
s
i
n
(
θ
)
n
×
v
=
(
c
o
s
θ
I
+
(
1
−
c
o
s
θ
)
n
n
+
s
i
n
(
θ
)
n
∧
)
v
=
(
c
o
s
θ
I
+
(
1
−
c
o
s
θ
)
n
n
T
+
s
i
n
(
θ
)
n
∧
)
v
即
R
=
c
o
s
θ
I
+
(
1
−
c
o
s
θ
)
n
n
T
+
s
i
n
(
θ
)
n
∧
注意
n
∧
等效于
n
×
\begin{align*}\bm{v}_{rot} & = \bm{v}_{{rot}\parallel} +\bm{v}_{{rot}\perp}\\ &=\bm{v}_{\parallel}+ cos\theta\bm{v}_{\perp} + sin(\theta) \bm{n}× \bm{v}_{\perp} \\ &=\bm{v}_{\parallel}+ cos\theta(\bm{v}-\bm{v}_{\parallel} )+ sin(\theta) \bm{n}× \bm{v}_{\perp} \\ &= cos\theta\bm{v}+(1-cos\theta)\bm{v}_{\parallel} + sin(\theta) \bm{n}× \bm{v}_{\perp} \\ & 想办法把其中的分量都转成 \bm{v} 和 \bm{n} \\ & 其中 \bm{v}_{\parallel} = (\bm{n}·\bm{v})\bm{n}: 点乘得到投影的模再乘上向量方向\\ &\bm{n}× \bm{v}_{\perp} = \bm{n}× (\bm{v} - \bm{v}_{\parallel}) = \bm{n}× \bm{v} 。两平行向量叉乘结果为0。\\ 原式 & = cos\theta\bm{v}+(1-cos\theta) (\bm{n}·\bm{v})\bm{n} + sin(\theta) \bm{n}× \bm{v} \\ & = (cos\theta\bm{I} +(1-cos\theta) \bm{n}\bm{n} + sin(\theta) \bm{n}^{\land} )\bm{v} \\ & = (cos\theta\bm{I} +(1-cos\theta) \bm{n}\bm{n}^T + sin(\theta) \bm{n}^{\land} )\bm{v} \\ 即 \bm{R} &= cos\theta\bm{I} +(1-cos\theta) \bm{n}\bm{n}^T + sin(\theta) \bm{n}^{\land} \\ & 注意 \bm{n}^{\land} 等效于 \bm{n}× \\ \end{align*}
vrot原式即R=vrot∥+vrot⊥=v∥+cosθv⊥+sin(θ)n×v⊥=v∥+cosθ(v−v∥)+sin(θ)n×v⊥=cosθv+(1−cosθ)v∥+sin(θ)n×v⊥想办法把其中的分量都转成v和n其中v∥=(n⋅v)n:点乘得到投影的模再乘上向量方向n×v⊥=n×(v−v∥)=n×v。两平行向量叉乘结果为0。=cosθv+(1−cosθ)(n⋅v)n+sin(θ)n×v=(cosθI+(1−cosθ)nn+sin(θ)n∧)v=(cosθI+(1−cosθ)nnT+sin(θ)n∧)v=cosθI+(1−cosθ)nnT+sin(θ)n∧注意n∧等效于n×
证毕。
LaTex:
$\bm{n}^{\land}$
n ∧ \bm{n}^{\land} n∧
√ 题3
3、验证四元数旋转某个点后,结果是一个虚四元数(实部为零),所以仍然对应到一个三维空间点。

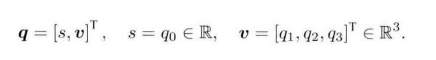
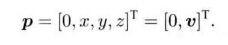


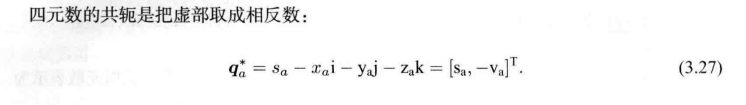
方法一: 直接点乘
p ′ = q p q − 1 = q p q ∗ / ∣ ∣ q ∣ ∣ 2 = ( q 0 + q 1 i + q 2 j + q 3 k ) ⋅ ( 0 + x i + y j + z k ) ⋅ ( q 0 − q 1 i − q 2 j − q 3 k ) q 0 2 + q 1 2 + q 2 2 + q 3 2 由于垂直向量点乘为 0 : 原式 = ( q 0 ⋅ ( x i + y j + z k ) + q 1 x + q 2 y + q 3 z ) ⋅ ( q 0 − q 1 i − q 2 j − q 3 k ) q 0 2 + q 1 2 + q 2 2 + q 3 2 = q 0 2 ⋅ ( x i + y j + z k ) + q 0 q 1 x + q 0 q 2 y + q 0 q 3 z q 0 2 + q 1 2 + q 2 2 + q 3 2 + − q 0 q 1 x − q 1 ( q 1 x + q 2 y + q 3 z ) i q 0 2 + q 1 2 + q 2 2 + q 3 2 + − q 0 q 2 y − q 2 ( q 1 x + q 2 y + q 3 z ) j q 0 2 + q 1 2 + q 2 2 + q 3 2 + − q 0 q 3 z − q 3 ( q 1 x + q 2 y + q 3 z ) k q 0 2 + q 1 2 + q 2 2 + q 3 2 虚四元数的实部为零,所以只需要重点关注实数部分求和是否为 0 即可: = q 0 2 x − q 1 ( q 1 x + q 2 y + q 3 z ) q 0 2 + q 1 2 + q 2 2 + q 3 2 i + q 0 2 y − q 2 ( q 1 x + q 2 y + q 3 z ) q 0 2 + q 1 2 + q 2 2 + q 3 2 j + q 0 2 z − q 3 ( q 1 x + q 2 y + q 3 z ) q 0 2 + q 1 2 + q 2 2 + q 3 2 k \begin{align*}\bm{p}^\prime &= \bm{qpq^{-1}} \\ &= \bm{qpq^*/||q||^2} \\ & = \frac{(q_0 + q_1\bm{i}+q_2\bm{j}+q_3\bm{k})·(0 + x\bm{i}+y\bm{j}+z\bm{k})·(q_0 - q_1\bm{i}-q_2\bm{j}-q_3\bm{k})}{q_0^2 +q_1^2 +q_2^2 +q_3^2 } \\ &由于垂直向量 点乘为0 :\\ 原式 & = \frac{(q_0·( x\bm{i}+y\bm{j}+z\bm{k})+ q_1x + q_2y +q_3z)·(q_0 - q_1\bm{i}-q_2\bm{j}-q_3\bm{k})}{q_0^2 +q_1^2 +q_2^2 +q_3^2 } \\ & = \frac{q_0^2·( x\bm{i}+y\bm{j}+z\bm{k})+ q_0q_1x + q_0q_2y +q_0q_3z }{q_0^2 +q_1^2 +q_2^2 +q_3^2 }\\ & +\frac{ - q_0q_1x-q_1( q_1x + q_2y +q_3z)\bm{i}}{q_0^2 +q_1^2 +q_2^2 +q_3^2 } \\ & +\frac{ - q_0q_2y-q_2( q_1x + q_2y +q_3z)\bm{j}}{q_0^2 +q_1^2 +q_2^2 +q_3^2 } \\ & +\frac{ - q_0q_3z-q_3( q_1x + q_2y +q_3z)\bm{k}}{q_0^2 +q_1^2 +q_2^2 +q_3^2 } \\ & 虚四元数的实部为零,所以只需要重点关注实数部分求和是否为0即可:\\ & = \frac{q_0^2x-q_1( q_1x + q_2y +q_3z)}{q_0^2 +q_1^2 +q_2^2 +q_3^2 }\bm{i}+ \frac{q_0^2y-q_2( q_1x + q_2y +q_3z)}{q_0^2 +q_1^2 +q_2^2 +q_3^2 }\bm{j}+\frac{q_0^2z-q_3( q_1x + q_2y +q_3z)}{q_0^2 +q_1^2 +q_2^2 +q_3^2 }\bm{k} \end{align*} p′原式=qpq−1=qpq∗/∣∣q∣∣2=q02+q12+q22+q32(q0+q1i+q2j+q3k)⋅(0+xi+yj+zk)⋅(q0−q1i−q2j−q3k)由于垂直向量点乘为0:=q02+q12+q22+q32(q0⋅(xi+yj+zk)+q1x+q2y+q3z)⋅(q0−q1i−q2j−q3k)=q02+q12+q22+q32q02⋅(xi+yj+zk)+q0q1x+q0q2y+q0q3z+q02+q12+q22+q32−q0q1x−q1(q1x+q2y+q3z)i+q02+q12+q22+q32−q0q2y−q2(q1x+q2y+q3z)j+q02+q12+q22+q32−q0q3z−q3(q1x+q2y+q3z)k虚四元数的实部为零,所以只需要重点关注实数部分求和是否为0即可:=q02+q12+q22+q32q02x−q1(q1x+q2y+q3z)i+q02+q12+q22+q32q02y−q2(q1x+q2y+q3z)j+q02+q12+q22+q32q02z−q3(q1x+q2y+q3z)k
实部为0,转换后仍对应到一个三维空间点,证毕。
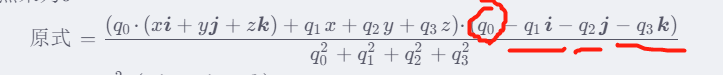

叉乘实在反应不过来,还是老老实实点乘算吧🤣
方法二: 套两次格拉斯曼积 公式
对于 q = [ s , v ] T = [ q 0 , v q ] T \bm{q}=[s, \bm{v}]^T=[q_0, \bm{v}_q]^T q=[s,v]T=[q0,vq]T,
p = [ 0 , v ] T = [ 0 , v p ] T \bm{p}=[0, \bm{v}]^T=[0, \bm{v}_p]^T p=[0,v]T=[0,vp]T
——————
其中
v q = [ q 1 , q 2 , q 3 ] T \bm{v}_q = [q_1, q_2, q_3]^T vq=[q1,q2,q3]T,
v p = [ x , y , z ] T \bm{v}_p = [x, y, z]^T vp=[x,y,z]T
要套个公式。。。

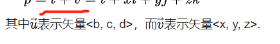
q
p
=
\bm{qp}=
qp= 两实部乘积 - 两虚部各自转置的点乘 + p实部·q虚部转置 + q实部·p虚部转置+ q虚部转置 × p虚部转置
q
p
=
0
⋅
q
0
−
v
q
T
⋅
v
p
T
+
q
0
⋅
v
p
T
+
0
⋅
v
q
T
+
v
q
T
×
v
p
T
=
−
v
q
T
⋅
v
p
T
+
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
\begin{align*}\bm{qp} &= 0·q_0-\bm{v}_q^T·\bm{v}_p^T+q_0·\bm{v}_p^T+0·\bm{v}_q^T+\bm{v}_q^T\times\bm{v}_p^T\\ & =-\bm{v}_q^T·\bm{v}_p^T+q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T \end{align*}
qp=0⋅q0−vqT⋅vpT+q0⋅vpT+0⋅vqT+vqT×vpT=−vqT⋅vpT+q0⋅vpT+vqT×vpT
p
′
=
q
p
q
−
1
=
q
p
q
∗
/
∣
∣
q
∣
∣
2
=
[
−
v
q
T
⋅
v
p
T
,
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
]
T
⋅
[
q
0
,
−
v
q
]
T
∣
∣
q
∣
∣
2
=
−
v
q
T
⋅
v
p
T
⋅
q
0
−
(
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
)
T
⋅
(
−
v
q
)
T
−
v
q
T
⋅
v
p
T
⋅
(
−
v
q
)
T
+
(
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
)
T
q
0
+
(
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
)
T
×
(
−
v
q
)
T
∣
∣
q
∣
∣
2
其中的实部为:
实部
=
−
v
q
T
⋅
v
p
T
⋅
q
0
−
(
q
0
⋅
v
p
T
+
v
q
T
×
v
p
T
)
T
⋅
(
−
v
q
)
T
+
(
v
q
T
×
v
p
T
)
T
×
(
−
v
q
)
T
∣
∣
q
∣
∣
2
=
−
v
q
T
⋅
v
p
T
⋅
q
0
+
q
0
⋅
v
p
T
⋅
v
q
T
+
(
v
q
T
×
v
p
T
)
T
⋅
v
q
T
−
(
v
q
T
×
v
p
T
)
T
×
v
q
T
∣
∣
q
∣
∣
2
=
0
\begin{align*}\bm{p}^\prime &= \bm{qpq^{-1}} \\ &= \bm{qpq^*/||q||^2}\\ &= \frac{[-\bm{v}_q^T·\bm{v}_p^T, q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T]^T·[q_0, -\bm{v}_q]^T}{||q||^2} \\ &= \frac{-\bm{v}_q^T·\bm{v}_p^T·q_0-(q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T)^T·(-\bm{v}_q)^T-\bm{v}_q^T·\bm{v}_p^T·(-\bm{v}_q)^T+(q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T)^Tq_0+(q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T)^T×(-\bm{v}_q)^T}{||q||^2} \\ & 其中的实部为:\\ 实部&= \frac{-\bm{v}_q^T·\bm{v}_p^T·q_0-(q_0·\bm{v}_p^T+\bm{v}_q^T\times\bm{v}_p^T)^T·(-\bm{v}_q)^T+(\bm{v}_q^T\times\bm{v}_p^T)^T×(-\bm{v}_q)^T}{||q||^2} \\ &= \frac{-\bm{v}_q^T·\bm{v}_p^T·q_0+q_0·\bm{v}_p^T·\bm{v}_q^T+(\bm{v}_q^T\times\bm{v}_p^T)^T·\bm{v}_q^T-(\bm{v}_q^T\times\bm{v}_p^T)^T×\bm{v}_q^T}{||q||^2}\\ & = 0 \end{align*}
p′实部=qpq−1=qpq∗/∣∣q∣∣2=∣∣q∣∣2[−vqT⋅vpT,q0⋅vpT+vqT×vpT]T⋅[q0,−vq]T=∣∣q∣∣2−vqT⋅vpT⋅q0−(q0⋅vpT+vqT×vpT)T⋅(−vq)T−vqT⋅vpT⋅(−vq)T+(q0⋅vpT+vqT×vpT)Tq0+(q0⋅vpT+vqT×vpT)T×(−vq)T其中的实部为:=∣∣q∣∣2−vqT⋅vpT⋅q0−(q0⋅vpT+vqT×vpT)T⋅(−vq)T+(vqT×vpT)T×(−vq)T=∣∣q∣∣2−vqT⋅vpT⋅q0+q0⋅vpT⋅vqT+(vqT×vpT)T⋅vqT−(vqT×vpT)T×vqT=0
啊~~~我还是点乘吧🤣
√ 题4
4、画表总结 旋转矩阵、轴角、欧拉角、四元数的转换关系。
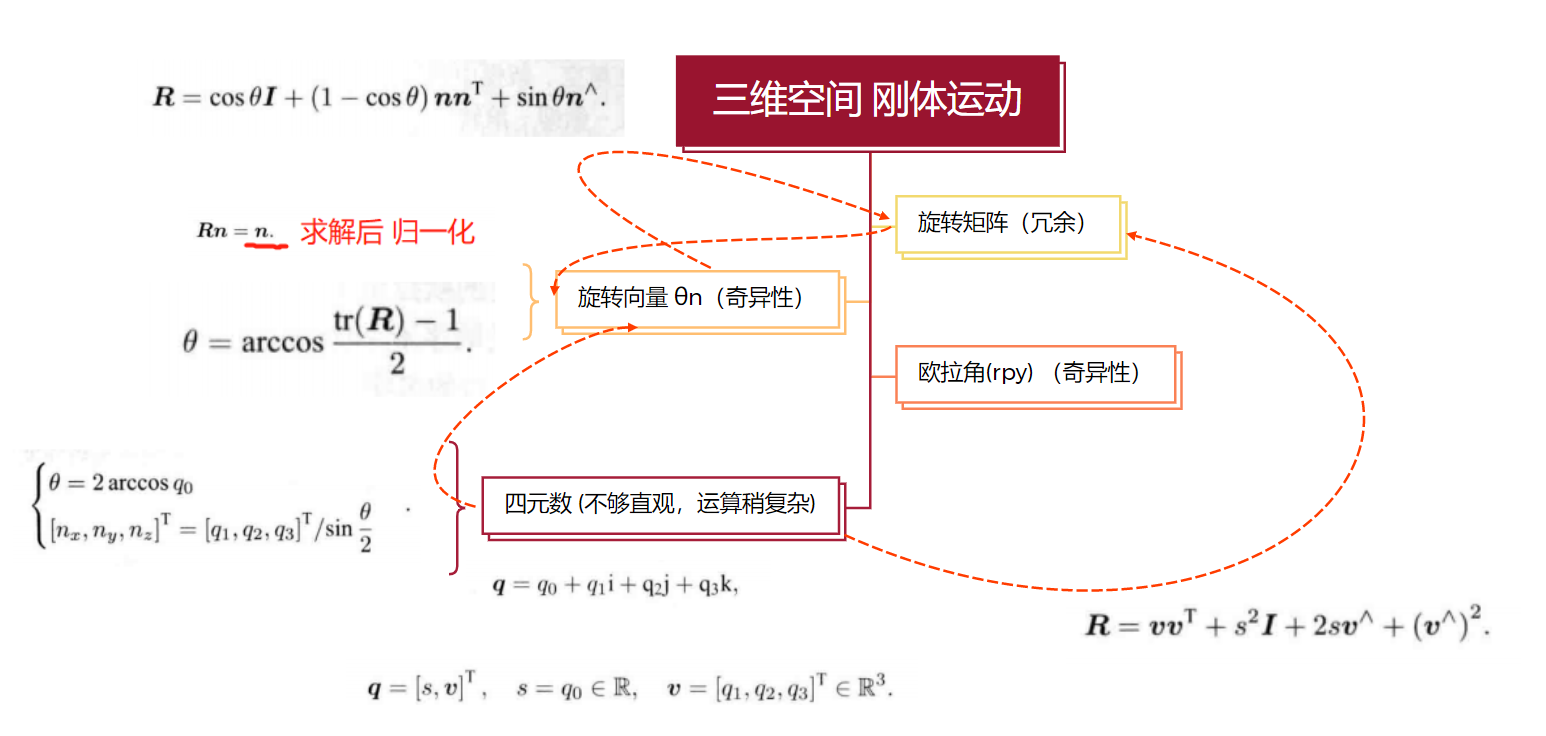
维基百科链接
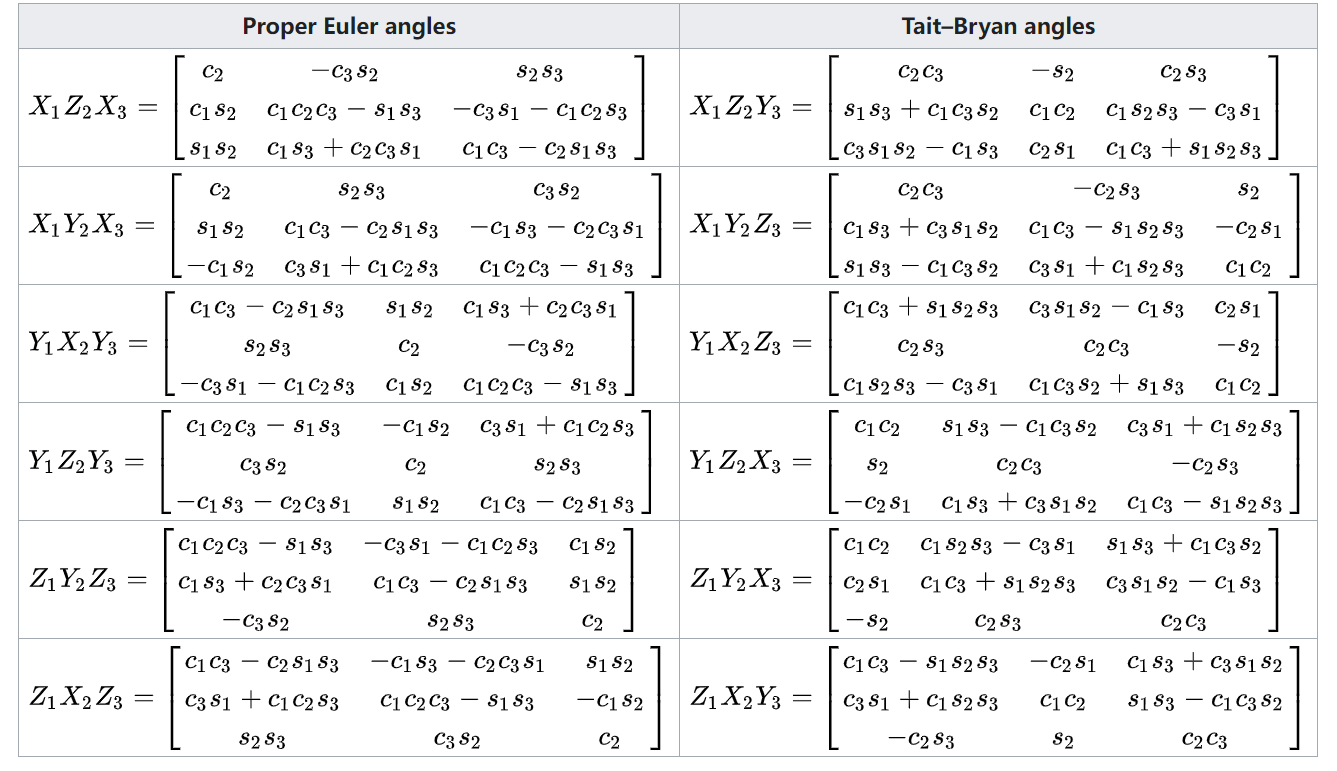

√ 题5
5、假设有一个大的 Eigen 矩阵,想把它的左上角 3 × 3 的块取出来,然后赋值为
I
3
×
3
\bm{I}_{3 × 3}
I3×3 。请编程实现。
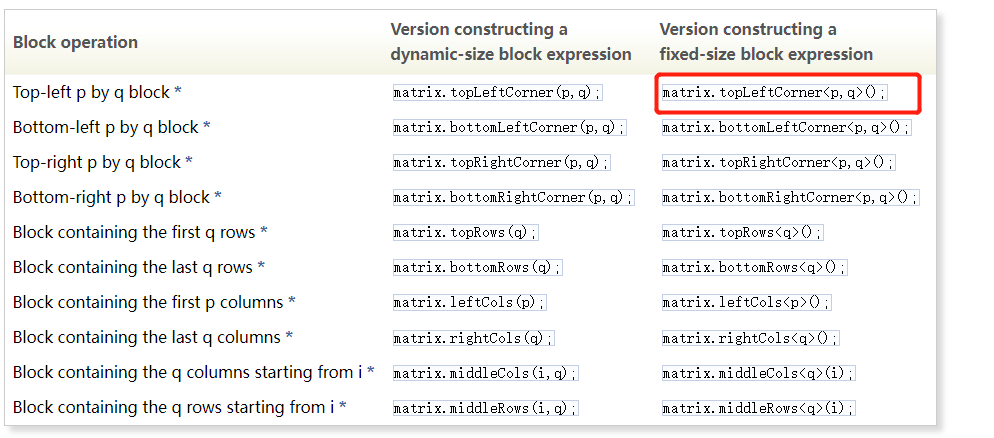
块操作官方文档

#include <iostream>
#include <Eigen/Core>
using namespace std;
using namespace Eigen;
#define MATRIX_SIZE 6
int main() {
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrxi_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
cout << matrxi_NN << endl;
// 取左上角 3 * 3 输出
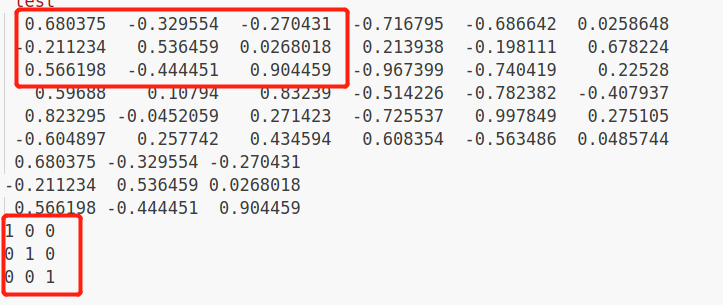
cout << matrxi_NN.block<3,3>(0,0) << endl; // 其中0,0为起始点坐标,第一个3为向下走3个,第二个3是向左走三个 构成的矩阵块
matrxi_NN.block<3, 3>(0, 0) = Matrix3d::Identity(); // 更新 某块的值 为 单位矩阵块
cout << matrxi_NN.block<3,3>(0,0)<< endl; // 再次输出 左上角的 块
return 0;
}
#include <iostream>
#include <Eigen/Core>
using namespace std;
using namespace Eigen;
#define MATRIX_SIZE 6
int main() {
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrxi_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
cout << matrxi_NN << endl;
/* 方法2:不够灵活 */
// 取左上角 3 * 3块 输出
cout << matrxi_NN.topLeftCorner(3,3) << endl;
matrxi_NN.topLeftCorner(3,3) = Matrix3d::Identity(); // 更新 某块的值 为 单位矩阵块
cout << matrxi_NN.block<3,3>(0,0)<< endl; // 再次输出 左上角的 块
return 0;
}
题6
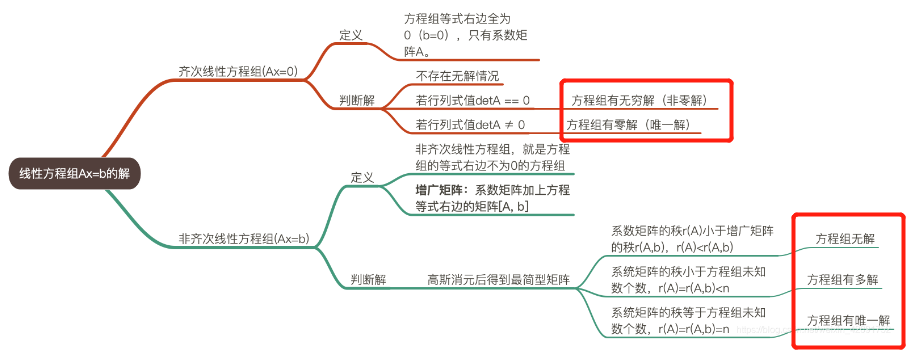
6、一般线性方程 A x = b \bm{Ax=b} Ax=b有哪几种做法?你能在Eigen中实现吗?
待做:
- 进一步了解每种求解方法的原理
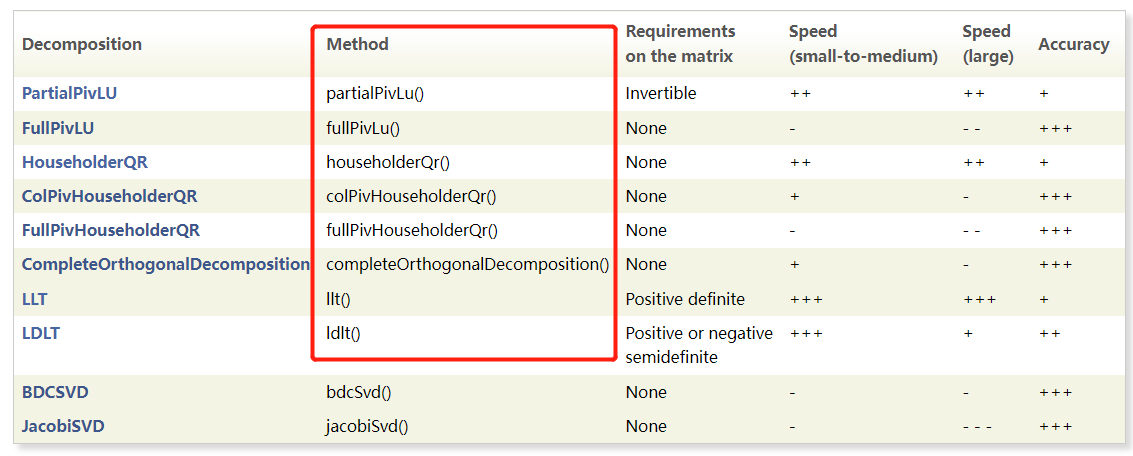
Ax=b求解Eigen官方文档链接
Eigen 提供了 8种API
使用 Eigen 求解线性最小二乘系统。有一个超定方程组,比如
A
x
=
b
\bm{Ax=b}
Ax=b 没有解。在这种情况下,搜索最接近解的向量
x
\bm{x}
x 是有意义的,使此时的差值
A
x
−
b
\bm{Ax-b}
Ax−b 尽可能小。这个
x
\bm{x}
x 称为最小二乘解(如果使用欧几里得范数)。后两种方法用于 求解 无解的情况
#include <iostream>
#include <Eigen/Core>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
#define MATRIX_SIZE 3
// 参考 P50 代码
int main(int argc, char **argv) {
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN
= MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
Matrix<double, MATRIX_SIZE, MATRIX_SIZE> A = matrix_NN * matrix_NN.transpose(); // 保证 半正定
Matrix<double, MATRIX_SIZE, 1> b = MatrixXd::Random(MATRIX_SIZE, 1);
//直接求逆
Matrix<double, MATRIX_SIZE, 1> x = A.inverse() * b;
cout << "直接求逆 得到的x为: " << x.transpose() << endl;
/*综合首选:ColPivHouseholderQR ,无要求/准确/速度还行*/
Matrix<double, MATRIX_SIZE, 1> x4 = A.colPivHouseholderQr().solve(b);
cout << "1、ColPivHouseholderQR 求解得到的x为: " << x4.transpose() << endl;
/* 矩阵 对称且正定 LLT 或 LDLT*/ // 快 +++ 要求正定
//LLT分解 正定
Matrix<double, MATRIX_SIZE, 1> x7 = A.llt().solve(b);
cout << "2、LLT 求解得到的x为: " << x7.transpose() << endl;
//LDLT分解, 最低 负正定 LDLt Cholesky
Matrix<double, MATRIX_SIZE, 1> x8 = A.ldlt().solve(b);
cout << "3、LDLT 求解得到的x为: " << x8.transpose() << endl;
/* 矩阵 满秩 非对称 PartialPivLU */ // 要求可逆 速度 ++
Matrix<double, MATRIX_SIZE, 1> x1 = A.partialPivLu().solve(b); // A.lu().solve(b) 等效
cout << "4、PartialPivLU 求解得到的x为: " << x1.transpose() << endl;
// 其他 QR分解
Matrix<double, MATRIX_SIZE, 1> x3 = A.householderQr().solve(b);
cout << "5、HouseholderQR 求解得到的x为: "<< x3.transpose() << endl;
Matrix<double, MATRIX_SIZE, 1> x5 = A.fullPivHouseholderQr().solve(b);
cout << "6、FullPivHouseholderQR 求解得到的x为: "<< x5.transpose() << endl;
Matrix<double, MATRIX_SIZE, 1> x6 = A.completeOrthogonalDecomposition().solve(b);
cout << "7、CompleteOrthogonalDecomposition 求解得到的x为: "<< x6.transpose() << endl;
//其他 LU分解
Matrix<double, MATRIX_SIZE, 1> x2 = A.fullPivLu().solve(b);
cout << "8、FullPivLU 求解得到的x为: " << x2.transpose() << endl;
return 0;
}

——————参考资料:
参考 P50 (第50页) 的代码。
LLT要求最严苛: 正定
官网LLT示例代码:
#include <iostream>
#include <Eigen/Dense>
int main()
{
Eigen::Matrix2f A, b;
Eigen::LLT<Eigen::Matrix2f> llt;
A << 2, -1, -1, 3;
b << 1, 2, 3, 1;
std::cout << "Here is the matrix A:\n" << A << std::endl;
std::cout << "Here is the right hand side b:\n" << b << std::endl;
std::cout << "Computing LLT decomposition..." << std::endl;
llt.compute(A);
std::cout << "The solution is:\n" << llt.solve(b) << std::endl;
A(1,1)++;
std::cout << "The matrix A is now:\n" << A << std::endl;
std::cout << "Computing LLT decomposition..." << std::endl;
llt.compute(A);
std::cout << "The solution is now:\n" << llt.solve(b) << std::endl;
}
Eigen(http://eigen.tuxfamily.org)是常用的 C++ 矩阵运算库,具有很高的运算效率。大部分需要在 C++ 中使用矩阵运算的库,都会选用 Eigen 作为基本代数库,例如 Google Tensorflow,Google Ceres,GTSAM 等。

高斯消元法: 加减消元、回代求未知数值
官方文档: http://eigen.tuxfamily.org/dox/group__TutorialLinearAlgebra.html
#include<iostream>
#include<Eigen/Dense>
using namespace std;
using namespace Eigen;
int main(){
// 线性方程求解 Ax = b
/* 以 解 唯一 示例 多解情况 不好判断*/
Matrix3f A;
A << 1, 2, 3, 4, 5, 6, 7, 8, 10;
Vector3f b(3, 3, 4);
// https://eigen.tuxfamily.org/index.php?title=API_Showcase#Linear_solving
Vector3f ans1 = A.lu().solve(b); // using partial-pivoting LU
Vector3f ans2 = A.fullPivLu().solve(b); // using full-pivoting LU
Vector3f ans3 = A.householderQr().solve(b); // using Householder QR
Vector3f ans4 = A.ldlt().solve(b); // using LDLt Cholesky
cout << "partial-pivoting LU: " << ans1.transpose() << endl;
cout << "full-pivoting LU: " << ans2.transpose() << endl;
cout << "Householder QR: "<< ans3.transpose() << endl;
cout << "LDLt Cholesky: " << ans4.transpose() << endl; // 这里的A 不满足正定,故求解有误
return 0;
}

#include <iostream>
#include <Eigen/Dense>
//using namespace std;
//using namespace Eigen;
int main()
{
Eigen::Matrix3f A;
Eigen::Vector3f b; // 向量 定义
A << 1,2,3, 4,5,6, 7,8,10; // 矩阵 初始化
b << 3, 3, 4;
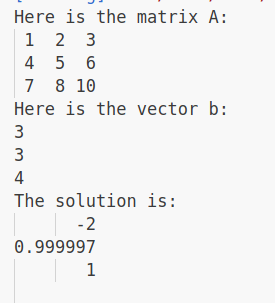
std::cout << "Here is the matrix A:\n" << A << std::endl; // 矩阵 和 向量 都可以直接输出
std::cout << "Here is the vector b:\n" << b << std::endl;
Eigen::Vector3f x = A.colPivHouseholderQr().solve(b);
std::cout << "The solution is:\n" << x << std::endl;
}
第13行 等效写法:
ColPivHouseholderQR<Matrix3f> dec(A);
Vector3f x = dec.solve(b);
ColPivHouseholderQR是一个带有列枢轴的QR分解。这是一个很好的折衷方案,因为它**适用于所有矩阵,同时速度相当快。**下面是一些其他分解的表格,你可以从中选择,这取决于你的矩阵,你想要解决的问题,以及你想要做出的权衡:
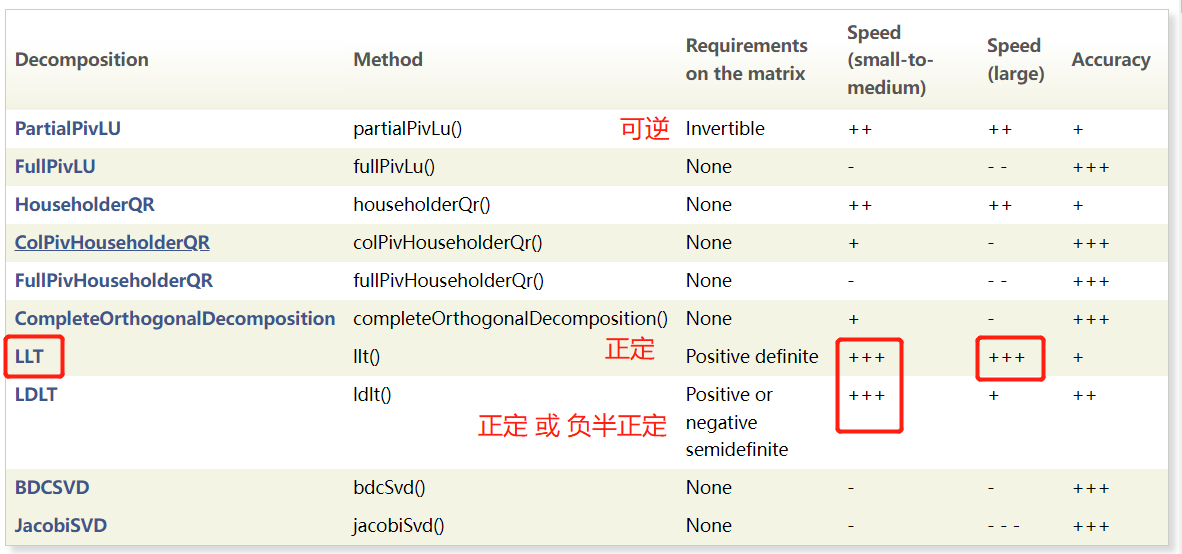
无要求、准确且 速度还行:
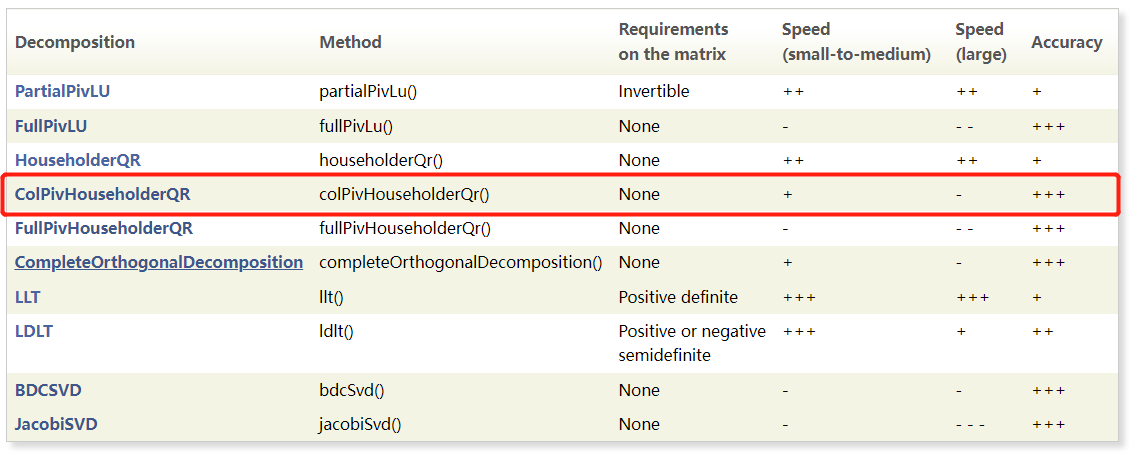
对于求解具有满秩非对称矩阵的线性系统,一个很好的选择是PartialPivLU。
矩阵是对称且正定的,一个很好的选择是LLT或LDLT分解。
正定必可逆









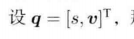

















 997
997











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








