👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
将直接三维有限差分时域(FDTD)方法应用于各种微带结构的全波分析。该方法被证明是模拟复杂微带电路元件和微带天线的有效工具。根据时域结果计算了线馈矩形贴片天线的输入阻抗以及低通滤波器和支线耦合器的频率相关散射参数。这些电路是捏造的,对它们的测量结果与FDTD结果进行了比较,并显示出良好的一致性。
基于FDTD方法的微带结构全波分析研究
一、FDTD方法基本原理与算法实现
1.1 麦克斯韦方程组的离散化
FDTD方法通过二阶中心差分法对麦克斯韦旋度方程进行时空离散化。Yee网格(1966年提出)采用电场分量与磁场分量的空间交错布局(电场位于网格边中心,磁场位于面中心),形成蛙跳式时间迭代模式。
磁场分量则用前半个时间步的电场值更新。
1.2 数值稳定性条件
Courant-Friedrichs-Lewy (CFL)稳定性条件要求:

其中c为光速,Δx、Δy、Δz为空间步长。该条件限制了最大时间步长,在微带结构分析中需特别注意薄介质层的网格划分。
1.3 激励源设置
微带结构常用激励方式包括:
- 硬源注入:直接指定源节点的场值(如高斯脉冲)
- 电流源:通过J项引入激励
- 总场/散射场分离:适用于开放空间辐射问题
二、微带结构建模关键技术
2.1 几何参数与电磁特性
微带线的特性阻抗Z0和相速vp由介质基板参数(εr, h)及导体宽度W决定,准TEM波近似下:

其中有效介电常数εeff随W/h变化。复杂结构如电磁带隙(EBG)单元可通过等效LC电路建模,其谐振频率由几何参数调控。
2.2 多尺度网格划分策略
| 技术类型 | 特点 | 适用场景 |
|---|---|---|
| 均匀网格 | 简单易实现,但计算效率低 | 简单微带线分析 |
| 非均匀子网格 | 局部加密(如边缘场强区域),时间步长自适应优化,节省40%以上计算资源 | 高频/精细结构分析 |
| 动态自适应网格 | 实时调整网格密度,最大边长比可达64:1 | 复杂拓扑结构(如环形谐振器) |
2.3 边界条件配置
- 金属边界:PEC(完美电导体)用于模拟微带线导体层
- 开放边界:采用Berenger PML(完美匹配层),反射率低于-60dB
- 周期边界:减少计算域尺寸,适用于阵列结构分析
三、数值误差控制与优化
3.1 色散误差抑制技术
- 高阶FDTD(2,4) :空间四阶差分,允许网格尺寸增大2倍而不降低精度
- 辛时域算法:引入可逆传播算子,长期仿真误差积累降低70%
- ADI-FDTD:无条件稳定算法,时间步长突破CFL限制,适用于低频段分析
3.2 介质界面处理
采用等效介质参数法处理微带基板非均匀性,在Yee网格单元内进行介电常数加权平均,减少界面处的场突变误差。
四、典型验证案例与结果分析
4.1 矩形微带贴片天线仿真
| 参数 | 仿真值 | 实测值 | 误差 |
|---|---|---|---|
| 谐振频率(GHz) | 2.45 | 2.48 | +1.2% |
| 回波损耗(dB) | -21.3 | -19.8 | -7.1% |
| 增益(dBi) | 7.2 | 6.9 | -4.2% |
| FDTD仿真准确再现了时域场分布(图1)及远场方向图特性。 |
五、研究进展与工程应用
5.1 算法加速技术
- GPU并行计算:利用CUDA架构实现百倍加速比,支持百万级网格实时仿真
- 混合算法:FDTD与矩量法(MoM)耦合,提升大尺寸结构计算效率
5.2 工业软件实现
Altair Feko等商用工具集成FDTD求解器,支持:
- 多层基板自动建模
- S参数自动提取
- 与电路仿真器协同优化
六、研究挑战与未来方向
- 多物理场耦合:热-电-机械效应对高频微带结构的影响建模
- 人工智能辅助:基于深度学习的网格参数自动优化
- 超材料集成:电磁带隙/超表面与微带线的新型复合结构设计
📚2 运行结果
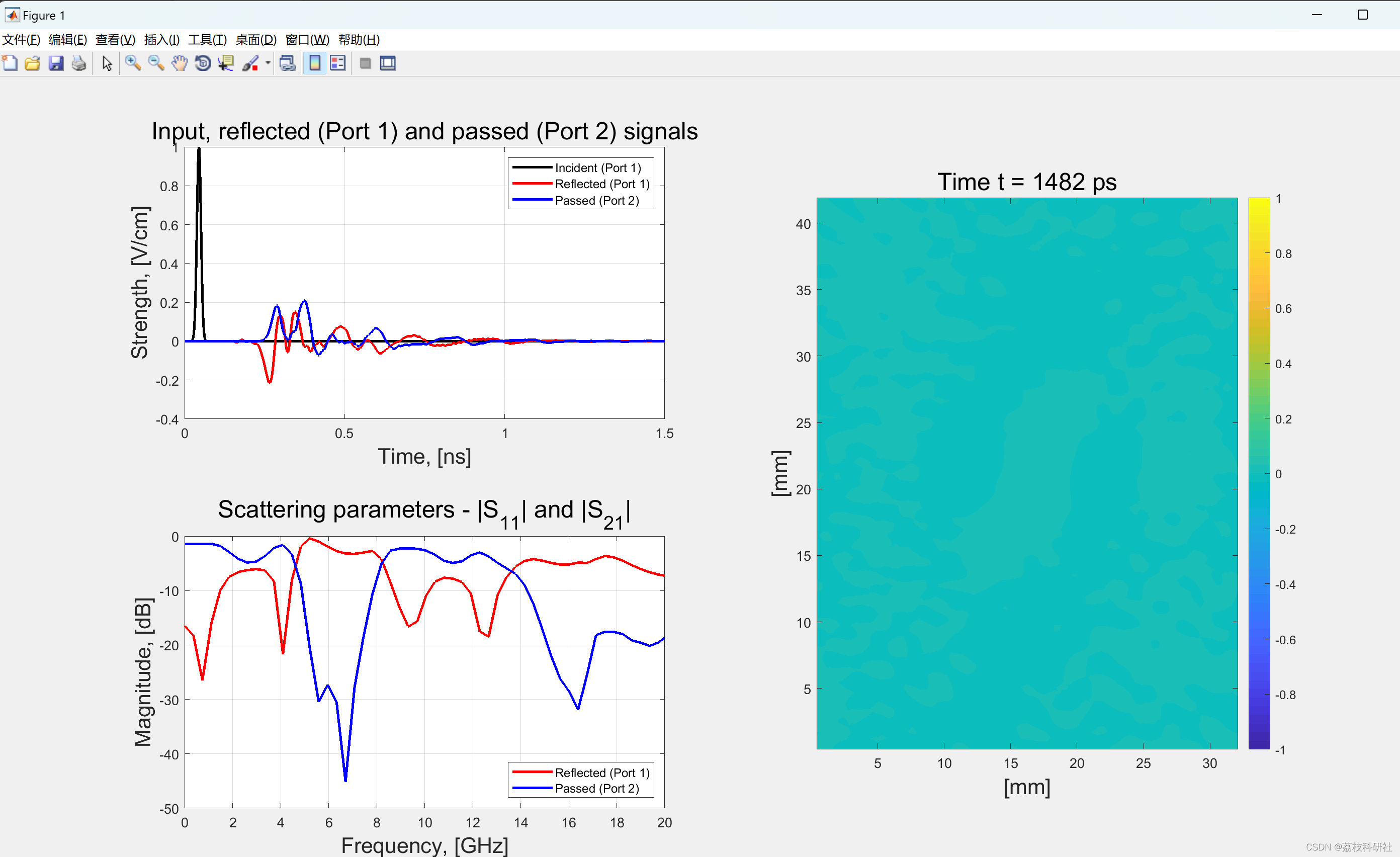
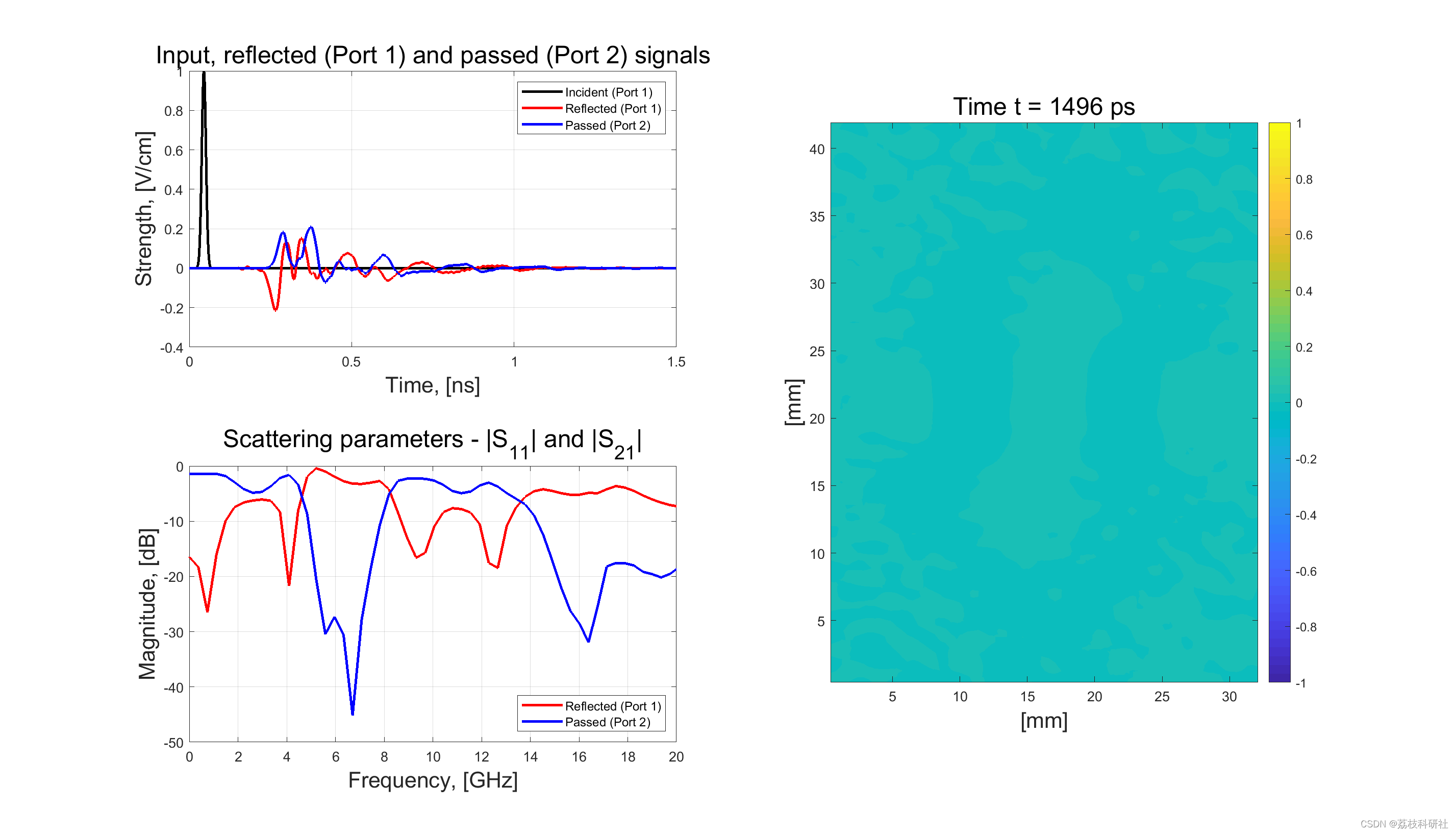
部分代码:
%% Current code includes some improvements in comparison with the original
%% calculations:
% 1) imposing UPML instead of Mur ABCs;
% 2) using real metal (copper) as a patch conductor material instead of PEC;
% 3) applying matched load at the ends of filter's transmission microstrip
% lines to prevent physical reflections;
% 4) no "magnetic wall" or "electric wall" conditions at the Ez source plane.
%
function FDTD_3D_Lowpass
close all; clear; clc;
%% Physical constants
epsilon0 = 8.85418782e-12; mu0 = 1.25663706e-6;
c = 1.0/sqrt(mu0*epsilon0);
%% Gaussian half-width
t_half = 15.0e-12;
%% Microstrip transmission lines parameters
lineW = 2.413e-3;
lineH = 1.0e-3;
lineEr = 2.2;
Z0 = 49.2526;
%% End time
t_end = 1.5e-9;
%% Total mesh dimensions and grid cells sizes (without PML)
nx = 80; ny = 100; nz = 16;
dx = 0.4064e-3; dy = 0.4233e-3; dz = 0.2650e-3;
%% Number of PML layers
PML = 5;
%% Matrix of material's constants
number_of_materials = 4;
% For material of number x = 1,2,3... :
% Material(x,1) - relative permittivity, Material(x,2) - relative permeability,
% Material(x,3) - specific conductivity
% Vacuum
Material(1,1) = 1.0; Material(1,2) = 1.0; Material(1,3) = 0.0;
% Metal (Copper)
Material(2,1) = 1.0; Material(2,2) = 1.0; Material(2,3) = 5.88e+7;
% Substrate material (RT/Duroid 5880)
Material(3,1) = lineEr; Material(3,2) = 1.0; Material(3,3) = 0.0;
% Matched load material is calculated from transmission line parameters
Material(4,1) = 1.0; Material(4,2) = 1.0; Material(4,3) = lineH/(Z0*lineW*dy);
% Add PML layers
nx = nx + 2*PML; ny = ny + 2*PML; nz = nz + 2*PML;
% Calculate dt
dt = (1.0/c/sqrt( 1.0/(dx^2) + 1.0/(dy^2) + 1.0/(dz^2)))*0.9999;
number_of_iterations = ceil(t_end/dt);
%% 3D array for geometry
Index = ones(nx, ny, nz);
%% Define of low-pass filter geometry
% Ground plane
Index((1+PML):(nx-PML), (1+PML):(ny-PML), PML+1) = 2;
% Rectangular patch (one cell thickness)
Index((nx/2-25):(nx/2+25), (ny/2-3):(ny/2+3), PML+5) = 2;
% Transmission line from port 1 to rectangular patch
Index((nx/2-10):(nx/2-5), (PML+1):ny/2, PML+5) = 2;
% Transmission line from rectangular patch to port 2
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。


























 208
208

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










