💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
Koopman-MPC框架:基于数据驱动的四旋翼无人机控制研究
💥1 概述
摘要
本文提出了一种基于Koopman算子和扩展动态模态分解(EDMD)的四旋翼无人机学习和控制的新型数据驱动方法。基于常规方法如欧拉角(表示方向)构建EDMD的可观测量已知涉及奇异性。为解决这一问题,我们采用基于非线性系统底层拓扑的一组信息物理可观测量。我们使用旋转矩阵直接表示方向动态,并在SE(3)流形中获得非线性四旋翼动态的抬升线性表示。这种EDMD模型能够进行准确预测,并且能够推广到多个验证集。此外,我们基于提出的EDMD模型设计了一个线性模型预测控制器(MPC)来跟踪敏捷的参考轨迹。模拟结果显示,所提出的MPC控制器的运行速度可达100赫兹,并且能够以很高的准确性跟踪任意参考轨迹。
设计非线性机器人系统的最优控制器是一个具有挑战性的问题。目标是开发一个能够稳定系统并遵循参考轨迹的控制器,同时遵守由系统动态和执行器限制引起的约束。模型预测控制(MPC)是一种基于优化的方法,可以用于实现这一目标(Rawlings等人(2017);Berberich等人(2022))。指定性能指标和约束的能力使得在设计非线性系统控制器时非常直观。尽管最近优化技术和计算能力的进步(Kouzoupis等人(2018);Gros等人(2020))已经使得实时实现非线性模型预测控制器(NMPC)成为可能,但它们仍然需要足够精确的数学模型,并且无法处理模型不确定性。为了解决其中一些问题,Hou和Wang(2013);Hewing等人(2019);Krolicki等人(2022)已经开发了数据驱动技术,而Lusch等人(2018);Han等人(2020);Wang等人(2021)则开发了基于学习的方法来识别系统的潜在模型。然而,这些方法计算密集且不能应用于一般的高维非线性系统。为了克服与NMPC相关的问题,我们提出了一种基于Koopman算子的方法,用于学习受控非线性动态系统的线性预测器。Koopman算子控制一组可观测函数的演变,这些函数可以被解释为非线性。
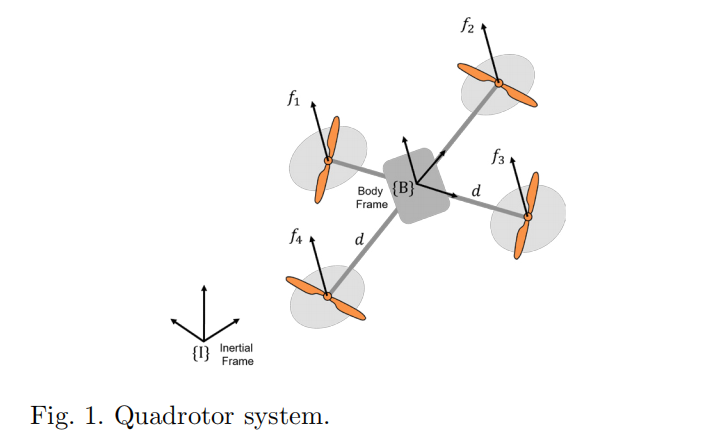
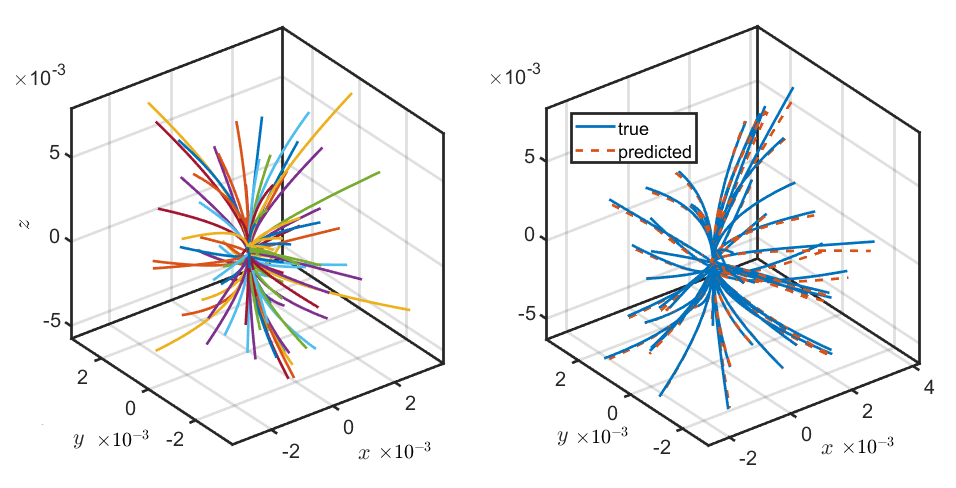
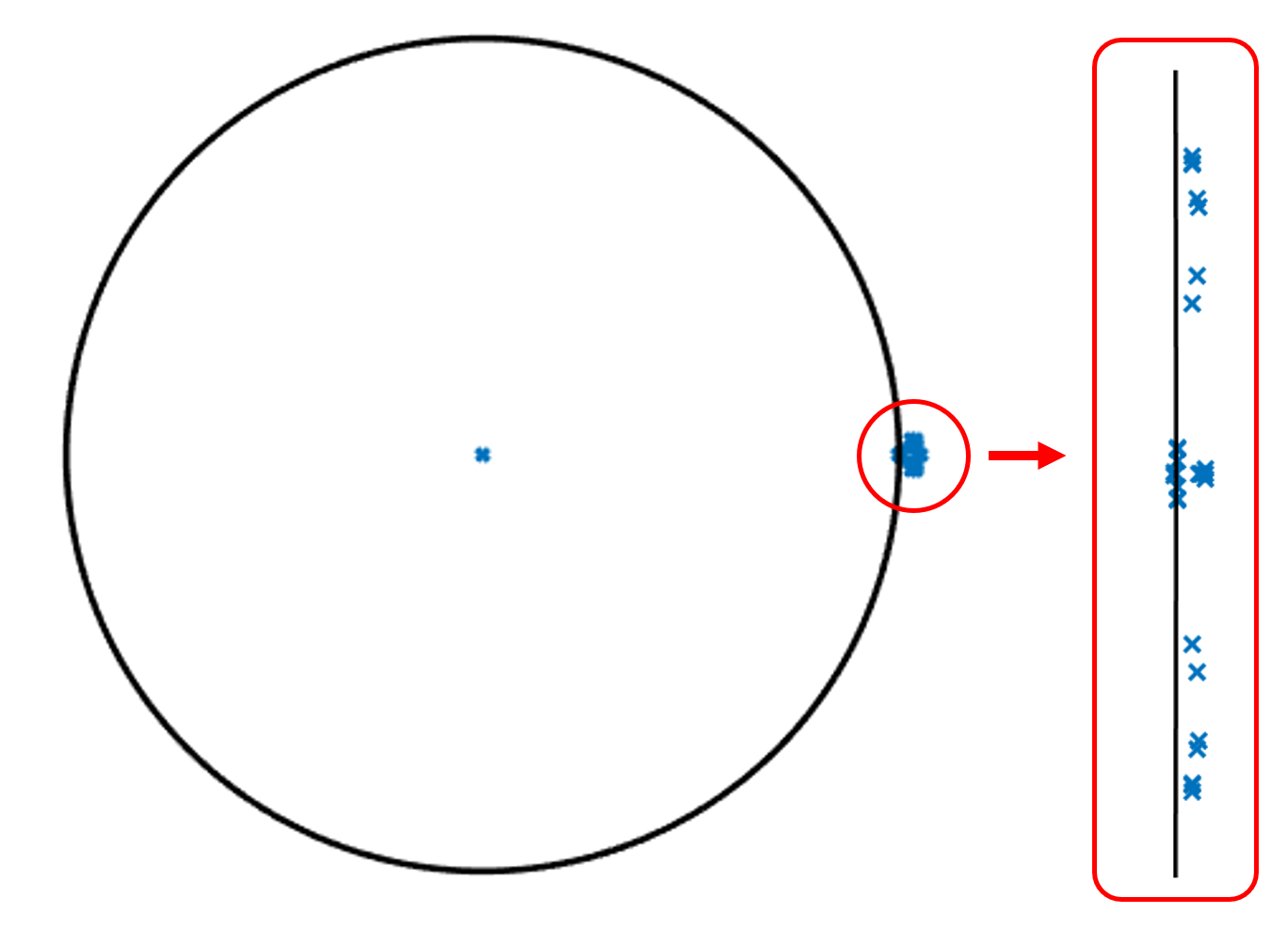
在本工作中,我们提出了一组物理信息驱动的可观测量,可用于获得非线性三维四旋翼系统的线性预测器。这些可观测量函数是通过旋转矩阵和角速度的乘积构造的。将这组可观测量与线性状态相结合,确保提升后的系统保留了原始非线性系统的底层 SE(3) 拓扑结构。我们证明,使用 EDMD 学习到的线性预测器能够以合理的精度(平均误差为4.5%)预测任意随机轨迹。此外,我们利用学习到的线性预测器设计了一个用于跟踪参考轨迹的控制器。为此,我们在提升的状态空间中开发了一个线性模型预测控制(MPC)。所提出的 SE(3) MPC 框架可以在实时环境下以100赫兹的频率运行,并能够以适当的表现跟踪任意随机参考轨迹。未来的研究将结合 EDMD 与在线学习,以便在存在未知干扰(如风)的情况下跟踪轨迹。
Koopman-MPC框架:基于数据驱动的四旋翼无人机控制研究
一、Koopman算子理论与非线性系统线性化
Koopman算子是一种将非线性系统映射到高维线性空间的理论工具,其核心思想是通过线性动力学近似非线性系统,从而利用成熟的线性控制方法(如LQR、MPC)实现复杂系统的控制。
- 基本要素:
- Koopman本征函数:作为基向量,将系统状态投影到新的线性空间;
- Koopman特征值:反映系统动态特性(如稳定性、振荡频率);
- Koopman模式:用于将投影后的状态还原到原始空间。
- 优势:
- 全局线性化:避免传统局部线性化(如雅可比矩阵)的局限性,适用于强非线性系统(如四旋翼无人机);
- 数据驱动特性:可通过动态模式分解(DMD)或扩展动态模式分解(EDMD)直接从数据中学习;
- 预测能力:通过特征值的幂次运算,可预测系统在多个时间步的状态演化。
二、模型预测控制(MPC)的核心原理
MPC是一种基于滚动优化的控制策略,其核心步骤包括预测模型构建、滚动优化与反馈校正:
- 预测模型:利用系统动力学模型(如Koopman线性模型)预测未来状态;
- 优化目标:最小化代价函数(如跟踪误差、控制输入能耗),同时考虑约束条件(如执行器饱和);
- 实时性:仅执行优化序列的第一个控制输入,并在下一时刻重新计算,适应动态变化。
MPC在四旋翼控制中的优势在于处理多输入多输出(MIMO)系统、显式处理约束,以及对模型误差的鲁棒性。
三、四旋翼无人机的动力学建模挑战
四旋翼的动力学特性使其控制问题极具挑战性:
- 非线性与欠驱动:仅有4个控制输入(电机转速)需控制6个自由度,导致强耦合效应;
- 环境干扰敏感性:风扰、传感器噪声等外部因素影响姿态稳定性;
- 复杂气动效应:旋翼产生的非定常气流导致模型不确定性,尤其在高速机动时显著。
传统PID控制依赖精确模型且难以处理非线性,而基于模型的MPC面临实时计算复杂度高的问题。
四、Koopman-MPC框架的构建与实现
Koopman-MPC通过结合Koopman算子的线性化能力与MPC的优化特性,为四旋翼控制提供新思路:
- 数据驱动的Koopman模型学习:
- 使用EDMD或深度学习(如神经网络)从飞行数据中提取Koopman算子的有限维近似;
- 引入旋转矩阵等物理可观测量,避免欧拉角奇异性,提升模型泛化能力。
- 线性MPC设计:
- 基于Koopman模型构建线性状态空间方程,简化MPC的二次规划问题;
- 实验表明,控制器可在100Hz频率下实时运行,跟踪误差低于传统非线性MPC。
- 应用案例:
- 在SE(3)流形上实现四旋翼的全局线性化,支持高速轨迹跟踪(如8字形轨迹);
- 结合高斯过程回归(GP)与递归多元回归,提升模型在风扰下的鲁棒性。
五、数据驱动方法的关键技术
- 动态模式分解(DMD)与EDMD:
- DMD通过数据快照对近似Koopman特征值,EDMD引入非线性基函数提升精度;
- EDMD在受控系统中扩展,支持含控制输入的Koopman模型。
- 深度学习增强:
- 使用递归神经网络(RNN)学习Koopman不变子空间,捕捉长期依赖性;
- 端到端强化学习框架联合优化Koopman嵌入与控制器,提升数据效率。
- 核方法与正则化:
- 核岭回归(KRR)与Nyström近似降低计算复杂度,适用于高维数据;
- Tikhonov正则化防止过拟合,提升模型泛化能力。
六、优势与挑战
- 优势:
- 计算高效:线性模型使MPC的优化问题转化为凸问题,计算速度提升10倍以上;
- 模型无关性:无需先验动力学模型,适应复杂气动效应与传感器噪声;
- 全局稳定性:通过Koopman特征值分析保证闭环系统的指数稳定性。
- 挑战:
- 可观测函数选择:基函数的选取影响模型精度,需结合物理知识与数据驱动优化;
- 实时数据需求:在线学习需高频传感器数据,对硬件算力要求较高;
- 多模态场景泛化:在极端飞行姿态(如翻转)下的模型泛化能力仍需验证。
七、未来研究方向
- 混合建模:融合物理模型与数据驱动方法,提升稀疏数据下的泛化能力;
- 分布式学习:在边缘计算架构中实现Koopman模型的在线更新与协同控制;
- 安全强化学习:结合Koopman-MPC与安全约束优化,保障高风险任务的安全性。
结语
Koopman-MPC框架通过数据驱动的非线性系统线性化,为四旋翼无人机的高效控制提供了理论创新与技术突破。其在实时性、鲁棒性和可扩展性方面的优势,使其在物流配送、灾害救援等复杂场景中展现出广阔应用前景。未来研究需进一步解决模型泛化与硬件集成问题,推动该技术从实验室走向实际部署。
📚2 运行结果


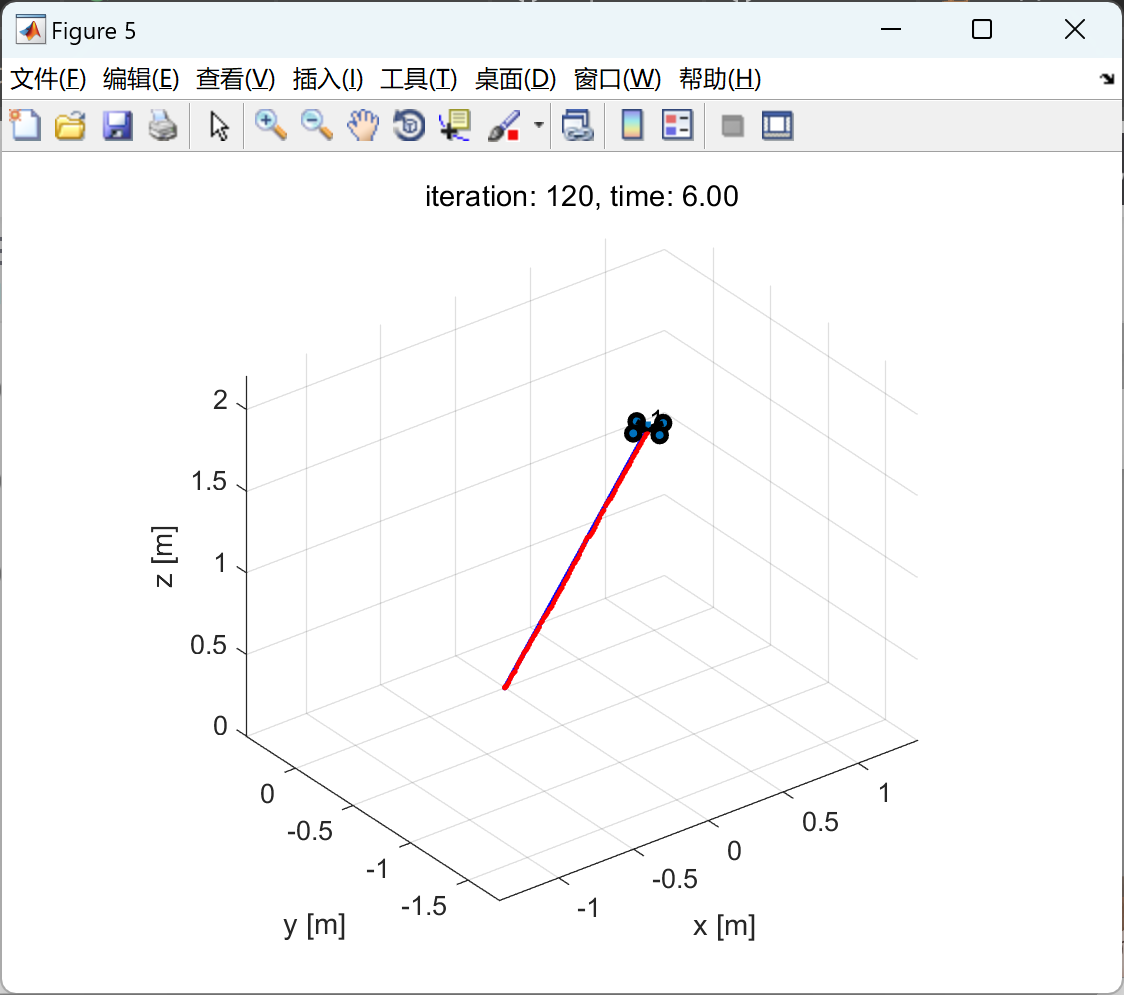

🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
Sriram S.K.S. Narayanan ∗, Duvan Tellez-Castro ∗, Sarang Sutavani ∗, Umesh Vaidya

























 3918
3918

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










