【IMU Kalman滤波器】9轴IMU传感器（加速度计、陀螺仪、磁力计）的卡尔曼滤波器算法研究（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

 ⛳️赠与读者

💥1 概述

9轴IMU传感器卡尔曼滤波器算法研究

一、9轴IMU传感器基础

二、卡尔曼滤波基础

三、传感器噪声模型与误差特性

四、卡尔曼滤波器设计

五、算法实现案例

六、挑战与解决方案

七、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据

---

 ⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时候，不要觉得这些问题搞笑。哲学是科学之母，哲学就是追究终极问题，寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能让人胸中升起一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它居然给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

     或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

9轴IMU传感器卡尔曼滤波器算法研究

一、9轴IMU传感器基础

1. 传感器组成与原理
   9轴IMU由加速度计（测量线性加速度）、陀螺仪（测量角速度）和磁力计（测量磁场方向）组成，提供三维空间中的运动与方向信息。

   • 加速度计通过惯性力检测加速度（牛顿第二定律），但易受高频噪声影响。
   • 陀螺仪基于科氏力测量角速度，但积分运算会导致低频漂移误差。
   • 磁力计通过霍尔效应检测地磁场方向，用于航向角（Yaw）校准，但对环境磁场干扰敏感。

2. 技术规格示例

   • 加速度计：测量范围±16g，分辨率0.98mg/LSB@±16g，噪声密度160μg/√Hz。

     

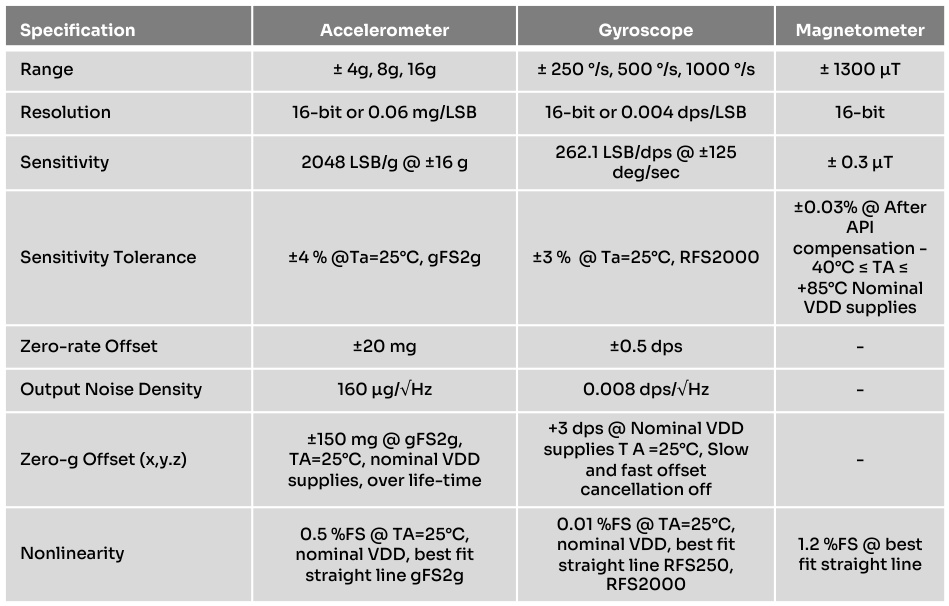
   • 陀螺仪：量程±2000dps，分辨率0.0038°/s/LSB@±250dps，温度误差±0.005°/(s·°C)。

     

   • 磁力计：量程±4900μT，分辨率0.15μT/LSB，动态响应特性良好。

---

二、卡尔曼滤波基础

1. 核心原理
   卡尔曼滤波通过预测-校正框架实现最优状态估计：
   • 预测：基于系统模型和上一时刻状态估计当前状态。
   • 校正：结合传感器观测值更新状态，通过卡尔曼增益平衡模型预测与测量数据的置信度。

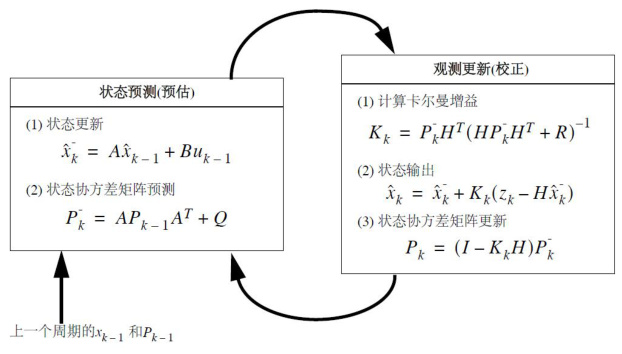
2. 关键方程

• 
  其中，Q为过程噪声协方差，R为观测噪声协方差。

---

三、传感器噪声模型与误差特性

传感器	噪声类型	误差特性	解决方案
加速度计	高频噪声（毛刺）	瞬时值不精确，姿态震荡	低通滤波或滑动平均
陀螺仪	低频漂移	积分累积误差，长期姿态偏移	磁力计/加速度计校正
磁力计	环境磁场干扰	航向角偏移（硬铁/软铁误差）	动态校准算法

典型噪声参数：

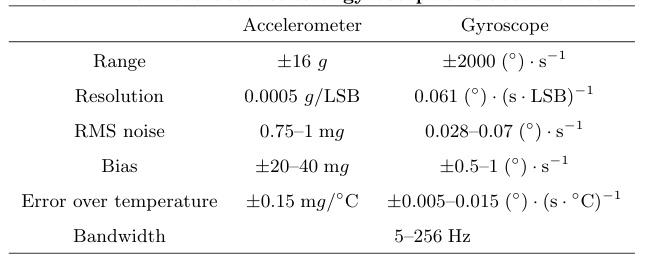
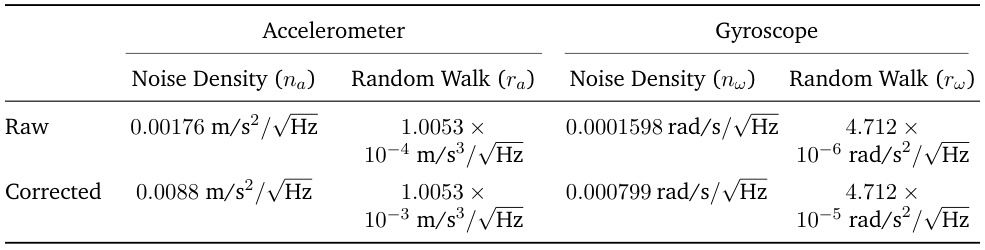
• 加速度计RMS噪声：0.75–1 mg，偏置±20–40 mg。
• 陀螺仪随机游走：4.712×10⁻⁶ rad/s²/√Hz。

四、卡尔曼滤波器设计

1. 状态方程设计

   • 状态向量：
   • 系统模型：
     四元数动力学方程描述姿态变化，陀螺仪零偏建模为随机游走过程。

2. 观测方程设计

   • 加速度计观测：重力方向与四元数预测姿态对比，用于俯仰角（Pitch）和横滚角（Roll）校正。
   • 磁力计观测：地磁场方向与预测航向角对比，用于Yaw角校正。

3. 非线性处理

   • 扩展卡尔曼滤波（EKF） ：对非线性模型进行一阶泰勒展开线性化。
   • 无迹卡尔曼滤波（UKF） ：通过Sigma点传播避免线性化误差，适用于强非线性系统。

---

五、算法实现案例

1. Matlab实现

   • 状态初始化：四元数初始化为单位四元数，零偏初始化为0。
   • 动态绘图：通过实时更新欧拉角（Pitch/Roll/Yaw）展示姿态变化。

2. 嵌入式系统优化

   • MPU9250数据融合：采用互补滤波预降噪，再输入EKF进行姿态解算。
   • ROS节点封装：将滤波后的IMU数据与视觉/激光雷达融合，提升SLAM精度。

---

六、挑战与解决方案

挑战	解决方案
传感器时间同步	FPGA硬件级时间戳对齐，置信区间划分实现毫秒级同步
磁力计动态干扰	抗磁干扰算法（如A9模块的动态磁场初始化）
计算资源限制	固定点运算优化，状态向量降维（如分离姿态与零偏估计）
非线性姿态表示	四元数替代欧拉角，避免万向节锁问题
动态环境适应性	自适应噪声协方差调整（如根据加速度计方差动态调整RR）

---

七、结论

卡尔曼滤波器在9轴IMU中通过多传感器数据融合，有效解决了单一传感器的局限性：

• 精度提升：静态精度可达0.1°，动态精度0.5°（A9模块）。
• 实时性：支持1125Hz数据率（ICM20948），满足无人机/机器人实时控制需求。
• 扩展性：与视觉/GNSS融合可构建更高精度的导航系统。

未来方向包括：基于深度学习的噪声建模、低功耗嵌入式优化，以及多模态传感器融合框架的标准化。

📚2 运行结果

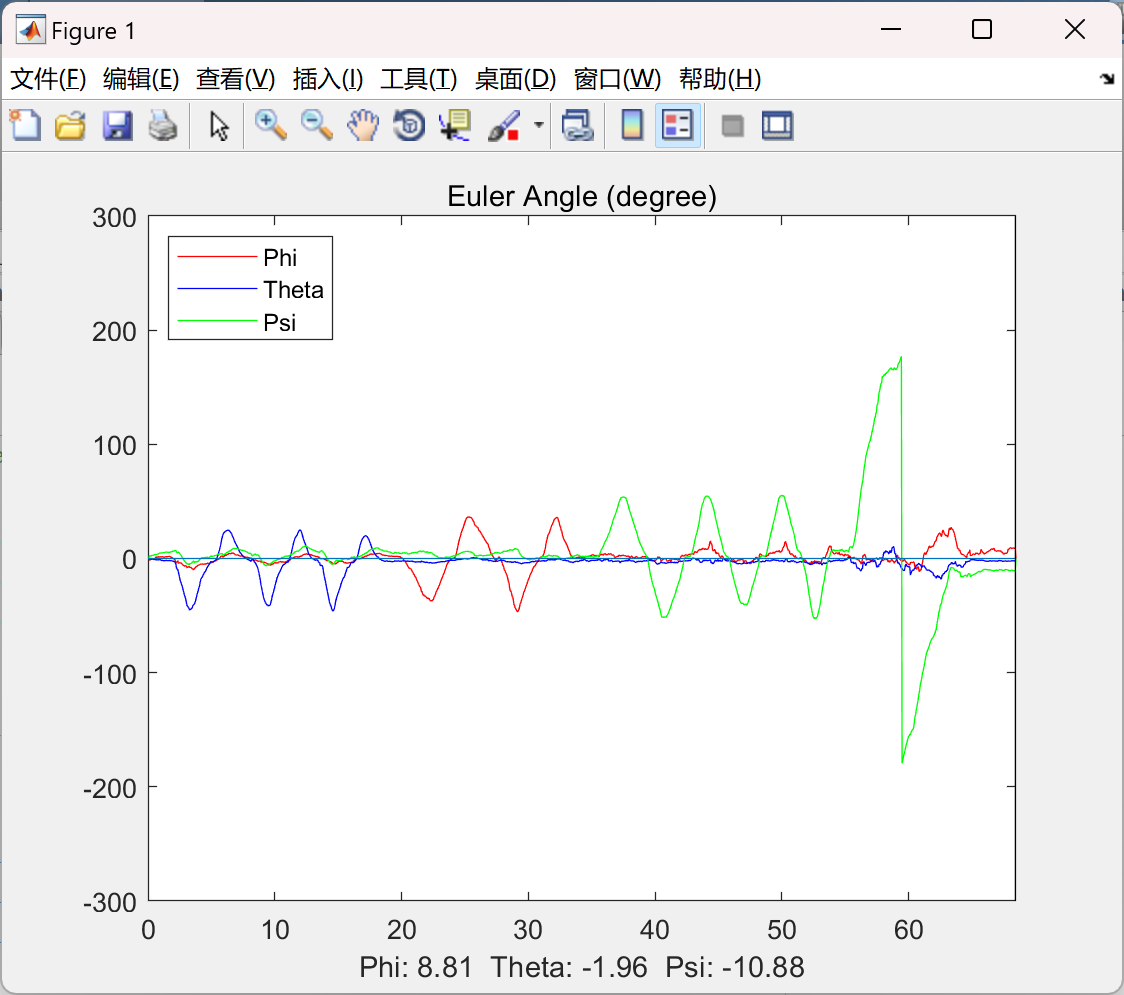
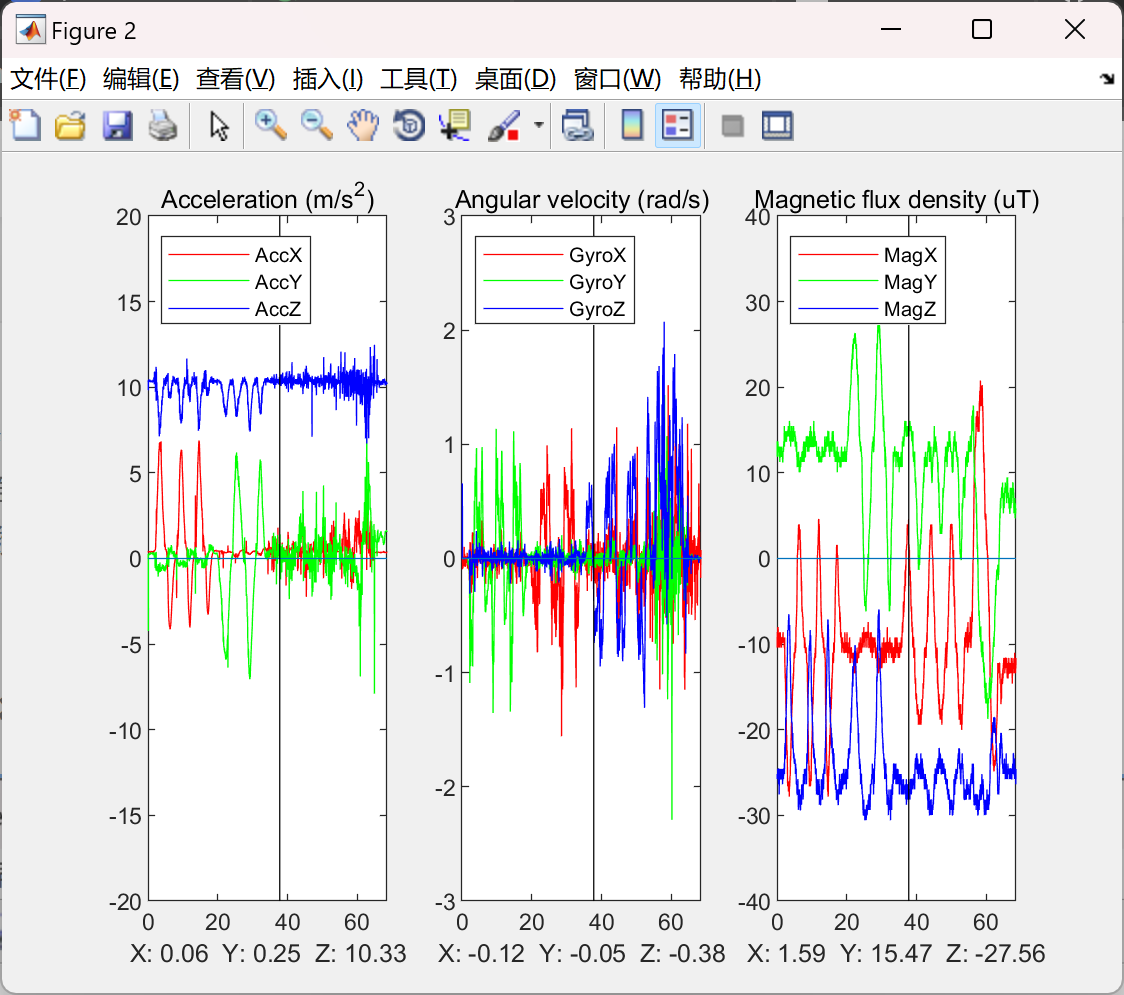
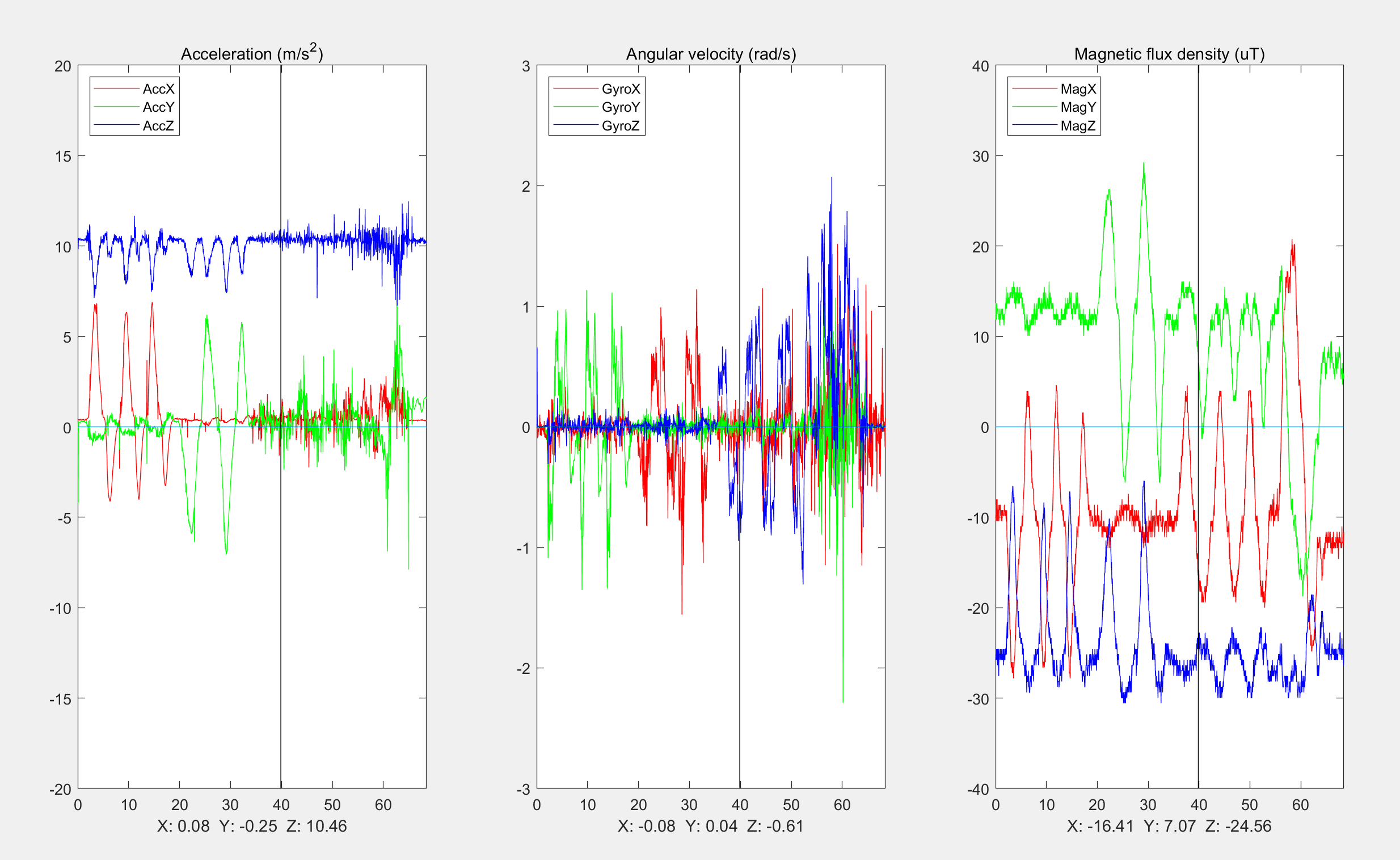
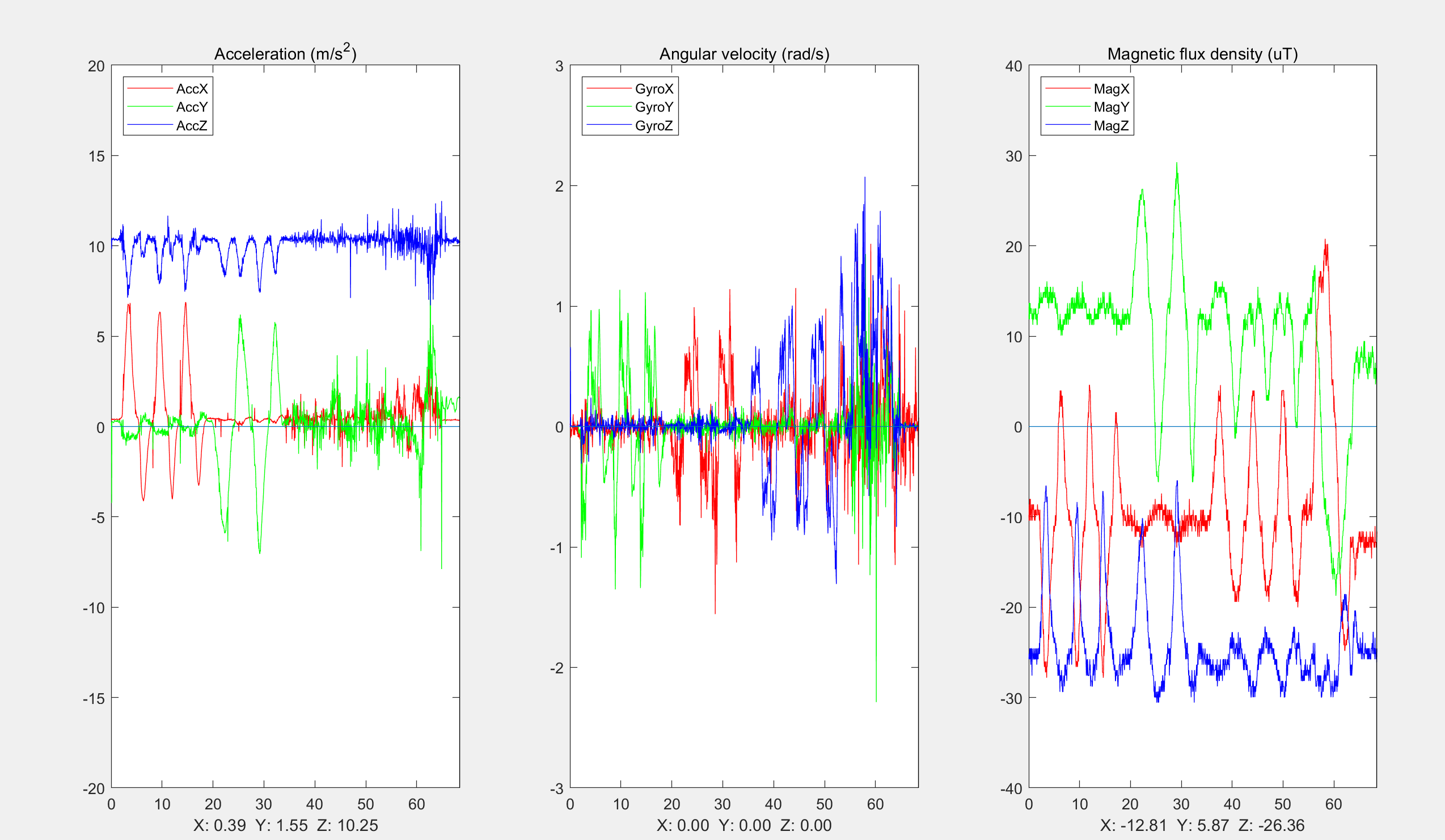
部分代码：

figure()
P1=plot(DATA_SI(10,:), PhiSaved, 'r');
hold on
P2=plot(DATA_SI(10,:), ThetaSaved, 'b');
P3=plot(DATA_SI(10,:), PsiSaved, 'g');
refline([0 0])
title('Euler Angle (degree)')
Timeline_1 = line('XData',x,'YData',y);
TimeValue_1= xlabel('');
legend([P1 P2 P3],{'Phi', 'Theta', 'Psi'},'Location','northwest','AutoUpdate','off');
axis([0 DATA_SI(10,Nsamples) -300 300])

figure()
subplot(1,3,1)
plot(DATA_SI(10,:),DATA_SI(1,:),'r',DATA_SI(10,:),DATA_SI(2,:),'g',DATA_SI(10,:),DATA_SI(3,:),'b');
refline([0 0])
title('Acceleration (m/s^2)');
Timeline_2 = line('XData',x,'YData',y);
TimeValue_2= xlabel('');
legend({'AccX', 'AccY', 'AccZ'},'Location','northwest','AutoUpdate','off');
axis([0 DATA_SI(10,Nsamples) -20 20])

subplot(1,3,2)
plot(DATA_SI(10,:),DATA_SI(4,:),'r',DATA_SI(10,:),DATA_SI(5,:),'g',DATA_SI(10,:),DATA_SI(6,:),'b');
refline([0 0])
title('Angular velocity (rad/s)')
Timeline_3 = line('XData',x,'YData',y);
TimeValue_3= xlabel('');
legend({'GyroX', 'GyroY', 'GyroZ'},'Location','northwest','AutoUpdate','off');
axis([0 DATA_SI(10,Nsamples) -3 3])

subplot(1,3,3)
plot(DATA_SI(10,:),DATA_SI(7,:),'r',DATA_SI(10,:),DATA_SI(8,:),'g',DATA_SI(10,:),DATA_SI(9,:),'b');
refline([0 0])
title('Magnetic flux density (uT)')
Timeline_4 = line('XData',x,'YData',y);
TimeValue_4= xlabel('');
legend({'MagX', 'MagY', 'MagZ'},'Location','northwest','AutoUpdate','off');
axis([0 DATA_SI(10,Nsamples) -40 40])

%% Graphical Plot & Dynamic Plot
%set IMU Object's vertex
Cuboid_1=[-2,-3,-0.5];
Cuboid_2=[2,-3,-0.5];
Cuboid_3=[2,3,-0.5];
Cuboid_4=[-2,3,-0.5];
Cuboid_5=[-2,-3,0.5];
Cuboid_6=[2,-3,0.5];
Cuboid_7=[2,3,0.5];
Cuboid_8=[-2,3,0.5];
Cuboid=[Cuboid_1; Cuboid_2; Cuboid_3; Cuboid_4; Cuboid_5; Cuboid_6; Cuboid_7; Cuboid_8];
% ?
fac = [1 2 6 5;2 3 7 6;3 4 8 7;4 1 5 8;1 2 3 4;5 6 7 8];
%Plot Object
figure()
view(3)
Obejct_IMU = patch('Faces', fac, 'Vertices', [0, 0, 0]);
Obejct_IMU.FaceColor = 'g';
axis([-5 5 -5 5 -5 5])
title('IMU state')
Realtime = xlabel(' ');
%Animate
for k=1:Nsamples-1
    %Rotation matrix for vertex
    Rz = [cosd(PsiSaved(k)) -sind(PsiSaved(k)) 0; sind(PsiSaved(k)) cosd(PsiSaved(k)) 0; 0 0 1];
    Ry = [cosd(ThetaSaved(k)) 0 sind(ThetaSaved(k)); 0 1 0; -sind(ThetaSaved(k)) 0 cosd(ThetaSaved(k))];
    Rx = [1 0 0; 0 cosd(PhiSaved(k)) -sind(PhiSaved(k)); 0 sind(PhiSaved(k)) cosd(PhiSaved(k))];
    dt=(DATA_SI(10,k+1)-DATA_SI(10,k));
for j=1:8

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]王晓初,李宾,刘玉县,等.一种基于改进卡尔曼滤波的姿态解算算法[J].科学技术与工程, 2019, 19(24):7.DOI:CNKI:SUN:KXJS.0.2019-24-071.

[2]蔡阳,胡杰.基于卡尔曼滤波和互补滤波的AHRS系统研究[J].电脑知识与技术:学术版, 2021.

[3]陆永杰.基于多传感器融合的室外室内连续定位系统研究[D].南京邮电大学[2024-05-09]. 

🌈4 Matlab代码、数据