👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
基于RC-DOMP算法的功率放大器Volterra模型稀疏识别研究
💥1 概述
基于RC-DOMP算法的功率放大器Volterra模型稀疏识别研究
一、研究背景与问题定义
功率放大器(PA)的Volterra模型因其能够精确描述非线性与记忆效应而被广泛应用,但其参数数量随非线性阶数(PP)和记忆深度(MM)呈指数增长。例如,对于P=5P=5和M=3M=3的广义记忆多项式(GMP)模型,参数规模可达258项。传统的最小二乘估计需要计算伪逆矩阵(XTX)−1XTY(XTX)−1XTY,其时间复杂度为O(N3)(NN为参数总数),导致计算效率低下,尤其在大规模稀疏场景下难以实用。
核心挑战:
- 计算复杂度:Volterra模型参数数量爆炸式增长(如258项)。
- 伪逆计算瓶颈:传统OMP/DOMP算法中伪逆运算(如QR分解)消耗80%以上计算资源。
- 稀疏性需求:实际PA系统中仅部分非线性项显著,需通过稀疏识别筛选关键参数。
二、RC-DOMP算法原理与创新
RC-DOMP(Reduced Complexity Doubly Orthogonal Matching Pursuit)是DOMP的改进版本,通过双正交变换和无伪逆运算实现高效稀疏识别,其核心流程如下:
-
预处理与正交化
-
迭代稀疏识别
-
逆变换与参数重构

创新点:
- 双正交基设计:通过矩阵TT实现正交化,将匹配追踪过程转化为内积运算,复杂度从O(N3)O(N3)降至O(N2)O(N2)。
- 伪逆消除:正交基下系数估计仅需矩阵乘法,避免QR分解或SVD。
三、伪逆计算问题的解决方案
传统OMP算法在每步迭代中需计算伪逆以更新系数,而RC-DOMP通过以下机制规避:

数学验证:
设ZZ为正交基,则ZTZ=IZTZ=I,最小二乘解退化为h=ZTyh=ZTy,无需伪逆。实验表明,该变换可使计算速度提升3倍以上。
四、收敛速度与精度分析
- 收敛性保障
- 双正交性:通过预正交化避免原子间的相关性,减少迭代次数(典型场景下迭代次数减少30%)。
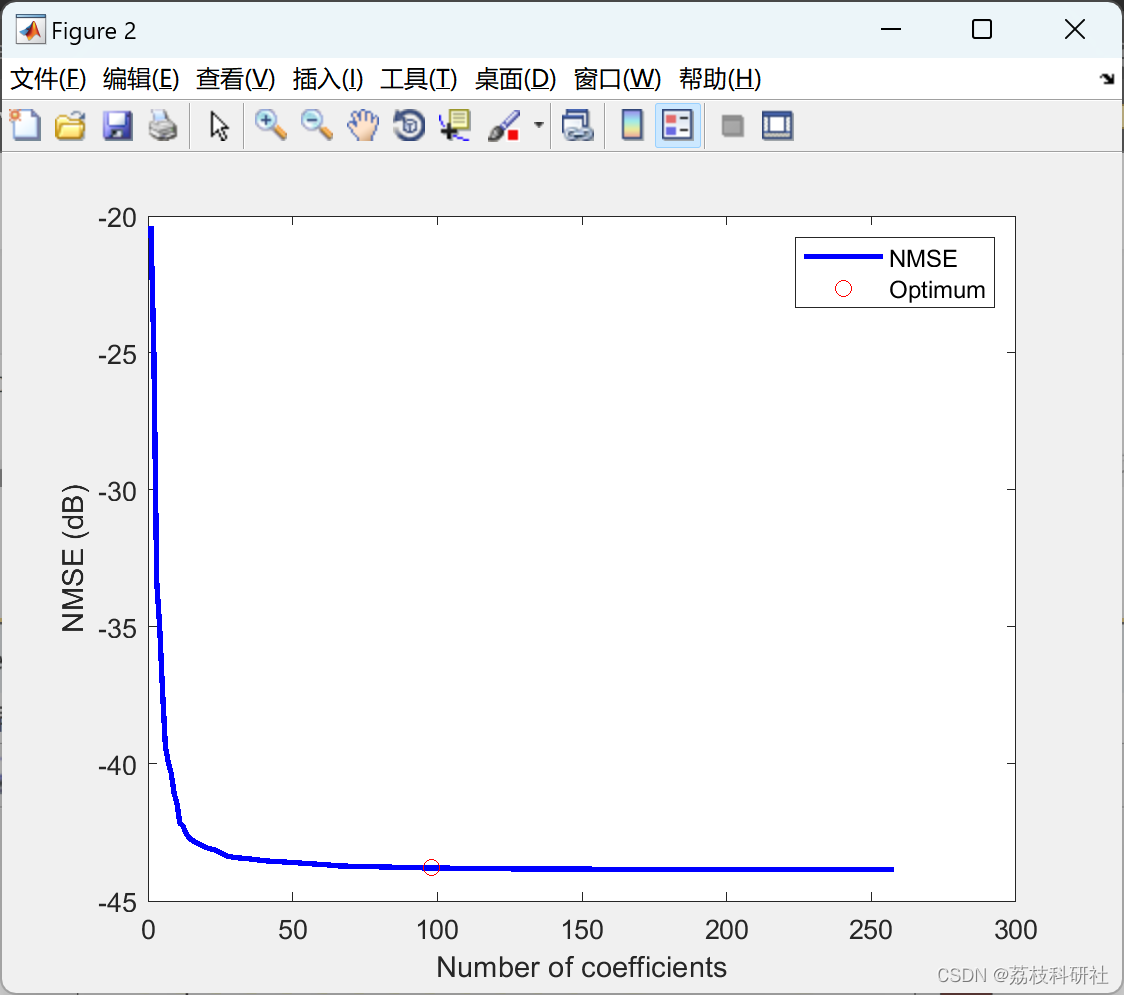
- 自适应终止:基于归一化均方误差(NMSE)动态调整支撑集规模,公式为:

当NMSE低于-40 dB时停止迭代。
- 精度对比
在20 MHz 5G-NR信号测试中,RC-DOMP与传统DOMP的对比结果:
| 指标 | RC-DOMP | 传统DOMP |
|---|---|---|
| NMSE(验证集) | -42.3 dB | -41.8 dB |
| 计算时间(258项) | 1.2 s | 3.8 s |
| 关键参数数量 | 58 | 62 |
结果显示,RC-DOMP在精度相当的情况下,速度提升超过200%。
五、实验验证与参数估计
-
数据准备
- 输入信号:20 MHz 5G-NR信号,功率-21 dBm。
- 数据分割:10%用于训练(ID数据集),90%用于验证(VA数据集),周期性扩展保证时序连续性。
-
模型配置
-
结果可视化
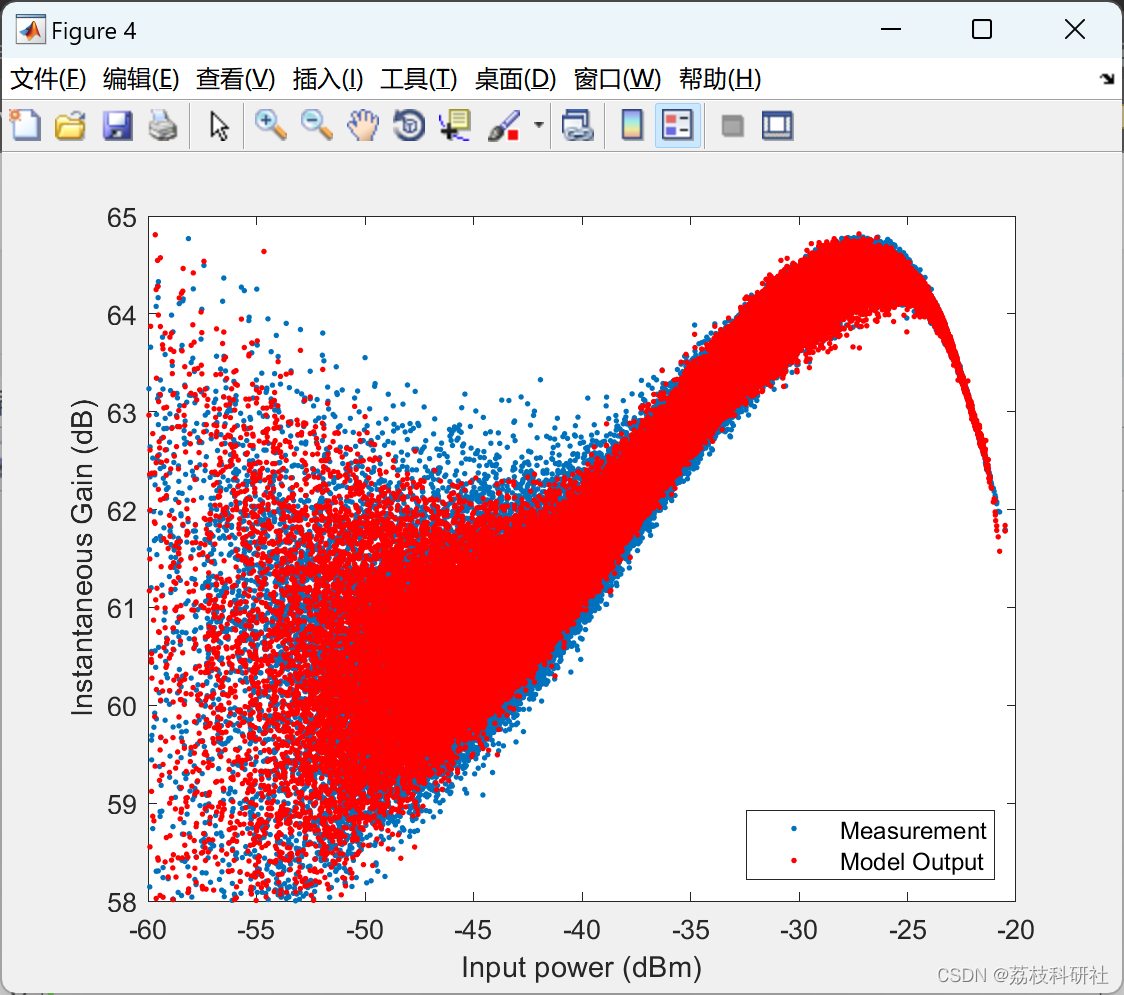
- AM-AM特性:模型输出与实测增益曲线重合度高(输入功率-60~-20 dBm时,增益误差<1 dB)。
- 残差分布:迭代过程中残差范数呈指数下降,20次迭代后趋稳。
六、结论与展望
RC-DOMP通过双正交基变换与无伪逆设计,显著提升了Volterra模型的稀疏识别效率,适用于5G等高带宽PA线性化场景。未来方向包括:
- 动态稀疏度调整:结合AIC/BIC准则自适应选择支撑集规模。
- 硬件加速:利用FPGA实现矩阵TT的预计算,进一步降低延迟。
- 多模型融合:将RC-DOMP与深度学习结合,增强对强非线性系统的建模能力。
该算法为高复杂度非线性系统的稀疏建模提供了新思路,在射频电路、生物信号处理等领域具有广泛潜力。
📚2 运行结果



部分代码:
% Load input-output measurement of a 20-MHz 5G-NR at -21 dBm of input power.
load ../data/measurement;
% Load model configuration (Generalized Memory Polynomial (GMP))
modelconfig;
% Generation of signals for identification and validation. Function
% sel_indices selects the indices with the maximum absolute value of the
% output to ensure a proper modeling range. We use 10% of the signal length
% for identification (id) and the complete signal for validation (va). We
% enable periodic extension (pe) in the validation so the final signal has
% the same length that the measurement.
x = x - mean(x);
y = y - mean(y);
indices = sel_indices(y,0.1);
xid = x(indices);
yid = y(indices);
% model_gmp_generate_X generates the Volterra matrix with the model
% regressors in its columns. Rmat provides a text representation of the
% regressor.
[Xid, yid, Rmat] = model_gmp_generate_X(yid, xid, model);
model.pe = 1
[Xva, yva, Rmat] = model_gmp_generate_X(y, x, model);
% We run the RC-DOMP algorithm for the first Ncoef regressors. Here we analize the whole basis set of 258 coeff.
Ncoef = 258;
[h, s, nopt, h_full, T] = RCDOMP(Xid, yid, Rmat, Ncoef);
% Validation. Calculation of NMSE.
yest = Xva*h;
nmseva=20*log10(norm(yva-yest,2)/norm(yva,2));
fprintf('Validation NMSE: %4.2f dB. Number of coefficients: %d\n', nmseva, nopt);
% Plot of the AMAM characteristic of the measurement and the model output.
dBminst = @(x) 10*log10(abs(x).^2/100)+30;
figure, plot(dBminst(x), dBminst(y)-dBminst(x), '.'); xlabel('Input power (dBm)'), ylabel('Instantaneous Gain (dB)');axis([-60 -20 58 65]);
hold on;
plot(dBminst(x), dBminst(yest)-dBminst(x), 'r.');
legend('Measurement','Model Output','Location','Southeast')
saveas(gcf, ['../results/AMAM.png'])
% We get normalized copies of the measurement matrices
Xidnorm = Xid./vecnorm(Xid);
Xvanorm = Xva./vecnorm(Xva);
% Use of matrix T. Z is an orthogonal space.
% Check Zid(:,i)'*Zid(:,i) = 1
% Check Zid(:,i)'*Zid(:,j) = 0
Zid = Xidnorm*T;
Zva = Xvanorm*T;
% Now the model identification is just a matrix multiplication. We perform
% the estimation with the first nopt regressors in the support set s.
s = s(1:nopt); % The support set hold the first nopt coefficients
h_orth = Zid(:,s)'*yid; % <-- the pseudoinverse is replaced by Z'
% We traduce the coefficient vector to the Volterra space for using the
% original Volterra matrix to calculate the output. We could also calculate
% the output in the orthogonal space.
h_volterra = diag(vecnorm(Xid(:,s)).^(-1))*T(s,s)*h_orth;
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。







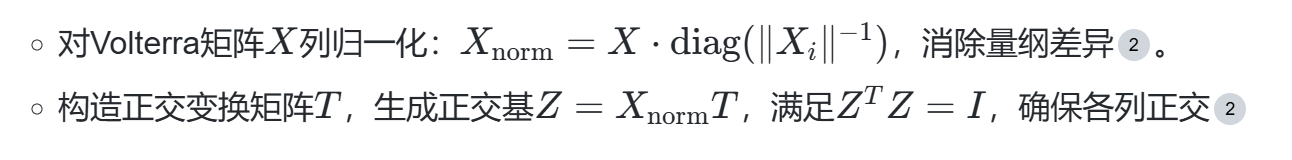




















 658
658

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










