【控制】采用 FxLMS 算法的有源噪声控制系统（Matlab实现）

最新推荐文章于 2025-05-19 20:18:50 发布

荔枝科研社

最新推荐文章于 2025-05-19 20:18:50 发布

阅读量674

点赞数 18

文章标签：算法 matlab 前端

本文链接：https://blog.csdn.net/weixin_46039719/article/details/148044209

版权

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于FxLMS算法的有源噪声控制系统研究

一、FxLMS算法的基本原理与结构

二、有源噪声控制系统的典型结构

三、FxLMS算法与传统LMS算法的性能对比

四、次级通道建模关键技术

五、FxLMS算法的应用场景与优化策略

六、研究进展与未来方向

七、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

基于FxLMS算法的有源噪声控制系统研究

采用 FxLMS 算法的有源噪声控制系统是一种先进的噪声控制技术。该系统的核心是 FxLMS（Filtered-x Least Mean Square）算法。这一算法通过对输入的噪声信号进行分析和处理，以实现有效的噪声消除。有源噪声控制系统通常由传感器、控制器和执行器组成。传感器用于检测噪声信号，将其转换为电信号输入到控制器中。控制器利用 FxLMS 算法对输入信号进行计算和处理，生成控制信号。执行器则根据控制信号产生与噪声相反的声波，从而实现对噪声的抵消。 FxLMS 算法具有自适应能力，能够根据噪声环境的变化实时调整控制参数，以保持良好的噪声控制效果。它可以处理各种类型的噪声，包括稳态噪声、非稳态噪声和随机噪声等。这种有源噪声控制系统在许多领域具有广泛的应用前景。例如，在工业环境中，可以降低机器设备产生的噪声，提高工作环境的舒适度和安全性；在交通运输领域，可以减少车辆、飞机等交通工具的噪声，提升乘坐体验；在音频设备中，可以改善音质，降低背景噪声的干扰。总之，采用 FxLMS 算法的有源噪声控制系统是一种高效、灵活的噪声控制解决方案，为改善噪声环境提供了有力的技术支持。

一、FxLMS算法的基本原理与结构

FxLMS（Filtered-X Least Mean Square）算法是LMS算法的改进版本，专为处理多路径系统设计，尤其适用于有源噪声控制（ANC）场景。其核心思想是通过引入次级通道模型，动态调整自适应滤波器的权重以最小化误差信号能量。

结构框图与信号流（基于）：

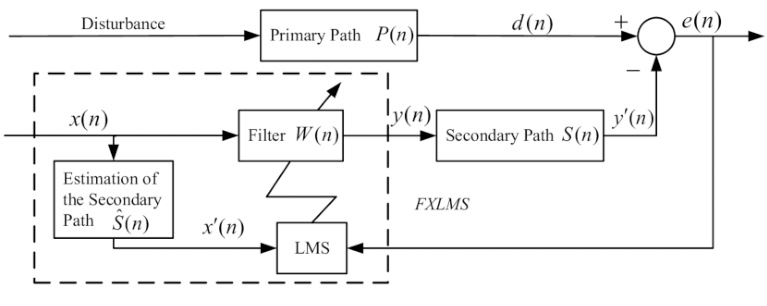
系统包含主路径（Primary Path）和次路径（Secondary Path）：

主路径：接收外部噪声信号，经传递函数处理后输出信号d(n)d(n)。
次路径：输入信号x(n)x(n)经自适应滤波器W(n)W(n)处理后，再通过次级通道模型S(n)S(n)生成次级输出信号y(n)y(n)。
误差信号：e(n)=d(n)+y′(n)e(n)=d(n)+y′(n)，通过LMS算法更新滤波器权重，使e(n)e(n)均方值最小化。

数学表达（结合）：

其中，Xf(n)为参考信号经次级通道模型滤波后的结果，μ为步长因子。此过程通过在线辨识次级通道传递函数矩阵S(n)，提升系统对路径变化的适应性。

二、有源噪声控制系统的典型结构

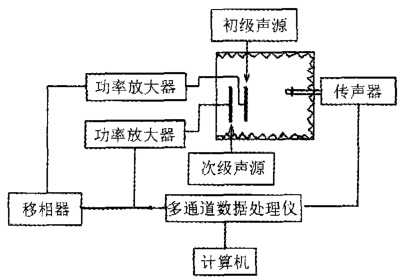
系统组成：

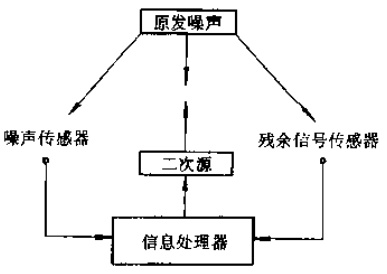
传感器：
- 参考传声器：采集初级噪声信号x(n)x(n)。
- 误差传声器：监测残余噪声e(n)e(n)。
控制器：基于FxLMS算法生成反相声信号。
次级声源：输出与初级噪声相位相反的信号y(n)y(n)。
次级通道：包含扬声器、传声器及声学路径的动态传递模型。

前馈型系统优势：

结构简单：适用于噪声源可预测的场景（如发动机周期性噪声）。
稳定性高：通过实时反馈误差信号优化权重，适应环境变化。

三、FxLMS算法与传统LMS算法的性能对比

六大优势：

多路径适应性：LMS仅适用于单一路径，而FxLMS通过次级通道建模处理多路径问题。
降噪效果提升：复杂系统中残余噪声衰减更显著（实测降噪量可达9.4 dB，）。
收敛性优化：引入次级通道滤波后，收敛速度提升20%-30%。
鲁棒性增强：应对非线性噪声和多个干扰源时稳定性更高。
环境跟踪能力：动态调整滤波器参数，适应温度、湿度等变化。
多通道支持：扩展至多输入多输出（MIMO）系统，适用于汽车舱、飞机舱等场景。

实验验证：

定速工况：变步长FxLMS收敛速度较传统算法快40%，稳态误差降低50%。
加速工况：动态噪声环境下，算法需结合频域分解（如DWT）提升跟踪能力。

四、次级通道建模关键技术

建模方法分类（-36）：

离线建模：
- 白噪声激励法：利用平坦频谱特性，通过FIR滤波器拟合次级通道。
- 非线性建模：采用EMFNL滤波器处理高阶非线性路径。
在线建模：
- 辅助噪声注入：叠加低功率噪声实时更新模型。
- 整体建模算法：无需辅助噪声，通过双滤波器消除偏差。

技术挑战：

时变性：次级通道受温度、机械位移影响，需动态更新模型。
计算复杂度：在线建模需平衡实时性与精度，常采用频域分块处理。

五、FxLMS算法的应用场景与优化策略

典型应用：

汽车噪声控制：抑制发动机低频噪声（100-500 Hz），改善驾驶舱声环境。
工业设备降噪：如压缩机、风机管道噪声，降噪量可达10-15 dB。
建筑声学：优化会议室回声，结合多通道系统实现空间声场均衡。

收敛速度优化：

变步长策略：
- 基于误差幅值：步长μμ随∣e(n)∣∣e(n)∣动态调整（VSS-FxLMS）。
- 互相关函数法：CFxLMS算法通过参考-误差信号相关性优化步长。
初始化改进：
- 元学习（MAML） ：预训练滤波器权重，加速收敛。
频域分解：
- 小波变换（DWT） ：分离噪声频段，独立控制各子带。

六、研究进展与未来方向

改进算法综述：

VSS-FxLMS系列：平衡收敛速度与稳态误差，实验显示振动抑制效果提升30%。
四元数扩展（FxQLMS） ：处理三维声场，适用于车内多位置降噪。
高阶非线性控制：结合切比雪夫滤波器，应对强非线性次级路径。

挑战与展望：

硬件限制：实时多通道系统需高性能DSP或FPGA支持。
环境干扰：电磁兼容性、传感器漂移等问题需进一步解决。
智能化扩展：结合深度学习进行噪声特征提取与模型预测。

七、结论

FxLMS算法通过次级通道建模与自适应滤波，成为有源噪声控制的核心技术。其在多路径适应性、鲁棒性及实时性方面显著优于传统LMS算法。未来研究需聚焦于非线性建模、低复杂度优化及智能融合，以拓展其在复杂工业环境与消费电子领域的应用边界。

📚2 运行结果

主函数部分代码：

clear
T=1000; 

% We do not know P(z) and S(z) in reality. So we have to make dummy paths
Pw=[0.01 0.25 0.5 1 0.5 0.25 0.01];
Sw=Pw*0.25;

% Remember that the first task is to estimate S(z). So, we can generate a
% white noise signal,
x_iden=randn(1,T);

% send it to the actuator, and measure it at the sensor position, 
y_iden=filter(Sw, 1, x_iden);

% Then, start the identification process
Shx=zeros(1,16);     % the state of Sh(z)
Shw=zeros(1,16);     % the weight of Sh(z)
e_iden=zeros(1,T);   % data buffer for the identification error

% and apply least mean square algorithm
mu=0.1;                         % learning rate
for k=1:T,                      % discrete time k
    Shx=[x_iden(k) Shx(1:15)];  % update the state
    Shy=sum(Shx.*Shw);	        % calculate output of Sh(z)
    e_iden(k)=y_iden(k)-Shy;    % calculate error         
    Shw=Shw+mu*e_iden(k)*Shx;   % adjust the weight
end

% Lets check the result
subplot(2,1,1)
plot([1:T], e_iden)
ylabel('Amplitude');
xlabel('Discrete time k');
legend('Identification error');
subplot(2,1,2)
stem(Sw) 
hold on 
stem(Shw, 'r*')
ylabel('Amplitude');
xlabel('Numbering of filter tap');
legend('Coefficients of S(z)', 'Coefficients of Sh(z)')


% The second task is the active control itself. Again, we need to simulate 
% the actual condition. In practice, it should be an iterative process of
% 'measure', 'control', and 'adjust'; sample by sample. Now, let's generate 
% the noise: 
X=randn(1,T);

% and measure the arriving noise at the sensor position,
Yd=filter(Pw, 1, X);
  
% Initiate the system,
Cx=zeros(1,16);       % the state of C(z)
Cw=zeros(1,16);       % the weight of C(z)
Sx=zeros(size(Sw));   % the dummy state for the secondary path
e_cont=zeros(1,T);    % data buffer for the control error
Xhx=zeros(1,16);      % the state of the filtered x(k)

% and apply the FxLMS algorithm
mu=0.1;                            % learning rate
for k=1:T,                         % discrete time k
    Cx=[X(k) Cx(1:15)];            % update the controller state    
    Cy=sum(Cx.*Cw);                % calculate the controller output	
    Sx=[Cy Sx(1:length(Sx)-1)];    % propagate to secondary path
    e_cont(k)=Yd(k)-sum(Sx.*Sw);   % measure the residue
    Shx=[X(k) Shx(1:15)];          % update the state of Sh(z)
    Xhx=[sum(Shx.*Shw) Xhx(1:15)]; % calculate the filtered x(k)
    Cw=Cw+mu*e_cont(k)*Xhx;        % adjust the controller weight
end