MPC---模型预测控制设计及基于CARLA的Python代码实现

汤姆_布利柏

已于 2024-04-28 16:05:37 修改

阅读量2k

点赞数 5

文章标签：自动驾驶算法

于 2023-11-14 21:59:39 首次发布

本文链接：https://blog.csdn.net/weixin_46072670/article/details/134320722

版权

1、MPC设计

　　MPC：通过模型来预测系统在某一未来时间段内的表现来进行优化控制。

　　MPC是典型的控制算法，能够处理自动驾驶中的横向控制问题。多用于数位控制，所以采用离散型的状态空间方程（连续方程离散化）。

$x_{k+1}=Ax_{k}+Bu_{k}$

　　下面的是输入u，上面的是输出y，参考值是r，k代表当下的时刻，k以前代表过去，k以后代表未来。在k时刻先测量或估计到了当前的状态 $x_{k}$ ，输出是 $y_{k}$ 。

　　MPC的设计分为三个步骤。

　　（1）获取k时刻的系统状态

　　第一步要做的是估计或测量当前的（在k时刻）系统状态，有的系统状态可以测量出来，但有的系统状态不能测量就需要用到估计的方法。

　　（2）算出最优的 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$

　　第二步是算出最优的 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$ 进行最优化控制。过程是在k时刻输入 $u_{k}$ ，系统就会基于状态方程和输出方程的模型输出表现 $y_{k}$ ，然后k+1时刻输入 $u_{k+1}$ ，系统就会基于状态方程和输出方程的模型输出表现 $y_{k+1}$ ，一直进行下去到n（n就是MPC每一次实施的步长）。从k时刻到k+n时刻的输入就是Control Horizon（控制区间），从k时刻到k+n时刻的输出就是Predictive Horizon（预测区间）。

　　因此，要想得到最优的控制 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$ ，设计代价函数：

$J=\sum_{k}^{k+n-1}(E_{k}^{T}QE_{k}+u_{k}^{T}Ru_{k})+E_{k+n}^{T}FE_{k+n}$

　　其中， $E_{k}$ 是k时刻输出 $y_{k}$ 与参考r的误差， $E_{k+n}$ 是最后时刻的输出 $y_{k+n}$ 与参考r的误差， $Q$ 、 $R$ 、 $F$ 是权重系数矩阵， $Q$ 和误差（系统状态）相关， $R$ 和输入有关， $F$ 和终止时刻的误差（系统状态）相关。

　　目标就是最小化代价函数J算出最优控制 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$ 。

　　（3）选取最优的 $u_{k}$

　　第二步k时刻计算得到最优控制 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$ ，但是实施的时候只选取 $u_{k}$ 作为k时刻的控制。因为我们预测的模型很难完美描述现实的系统，而且现实的系统可能会有扰动。就是如果在k时刻施加控制 $u_{k}$ ，系统输出的表现是 $y_{k}$ ，但是实际上可能有偏差而不是 $y_{k}$ 这个值。因此，只需在每一次计算使得代价函数最小的最优控制之后仅仅选取的值 $u_{k}$ 施加，而不需要 $u_{k+1}$ 、...、 $u_{k+n}$ 。的值。

　　当时间到k+1时刻以后就需要把整个的控制区间和预测区间向未来移动一个时刻，再次的进行一下第二步的计算，然后只需选取k+1时刻算出的最优控制 $u_{k+1}$ ，以此来持续进行。每次就把窗口、区间向未来移动一步，这个过程就称为Receding Horizon Control（滚动优化控制）。

2、MPC建模

　　MPC的重点是如何解出最优的控制 $u_{k}$ 、 $u_{k+1}$ 、...、 $u_{k+n}$ ，这里采用二次规划的解法。因此，构建二次规划的模型。

$y_{k}=x_{k}$

$r=\vec{0}$

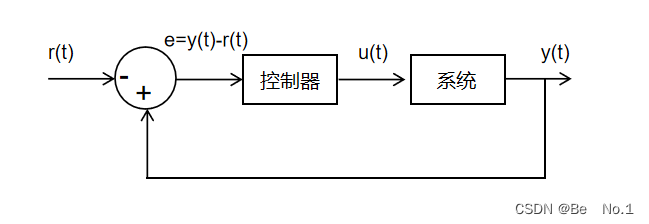
2.1、无常数项的系统状态空间方程

$x_{k+1}=Ax_{k}+Bu_{k}$

　　对于上述状态空间方程、输出方程， $x_{k}^{T}=\begin{bmatrix} x_{1} & x_{2} & ...& x_{n} \end{bmatrix}$ 是m×1的状态变量， $u_{k}^{T}=\begin{bmatrix} u_{1} & u_{2} & ...& u_{n} \end{bmatrix}$ 是p×1的输入向量。矩阵A是m×m大小，矩阵B是m×p大小。注意这里的矩阵A和B是离散化之后的而不是图上标注的（如何离散化可以查看自动驾驶控制算法---求解误差微分方程）。

　　在k时刻预测的k时刻、k+1时刻、...、k+n-1时刻的系统的控制变量（输入向量），在k时刻预测的k时刻、k+1时刻、...、k+n时刻的系统的状态变量、输出变量，以及误差：

$U_{k}=\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+n-1|k} \end{bmatrix}$ , $X_{k}=\begin{bmatrix} x_{k|k}\\ x_{k+1|k}\\ x_{k+2|k}\\ ...\\ x_{k+n|k} \end{bmatrix}$ ， $Y_{k}=X_{k}=\begin{bmatrix} x_{k|k}\\ x_{k+1|k}\\ x_{k+2|k}\\ ...\\ x_{k+n|k} \end{bmatrix}$ ， $E=Y_{k}-r=X_{k}=\begin{bmatrix} x_{k|k}\\ x_{k+1|k}\\ x_{k+2|k}\\ ...\\ x_{k+n|k} \end{bmatrix}$

　　其中 $U_{k}$ 是np×1大小的列向量， $X_{k}$ 、 $Y_{k}$ 和 $E$ 是(n+1)m×1大小的列向量。

　　　　代价函数（误差加权和+输入加权和+终端误差）：

$J=\sum_{i=0}^{n-1}(x_{k+i|k}^{T}Qx_{k+i|k}+u_{k+i|k}^{T}Ru_{k+i|k})+x_{k+n|k}^{T}Fx_{k+n|k}$

2.1.1、优化代价函数表达式

　　代价函数写成矩阵形式：

$J=\begin{bmatrix} x_{k|k}\\ x_{k+1|k}\\ x_{k+2|k}\\ ...\\ x_{k+n|k} \end{bmatrix}^{T}\begin{bmatrix} Q & 0 & 0 &... &0 \\ 0 & Q &0 &... &0 \\ 0& 0 & Q &... &0 \\ ...& ...& ... & ...& ...\\ 0& 0 &0 & ... &F \end{bmatrix}\begin{bmatrix} x_{k|k}\\ x_{k+1|k}\\ x_{k+2|k}\\ ...\\ x_{k+n|k} \end{bmatrix}+$

$\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+n-1|k} \end{bmatrix}^{T}\begin{bmatrix} R & 0&0 & ... & 0\\ 0& R& 0& ... &0 \\ 0 &0 &R &... &0 \\ ...& ... &... &... & ...\\ 0&0 &0 &... &R \end{bmatrix}\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+n-1|k} \end{bmatrix}$

$={X_{k}}^{T}\bar{Q}X_{k}+U{_{k}}^{T}\bar{R}U_{k}$

　　其中 $\bar{Q}$ 是(n+1)m×(n+1)m大小的矩阵， $\bar{R}$ 是np×np大小的矩阵。

　　由 $x_{k+1}=Ax_{k}+Bu_{k}$ 的关系及 $x_{k|k}=x_{k}$ 可得到：

$X_{k}=\begin{bmatrix} I\\ A\\ A^{2}\\ ...\\ A^{n} \end{bmatrix}x_{k}+\begin{bmatrix} 0 & 0 &... &0 \\ B & 0 & ... & 0\\ AB& B &... &0 \\ ...& ... & ... & ...\\ A^{n-1}B& A^{n-2}B& ... & B \end{bmatrix}\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+n-1|k} \end{bmatrix}$

$=Mx_{k}+CU_{k}$

　　其中 $M$ 是(n+1)m×m大小的矩阵， $C$ 是(n+1)m×np大小的矩阵， $X_{k}$ 是(n+1)m×1大小的列向量。

　　将上述公式代入代价函数：

$J={X_{k}}^{T}\bar{Q}X_{k}+U{_{k}}^{T}\bar{R}U_{k}=(Mx_{k}+CU_{k})^{T}\bar{Q}(Mx_{k}+CU_{k})+U{_{k}}^{T}\bar{R}U_{k}$

$J=x{_{k}}^{T}M^{T}\bar{Q}Mx_{k}+x{_{k}}^{T}M^{T}\bar{Q}CU_{k}+{U_{k}}^{T}C^{T}\bar{Q}Mx_{k}+$

${U_{k}}^{T}C^{T}\bar{Q}CU_{k}+{U_{k}}^{T}\bar{R}U_{k}$

$x_{k}$ ：m×1 $X_{k}$ ：(n+1)m×1 $U_{k}$ ：np×1

$M$ ：(n+1)m×m $C$ ：(n+1)m×np $\bar{Q}$ ：(n+1)m×(n+1)m

$\bar{R}$ ：np×np

　　代价函数J是一个数，J的第一项 $x{_{k}}^{T}M^{T}\bar{Q}Mx_{k}$ 、第四项 ${U_{k}}^{T}C^{T}\bar{Q}CU_{k}$ 和第五项 ${U_{k}}^{T}\bar{R}U_{k}$ 都是一个数。而且J的第二项 $x{_{k}}^{T}M^{T}\bar{Q}CU_{k}$ 和第三项 ${U_{k}}^{T}C^{T}\bar{Q}Mx_{k}$ 互为转置关系，因此：

$x{_{k}}^{T}M^{T}\bar{Q}CU_{k}={U_{k}}^{T}C^{T}\bar{Q}Mx_{k}$

　　那么代价函数：

$J=x{_{k}}^{T}Gx_{k}+2x{_{k}}^{T}EU_{k}+{U_{k}}^{T}HU_{k}$

　　其中 $G=M^{T}\bar{Q}M$ 是m×m大小的矩阵， $E=M^{T}\bar{Q}C$ 是m×np大小的矩阵， $H=C^{T}\bar{Q}C+\bar{R}$ 是np×np大小的矩阵。

　　因为 $x_{k}$ 是已知的数， $M$ 、 $\bar{Q}$ 是已知的矩阵，因此J也可以写为：

$J=2x{_{k}}^{T}EU_{k}+{U_{k}}^{T}HU_{k}$

　　再令 $E_{end}=(2x{_{k}}^{T}E)^{T}=2E^{T}x_{k}=2C^{T}\bar{Q}Mx_{k}$ 是np×1大小的矩阵， $H_{end}=2H=2(C^{T}\bar{Q}C+\bar{R})$ 是np×np大小的矩阵，那么符合二次规划形式的代价函数J如下：

$J=E{_{end}}^{T}U_{k}+\frac{1}{2}{U_{k}}^{T}H_{end}U_{k}$

　　　不等式约束是：

$-1<U_{k}<1$

2.2、带有常数项的系统状态空间方程

$x_{k+1}=Ax_{k}+Bu_{k}+C_{r}$

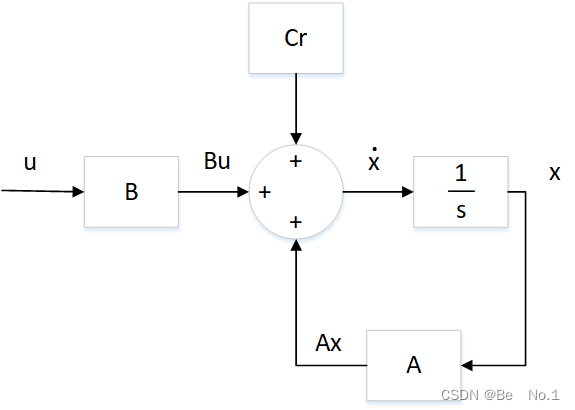
　　对于上述状态空间方程，矩阵 $C_{r}$ 是m×1大小。注意这里的矩阵A、矩阵B和矩阵 $C_{r}$ 均是是离散化之后的而不是图上标注的（如何离散化可以查看自动驾驶控制算法---求解误差微分方程）。

2.2.1、优化代价函数表达式

　　代价函数写成矩阵形式：

$J={X_{k}}^{T}\bar{Q}X_{k}+U{_{k}}^{T}\bar{R}U_{k}$

　　其中 $\bar{Q}$ 是(n+1)m×(n+1)m大小的矩阵， $\bar{R}$ 是np×np大小的矩阵。

　　变化的是 $X_{k}$ ：

$\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+n-1|k} \end{bmatrix}+\begin{bmatrix} 0\\ I\\ A+I\\ ...\\ A^{n-1}+A^{n-2}+...+I \end{bmatrix}C_{r}$

$=Mx_{k}+CU_{k}+C_{c}$

　　其中 $M$ 是(n+1)m×m大小的矩阵， $C$ 是(n+1)m×np大小的矩阵， $C_{c}$ 是(n+1)m×1大小的列向量， $X_{k}$ 是(n+1)m×1大小的列向量。

　　将上述公式代入代价函数：

$J={X_{k}}^{T}\bar{Q}X_{k}+U{_{k}}^{T}\bar{R}U_{k}$

$=(Mx_{k}+CU_{k}+C_{c})^{T}\bar{Q}(Mx_{k}+CU_{k}+C_{c})+U{_{k}}^{T}\bar{R}U_{k}$

$=x{_{k}}^{T}M^{T}\bar{Q}Mx_{k}+x{_{k}}^{T}M^{T}\bar{Q}CU_{k}+x{_{k}}^{T}M^{T}\bar{Q}C_{c}+$

${U_{k}}^{T}C^{T}\bar{Q}Mx_{k}+{U_{k}}^{T}C^{T}\bar{Q}CU_{k}+{U_{k}}^{T}C^{T}\bar{Q}C_{c}+$

$C{_{c}}^{T}\bar{Q}Mx_{k}+C{_{c}}^{T}\bar{Q}CU_{k}+C{_{c}}^{T}\bar{Q}C_{c}+{U_{k}}^{T}\bar{R}U_{k}$

$x_{k}$ ：m×1 $X_{k}$ ：(n+1)m×1 $U_{k}$ ：np×1

$M$ ：(n+1)m×m $C$ ：(n+1)m×np $C_{c}$ ：(n+1)m×1

$\bar{Q}$ ：(n+1)m×(n+1)m $\bar{R}$ ：np×np

　　代价函数J是一个数，J的每一项也都是一个数。而且J的第二项和第四项互为转置关系，第三项和第七项互为转置关系，第六项和第八项互为转置关系，因此：

$J=x{_{k}}^{T}Gx_{k}+2EU_{k}+{U_{k}}^{T}HU_{k}+2x{_{k}}^{T}M^{T}\bar{Q}C_{c}+C{_{c}}^{T}\bar{Q}C_{c}$

　　其中 $G=M^{T}\bar{Q}M$ 是m×m大小的矩阵， $E=x{_{k}}^{T}M^{T}\bar{Q}C+C{_{c}}^{T}\bar{Q}C$ 是1×np大小的矩阵， $H=C^{T}\bar{Q}C+\bar{R}$ 是np×np大小的矩阵。

　　因为 $x_{k}$ 是已知的数， $M$ 、 $\bar{Q}$ 、 $C_{c}$ 是已知的矩阵，因此J也可以写为：

$J=2EU_{k}+{U_{k}}^{T}HU_{k}$

　　再令 $E_{end}=2E^{T}=2(C^{T}\bar{Q}C_{c}+C^{T}\bar{Q}Mx_{k})$ 是np×1大小的矩阵， $H_{end}=2H=2(C^{T}\bar{Q}C+\bar{R})$ 是np×np大小的矩阵，那么符合二次规划形式的代价函数J如下：

$J=E{_{end}}^{T}U_{k}+\frac{1}{2}{U_{k}}^{T}H_{end}U_{k}$

　　　不等式约束是：

$-1<U_{k}<1$

2.3、解释预测区间(n)和控制区间(d)

　　以上的推导中，预测区间和控制区间一样长，控制是从 $u_{k|k}$ 到 $u_{k+n-1|k}$ （d=n步），预测是从 $y_{k+1|k}$ 到 $y_{k+n|k}$ （n步）。如果把 $y_{k|k}$ 算上的话，那么预测区间比控制区间多一步（n+1步），即使这样n依然等于d。

　　如果预测区间(n)不等于控制区间(d)，即假设n > d。那么相应矩阵的维度会发生变化。

$U_{k}=\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+d-1|k} \end{bmatrix}$

　　 $U_{k}$ 是dp×1大小的列向量。

　　代价函数（误差加权和+输入加权和+终端误差）：

$J=\sum_{i=0}^{n-1}(x_{k+i|k}^{T}Qx_{k+i|k})+\sum_{i=0}^{d-1}(u_{k+i|k}^{T}Ru_{k+i|k})+x_{k+n|k}^{T}Fx_{k+n|k}$

$\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+d-1|k} \end{bmatrix}^{T}\begin{bmatrix} R & 0&0 & ... & 0\\ 0& R& 0& ... &0 \\ 0 &0 &R &... &0 \\ ...& ... &... &... & ...\\ 0&0 &0 &... &R \end{bmatrix}\begin{bmatrix} u_{k|k}\\ u_{k+1|k}\\ u_{k+2|k}\\ ...\\ u_{k+d-1|k} \end{bmatrix}$

$={X_{k}}^{T}\bar{Q}X_{k}+U{_{k}}^{T}\bar{R}U_{k}$

　　其中 $\bar{Q}$ 是(n+1)m×(n+1)m大小的矩阵， $\bar{R}$ 是dp×dp大小的矩阵。

$=Mx_{k}+CU_{k}$

　　其中 $M$ 是(n+1)m×m大小的矩阵， $C$ 是(n+1)m×dp大小的矩阵， $X_{k}$ 是(n+1)m×1大小的列向量。

　　若d = 2，那么 $C$ 是(n+1)m×2p大小的矩阵：

$C=\begin{bmatrix} 0 & 0 \\ B & 0 \\ AB& B \\ ...& ... \\ A^{n-1}B& A^{n-2}B \end{bmatrix}$

　　对于无常数项的系统状态空间方程的推出的代价函数：

$J=E{_{end}}^{T}U_{k}+\frac{1}{2}{U_{k}}^{T}H_{end}U_{k}$

　　其中 $E_{end}2C^{T}\bar{Q}Mx_{k}$ 是dp×1大小的矩阵， $H_{end}=2(C^{T}\bar{Q}C+\bar{R})$ 是dp×dp大小的矩阵。

　　对于带有常数项的系统状态空间方程的推出的代价函数：

$J=E{_{end}}^{T}U_{k}+\frac{1}{2}{U_{k}}^{T}H_{end}U_{k}$

　　其中 $E_{end}=2(C^{T}\bar{Q}C_{c}+C^{T}\bar{Q}Mx_{k})$ 是np×1大小的矩阵， $H_{end}=2(C^{T}\bar{Q}C+\bar{R})$ 是np×np大小的矩阵。

最终找到了MPC对应的二次规划的代价函数形式， $x_{k}$ 是系统状态变量的初始状态（已知），J只与控制 $U_{k}$ 有关。然后求解使得代价函数J最小的控制 $U_{k}$ （可以用求解二次规划算法求解），取向量 $U_{k}$ 的k时刻预测的u就是使得误差渐渐趋于0的最优控制。

3、结合自动驾驶问题的基于MPC控制代码实现

　　MPC用于自动驾驶控制的横向控制。

　　1、导入库文件

import numpy as np
import math
import carla
import cvxopt
from collections import deque

　　2、初始化信息（车的位置信息、车的参数信息、主车变量、主车 $V_{x}$ 、规划出的信息、预测区间、控制区间、矩阵A、矩阵B、矩阵C、误差等）

class Lateral_MPC_controller(object):    #横向控制
    def __init__(self, ego_vehicle, vehicle_para, pathway_xy_theta_kappa):
        """
        self.vehicle_para = (a, b, Cf, Cr, m, Iz)
        a，b：前后轮中心距离车质心的距离
        CF, Cr：前后轮的侧偏刚度（按负的处理，apollo按正的处理）
        m：车的质量
        Iz：车的转动惯量
        """

        self.vehicle_para = vehicle_para
        self.vehicle_state = None  # self.vehicle_state = (x, y, fai, vy, fai_dao)存储车的位置信息
        self.vehicle = ego_vehicle  # ego_vehicle是carla中的主车
        self.vehicle_vx = 0   # ego_vehicle的车辆速度在车轴纵向方向的分量
        self.target_path = pathway_xy_theta_kappa  # 规划出的信息集(x_m, y_m, theta_m, k_m)
        self.n = 6  # 预测区间
        self.d = 3  # 控制区间
        self.m = 4  # 状态变量x有四个分量
        self.p = 1  # 控制输入u有一个分量
        # 根据误差微分方程来写A、B、C
        self.A = np.zeros(shape=(self.m, self.m), dtype="float64")
        self.B = np.zeros(shape=(self.m, self.p), dtype="float64")
        self.C = np.zeros(shape=(self.m, self.p), dtype="float64")
        self.A_bar = None  # 离散化的A矩阵
        self.B_bar = None  # 离散化的B矩阵
        self.C_bar = None  # 离散化的C矩阵
        self.k_r = None    # 投影点曲率
        self.err = None    # 车的信息和规划的信息的误差即状态变量
        self.min_index = 0

        self.x_pre = 0        # 预测点x
        self.y_pre = 0        # 预测点y
        self.fai_pre = 0      # 预测点fai
        self.fai_dao_pre = 0  # 预测点fai_dao
        self.vx_pre = 0       # 预测点vx
        self.vy_pre = 0       # 预测点vy

        self.x_r = 0       # 投影点x
        self.y_r = 0       # 投影点y
        self.theta_r = 0   # 投影点θ

　　3、获取车辆的位置和状态信息（位置（x，y）、车身横摆角φ、速度向量、航向角、质心侧偏角β、角速度 $\dot{\phi }$ 、vx以及vy）

    def vehicle_info(self):
        """
        函数：获取车辆的位置和状态信息
        return: None
        """

        vehicle_location = self.vehicle.get_location()  # self.vehicle.get_location()的格式：Location(x=70.000000, y=200.000000, z=1.942856)
        x, y = vehicle_location.x, vehicle_location.y  # 70.0   200.0
        fai = self.vehicle.get_transform().rotation.yaw * (math.pi / 180)  # 车身横摆角φ即车轴纵向和x轴的夹角，结果转成弧度制：79*π/180
        v = self.vehicle.get_velocity()  # self.vehicle.get_velocity()的格式：Vector3D(x=0.000000, y=0.000000, z=-0.194462)，航向角是车速v的方向与x轴夹角（=质心侧偏角β+车身横摆角φ）即arctan(v.y/v.x)
        v_length = math.sqrt(v.x * v.x + v.y * v.y + v.z * v.z)  # 速度大小
        beta = (math.atan2(v.y, v.x) - fai)  # 质心侧偏角β，车速和车轴纵向之间的夹角
        vx = v_length * math.cos(beta)  # 车速在车身坐标系下x轴(即纵向)的分量
        vy = v_length * math.sin(beta)  # 车速在车身坐标系下y轴(即横向)的分量
        '''
        当Vx的绝对值小于某一个值时，会导致矩阵H出现秩为1的情况导致二次规划无法求解，因此处理一下。
        '''
        if abs(vx) < 0.005 and vx >= 0:
            vx = 0.005
        if abs(vx) < 0.005 and vx < 0:
            vx = -0.005
        fai_dao = self.vehicle.get_angular_velocity().z * (math.pi / 180) # 角速度 self.vehicle.get_angular_velocity()的格式：Vector3D(x=0.000000, y=0.000000, z=0.000000)
        self.vehicle_state = (x, y, fai, vy, fai_dao)  # 得到车的位置和状态信息
        self.vehicle_vx = vx  # 得到ego_vehicle的车辆速度在纵向方向的分量

　　4、计算k时刻横向控制的误差err（即状态空间方程的 $x_{k}$ ）以及曲率 $k_r$

    def cal_err_k_r(self, ts=0.1):
        """
        函数：计算预测点和规划点的误差err
        ts:预测的时间
        self.target_path:规划模块输出的轨迹
        [(x_m1, y_m1, theta_m1, k_m1),
         (x_m2, y_m2, theta_m2, k_m2),
         ...
         (x_mn, y_mn, theta_mn, k_mn)]
        x_r, y_r:直角坐标系下位置
        theta_r:速度方向与x轴夹角
        k_r:规划点的曲率
        self.vehicle_state: 车辆当前位置(x, y, fai, vy, fai_dao)
        x,y:车辆当前的的实际位置
        fai:航向角即车轴和x轴的夹角
        fai_dao:fai对时间的导数即角速度
        vx:车的质心速度在车轴(纵向)方向的分量
        vy:车的质心速度在垂直车轴(横向)方向的分量
        return: None
        """

        vx = self.vehicle_vx
        x, y, fai, vy, fai_dao = self.vehicle_state

        # 预测模块计算预测点信息(因为算法具有滞后性)
        self.x_pre = x + vx * ts * math.cos(fai) - vy * ts * math.sin(fai)
        self.y_pre = y + vy * ts * math.cos(fai) + vx * ts * math.sin(fai)
        self.fai_pre = fai + fai_dao * ts
        self.fai_dao_pre = fai_dao
        self.vx_pre = vx
        self.vy_pre = vy

        # 1、找匹配点
        path_length = len(self.target_path)
        min_d = 1000
        for i in range(self.min_index, min(self.min_index + 50, path_length)):  # 向前搜索50个点
            d = (self.target_path[i][0] - x) ** 2 + (self.target_path[i][1] - y) ** 2
            if d < min_d:
                min_d = d
                self.min_index = i
        min_index = self.min_index

        # 2、计算自然坐标系下规划点的轴向向量tor和法向量n
        tor = np.array([math.cos(self.target_path[min_index][2]), math.sin(self.target_path[min_index][2])])
        n = np.array([-math.sin(self.target_path[min_index][2]), math.cos(self.target_path[min_index][2])])

        # 3、计算匹配点指向车位置的向量d_err
        d_err = np.array([x - self.target_path[min_index][0], y - self.target_path[min_index][1]])

        # 4、计算横向距离误差ed, 纵向距离误差es
        ed = np.dot(n, d_err)
        es = np.dot(tor, d_err)

        # 5、获取投影点坐标(x_r,y_r)
        self.x_r, self.y_r = np.array([self.target_path[min_index][0], self.target_path[min_index][1]]) + es * tor

        # 6、计算theta_r
        self.theta_r = self.target_path[min_index][2] + self.target_path[min_index][3] * es  # (按投影点的theta_m)
        # self.theta_r = self._target_path[min_index][2]  # apollo的方案(按匹配点的theta_m)

        # 7、计算投影点的曲率k_r，近似等于匹配点的曲率k_m
        self.k_r = self.target_path[min_index][3]

        # 8、计算ed的导数ed_dao
        ed_dao = self.vy_pre * math.cos(fai - self.theta_r) + vx * math.sin(fai - self.theta_r)

        # 9、计算e_fai
        e_fai = math.sin(fai - self.theta_r)
        # e_fai = fai - theta_r

        # 10、计算投影点速度(s的导数)s_dao
        s_dao = (vx * math.cos(fai - self.theta_r) - vy * math.sin(fai - self.theta_r)) / (1 - self.k_r * ed)

        # 11、计算e_fai的导数e_fai_dao
        e_fai_dao = fai_dao - self.k_r * s_dao

        self.err = (ed, ed_dao, e_fai, e_fai_dao)

　　5、计算矩阵A、B、C（根据状态空间方程代入车辆参数、vx），并计算离散化矩阵 $\bar{A}$ 、 $\bar{B}$ 、 $\bar{C}$

　　系统的状态空间方程：

$\begin{pmatrix} \dot{e_{d}}\\ \ddot{e_{d}}\\ \dot{e_{\varphi }}\\ \ddot{e_{\varphi }} \end{pmatrix}=\begin{pmatrix} 0 & 1 & 0 & 0\\ 0 & \frac{C_{\alpha f}+C_{\alpha r}}{mv_{x}} & -\frac{C_{\alpha f}+C_{\alpha r}}{m} & \frac{aC_{\alpha f}-bC_{\alpha r}}{mv_{x}}\\ 0 & 0 & 0 & 1\\ 0 & \frac{aC_{\alpha f}-bC_{\alpha r}}{Iv_{x}} & -\frac{aC_{\alpha f}-bC_{\alpha r}}{I} & \frac{a^{2}C_{\alpha f}+b^{2}C_{\alpha r}}{Iv_{x}} \end{pmatrix}\begin{pmatrix} e_{d}\\ \dot{e_{d}}\\ e_{\varphi }\\ \dot{e_{\varphi }} \end{pmatrix}+$

$\begin{pmatrix} 0\\ -\frac{C_{\alpha f}}{m}\\ 0\\ -a\frac{C_{\alpha f}}{I} \end{pmatrix}\delta +\begin{pmatrix} 0\\ \frac{aC_{\alpha f}-bC_{\alpha r}}{mv_{x}}-v_{x}\\ 0\\ \frac{a^{2}C_{\alpha f}+b^{2}C_{\alpha r}}{Iv_{x}} \end{pmatrix}\dot{\theta _{r}}$

$\dot{e_{rr}} = Ae_{rr} + Bu + C\dot{\theta _{r}}$

　　计算 $A$ 、 $B$ 、 $C$ 、 $\bar{A}$ 、 $\bar{B}$ 、 $\bar{C}$ 矩阵：

    def cal_A_B_C_and_discretion(self):
        """
        函数：根据整车参数self.vehicle_para和vx,计算矩阵A,B,C,并离散化状态空间方程
        return: None
        """

        vx = self.vehicle_vx
        (a, b, Cf, Cr, m, Iz) = self.vehicle_para

        # 1、A
        self.A[0][1] = 1

        self.A[1][1] = (Cf + Cr) / (m * vx)
        self.A[1][2] = -(Cf + Cr) / m
        self.A[1][3] = (a * Cf - b * Cr) / (m * vx)

        self.A[2][3] = 1

        self.A[3][1] = (a * Cf - b * Cr) / (Iz * vx)
        self.A[3][2] = -(a * Cf - b * Cr) / Iz
        self.A[3][3] = (a ** 2 * Cf + b ** 2 * Cr) / (Iz * vx)

        # 2、B
        self.B[1][0] = -Cf / m
        self.B[3][0] = -a * Cf / Iz

        # 3、C
        self.C[1][0] = (a * Cf - b * Cr)/(m * vx) - vx
        self.C[3][0] = (a ** 2 * Cf + b ** 2 * Cr)/(Iz * vx)

        # 4、A_bar、B_bar、C_bar
        dt = 0.1  # 状态空间方程离散化的时间间隔dt
        e = np.linalg.inv(np.eye(4) - (dt * self.A) / 2)  # np.linalg.inv()是矩阵求逆
        self.A_bar = e @ (np.eye(4) + (dt * self.A) / 2)
        self.B_bar = e @ self.B * dt
        self.C_bar = e @ self.C * self.k_r * self.vehicle_vx * dt

　　6、计算矩阵M、C、Cc、Q_bar、R_bar，再代入计算出二次规划的矩阵H_end、E_end，利用二次规划库求解出 $u_{k}$

    def cal_MPC_control_u(self, Q, R, F):
        """
        函数：由离散的状态空间方程的系数矩阵A_bar, B_bar, C_bar计算最优控制uk
        Q: 每一时刻误差代价的权重对应的对角矩阵，矩阵大小为self.m * self.m,对角线的数值越大算法的性能越好，但是会牺牲算法稳定性，而且最终控制量u很大。
        F: 终端时刻的误差代价的权重对应的对角矩阵，矩阵大小为self.m * self.m。
        R: 每一时刻控制代价的权重对应的对角矩阵，矩阵大小为self.p * self.p，对角线的数值越大越平稳，变化越小，控制效果越好，但是误差会很大。
        return: uk
        """

        # 1、计算M、C、Cc、Q_bar、R_bar
        M = np.zeros(shape=((self.n + 1) * self.m, self.m))
        M[0:self.m, :] = np.eye(self.m)
        for i in range(1, self.n + 1):
            M[i * self.m:(i+1) * self.m, :] = self.A_bar @ M[(i-1) * self.m:i * self.m, :]

        C = np.zeros(shape=((self.n + 1) * self.m, self.d * self.p))
        C[self.m:2 * self.m, 0:self.p] = self.B_bar
        for i in range(2, self.d + 1):
            C[i * self.m:(i + 1) * self.m, (i-1) * self.p:i * self.p] = self.B_bar
            for j in range(i-2, -1, -1):
                C[i * self.m:(i + 1) * self.m, j * self.p:(j + 1) * self.p] = self.A_bar @ C[i * self.m:(i + 1) * self.m, (j + ) * self.p:(j + 2) * self.p]

        Cc = np.zeros(shape=((self.n + 1) * self.m, 1))
        for i in range(1, self.n + 1):
            Cc[i * self.m:(i + 1) * self.m, 0:1] = self.A_bar @ Cc[(i - 1) * self.m:i * self.m, 0:1] + self.C_bar

        # 2、计算Q_bar、R_bar
        Q_bar = np.zeros(shape=((self.n + 1) * self.m, (self.n + 1) * self.m))
        for i in range(self.n):
            Q_bar[i * self.m:(i + 1) * self.m, i * self.m:(i + 1) * self.m] = Q
        Q_bar[self.n * self.m:(self.n + 1) * self.m, self.n * self.m:(self.n + 1) * self.m] = F

        R_bar = np.zeros(shape=(self.d*self.p, self.d*self.p))
        for i in range(self.d):
            R_bar[i * self.p:(i + 1) * self.p, i * self.p:(i + 1) * self.p] = np.eye(self.p) * R  # 确保R除了斜线有数据以外其他的为0

        # 3、计算代价函数的系数矩阵E_end和H_end  J = 0.5 * (x.T @ H_end @ x.T) + E_end.T @ x
        H_end = 2 * (C.T @ Q_bar @ C + R_bar)
        E_end = 2 * (C.T @ Q_bar @ Cc + C.T @ Q_bar @ M @ (np.array(self.err).reshape(self.m, 1)))
        P = H_end
        q = E_end
        print("P.shape", P.shape, np.linalg.matrix_rank(np.matrix(P)))   # np.matrix(P)将H转为矩阵形式，np.linalg.matrix_rank(np.matrix(P))是矩阵P的秩,判断P的秩

        # 4、约束项Gx < h
        lb = np.ones(shape=(self.d * self.p, 1)) * (-1)
        ub = np.ones(shape=(self.d * self.p, 1))
        G = np.concatenate((np.identity(self.d * self.p), (-1) * np.identity(self.d * self.p)))  # 矩阵G的大小(2dp, dp)，np.identity(2)是2×2的方阵
        h = np.concatenate((ub, (-1) * lb))  # 矩阵h的大小(2dp, 1)

        # 5、计算二次规划
        cvxopt.solvers.options['show_progress'] = False  # 为True的话展示过程
        res = cvxopt.solvers.qp(cvxopt.matrix(P), cvxopt.matrix(q), G=cvxopt.matrix(G), h=cvxopt.matrix(h))  # 将数组P、q、G、H转为矩阵代入cvxopt.solvers.qp二次规划求解库算出最终结果x

        return res['x'][0]  # 取控制量的第一个分量就是uk

　　7、设置Q、F、R，MPC控制输出转角 $u_{k}$

    def MPC_control(self):
        """
        函数：MPC控制算法
        return: steer_r
        """

        Q = np.eye(4)
        Q[0][0] = 250
        Q[1][1] = 1
        Q[2][2] = 50
        Q[3][3] = 1
        F = np.eye(4)
        b = 1
        R = b

        self.vehicle_info()
        self.cal_err_k_r(ts=0.1)
        self.cal_A_B_C_and_discretion()
        steer_r = self.cal_MPC_control_u(Q, R, F)

        return steer_r

Lateral_MPC_control = Lateral_MPC_controller(ego_vehicle, vehicle_para, pathway)
steer = Lateral_MPC_control.MPC_control()
print("steer:", steer)

最终完成了MPC的讲解，然后结合自动驾驶问题完成了MPC横向控制的代码。

汤姆_布利柏

关注

5
点赞
踩
32

收藏

觉得还不错? 一键收藏
3
评论
MPC---模型预测控制设计及基于CARLA的Python代码实现

理解MPC的概念与设计思路，构建MPC对应的二次规划的代价函数形式（系统状态变量的初始状态是已知的，只与控制有关）。然后求解使得代价函数J最小的控制，取向量的k时刻预测的u就是使得误差渐渐趋于0的最优控制。
复制链接

扫一扫