LMS算法的基本理论和MATLAB仿真
1 基本理论
最小均方算法,LMS算法,least-mean-square-algorithm





2 仿真
2.1 第一种信号:期望信号+噪声
2.1.1 没有蒙特卡洛
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS自适应滤波算法
% 由于射频前端低噪放、滤波等电路的不一致性,导致相同的接收信号通过接收通道后,
% 信号幅度和相位并不相同。为此,需要对通道的幅相误差进行校正。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fc=10e6; % 信号频率
fs=20*fc; % 采样频率
count=1024; % 采样点数
SNR=10; % 信噪比
t=0:1/fs:(count-1)/fs;
% LMS算法相关参数
M=50; % 滤波器的系数
Num_iteration=count; % 迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%----第一种信号
dn = sqrt(10^(SNR/10))*cos(2*pi*fc*t);% 期望信号
noise = randn(1,count); % 高斯白噪声
un = dn+noise; % 输入信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号处理
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
dn=real(dn); % 得到信号的实部
un=real(un);
un = un.';% 转置为列向量
dn = dn.';
% 求收敛常数
lamda_max = max(eig(un*un.'));%求解输入xn的自相关矩阵的最大特征值,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/lamda_max);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS算法
% 输入参数:
% un 输入信号 列向量
% dn 参考信号 列向量
% mu 步长因子 标量
% Num_iteration 迭代次数 标量
% M 滤波器阶数 标量
% 输出参数:
% w 滤波器的系数矩阵 M×Num_iteration 滤波器的系数是一个M列的列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
% en 误差信号 1×Num_iteration 每一次迭代后产生的误差
% yn 滤波器的输出信号 1×Num_iteration 行向量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 绘图
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
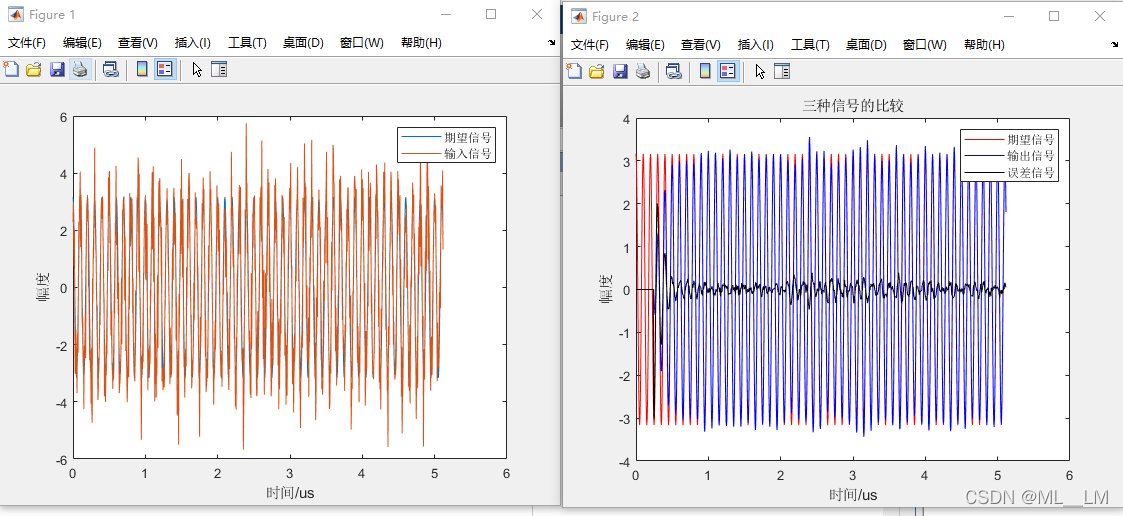
figure(1);
plot(t*1e6,dn);hold on;
plot(t*1e6,un);hold on;
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输入信号');
figure(2);
plot(t*1e6,dn,'-r');hold on;
plot(t*1e6,yn,'-b');hold on;
plot(t*1e6,en,'-k');
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输出信号','误差信号');
title('三种信号的比较');
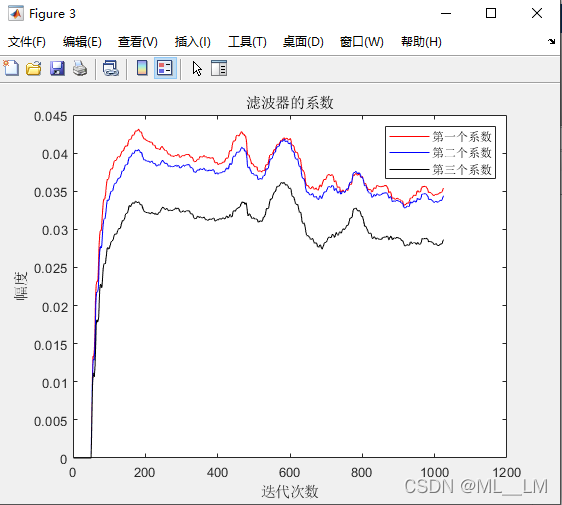
figure(3);
plot(w(1,:),'-r');hold on;
plot(w(2,:),'-b');hold on;
plot(w(3,:),'-k');hold on;
xlabel('迭代次数');ylabel('幅度');
legend('第一个系数','第二个系数','第三个系数');
title('滤波器的系数');
function [w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M)
%---------------LMS算法
% 滤波器的系数是一个列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
w = zeros(M,Num_iteration); % 滤波器系数的初始值
en = zeros(1,Num_iteration); % 误差信号的初始值
%---迭代更新滤波器的参数
for k = M:Num_iteration % 保证输入延时后的信号有效,所以实际的迭代次数只有(Num_iteration-M)次,
% 输入信号 向量U(n)=[u(n) u(n-1) ... u(n-M+1)]' 现代数字信号处理及应用的P134 式(4.1.4)
U = un(k:-1:k-M+1); % 将输入信号延迟,使得滤波器的每个抽头都有输入 式(4.1.4)
yn(k) = w(:,k)'*U; % 滤波器的输出信号 式(4.4.6) 共轭转置,不是转置
en(k) = dn(k)-yn(k); % 误差信号 式(4.4.7)
w(:,k+1) = w(:,k)+mu*U*conj(en(k));% 滤波器权向量的更新方程 式(4.4.8) conj 共轭
end
end
2.1.2 有蒙特卡洛
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS自适应滤波算法
% 由于射频前端低噪放、滤波等电路的不一致性,导致相同的接收信号通过接收通道后,
% 信号幅度和相位并不相同。为此,需要对通道的幅相误差进行校正。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fc=10e6; % 信号频率
fs=20*fc; % 采样频率
count=1024; % 采样点数
SNR=10; % 信噪比
t=0:1/fs:(count-1)/fs;
% LMS算法相关参数
M=50; % 滤波器的系数
Num_iteration=count; % 迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 蒙特卡罗仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Monte_Times=50; % 蒙特卡罗次数
sum_w=0;
sum_en=0;
sum_yn=0;
for p=1:Monte_Times
%----第一种信号
dn = sqrt(10^(SNR/10))*cos(2*pi*fc*t);% 期望信号
noise = randn(1,count); % 高斯白噪声
un = dn+noise; % 输入信号
dn=real(dn); % 得到信号的实部
un=real(un);
un = un.'; % 转置为列向量
dn = dn.';
% 求收敛常数
lamda_max = max(eig(un*un.'));%求解输入xn的自相关矩阵的最大特征值,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/lamda_max);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS算法
% 输入参数:
% un 输入信号 列向量
% dn 参考信号 列向量
% mu 步长因子 标量
% Num_iteration 迭代次数 标量
% M 滤波器阶数 标量
% 输出参数:
% w 滤波器的系数矩阵 M×Num_iteration 滤波器的系数是一个M列的列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
% en 误差信号 1×Num_iteration 每一次迭代后产生的误差
% yn 滤波器的输出信号 1×Num_iteration 行向量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M);
sum_w=sum_w+w;
sum_en=sum_en+en;
sum_yn=sum_yn+yn;
end
mean_w=sum_w/Monte_Times;
mean_en=sum_en/Monte_Times;
mean_yn=sum_yn/Monte_Times;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 绘图
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
plot(t*1e6,dn);hold on;
plot(t*1e6,un);hold on;
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输入信号');
figure(2);
plot(t*1e6,dn,'-r');hold on;
plot(t*1e6,mean_yn,'-b');hold on;
plot(t*1e6,mean_en,'-k');
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输出信号','误差信号');
title('三种信号的比较');
figure(3);
plot(mean_w(1,:),'-r');hold on;
plot(mean_w(2,:),'-b');hold on;
plot(mean_w(3,:),'-k');hold on;
xlabel('迭代次数');ylabel('幅度');
legend('第一个系数','第二个系数','第三个系数');
title('滤波器的系数');


2.2 第二种信号:期望信号+幅相误差
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS自适应滤波算法
% 由于射频前端低噪放、滤波等电路的不一致性,导致相同的接收信号通过接收通道后,
% 信号幅度和相位并不相同。为此,需要对通道的幅相误差进行校正。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fc=10e6; % 信号频率
fs=20*fc; % 采样频率
count=1024; % 采样点数
SNR=0; % 信噪比
t=0:1/fs:(count-1)/fs;
% 幅度和相位误差相关参数
thetas=30; % 目标入射角度
fines=50;
% LMS算法相关参数
M=50; % 滤波器的系数
Num_iteration=count; % 迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%----第二种信号
% 期望信号功率小于输入信号
dn = sqrt(10^(SNR/10))*exp(1j*2*pi*fc*t); % 期望信号
un=0.5*dn*exp(1j*pi*sind(thetas)*sind(fines)) ;% 输入信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号处理
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
dn=real(dn); % 得到信号的实部
un=real(un);
un = un.';% 转置为列向量
dn = dn.';
% 求收敛常数
lamda_max = max(eig(un*un.'));%求解输入xn的自相关矩阵的最大特征值,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/lamda_max);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS算法
% 输入参数:
% un 输入信号 列向量
% dn 参考信号 列向量
% mu 步长因子 标量
% Num_iteration 迭代次数 标量
% M 滤波器阶数 标量
% 输出参数:
% w 滤波器的系数矩阵 M×Num_iteration 滤波器的系数是一个M列的列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
% en 误差信号 1×Num_iteration 每一次迭代后产生的误差
% yn 滤波器的输出信号 1×Num_iteration 行向量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 绘图
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
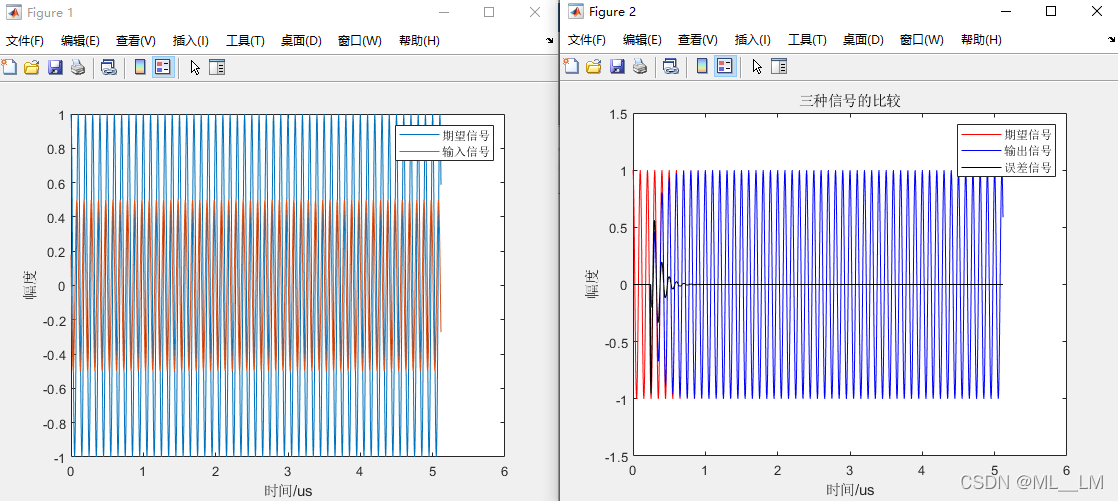
figure(1);
plot(t*1e6,dn);hold on;
plot(t*1e6,un);hold on;
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输入信号');
figure(2);
plot(t*1e6,dn,'-r');hold on;
plot(t*1e6,yn,'-b');hold on;
plot(t*1e6,en,'-k');
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输出信号','误差信号');
title('三种信号的比较');
figure(3);
plot(w(1,:),'-r');hold on;
plot(w(2,:),'-b');hold on;
plot(w(3,:),'-k');hold on;
xlabel('迭代次数');ylabel('幅度');
legend('第一个系数','第二个系数','第三个系数');
title('滤波器的系数');

2.3 第三种信号:期望信号+幅相误差+噪声
2.3.1 没有蒙特卡洛
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS自适应滤波算法
% 由于射频前端低噪放、滤波等电路的不一致性,导致相同的接收信号通过接收通道后,
% 信号幅度和相位并不相同。为此,需要对通道的幅相误差进行校正。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fc=10e6; % 信号频率
fs=20*fc; % 采样频率
count=1024; % 采样点数
SNR=10; % 信噪比
t=0:1/fs:(count-1)/fs;
% 幅度和相位误差
thetas=30; % 目标入射角度
fines=50;
% LMS算法相关参数
M=50; % 滤波器的系数
Num_iteration=count; % 迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%----第三种信号
% 期望信号功率小于输入信号
dn = sqrt(10^(SNR/10))*exp(1j*2*pi*fc*t); % 期望信号
noise = randn(1,count); % 高斯白噪声
un=2.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度大于期望信号,此时可以校正
% un=0.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度小于期望信号,此时不能校正
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 信号处理
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
dn=real(dn); % 得到信号的实部
un=real(un);
un = un.';% 转置为列向量
dn = dn.';
% 求收敛常数
lamda_max = max(eig(un*un.'));%求解输入xn的自相关矩阵的最大特征值,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/lamda_max);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS算法
% 输入参数:
% un 输入信号 列向量
% dn 参考信号 列向量
% mu 步长因子 标量
% Num_iteration 迭代次数 标量
% M 滤波器阶数 标量
% 输出参数:
% w 滤波器的系数矩阵 M×Num_iteration 滤波器的系数是一个M列的列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
% en 误差信号 1×Num_iteration 每一次迭代后产生的误差
% yn 滤波器的输出信号 1×Num_iteration 行向量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 绘图
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
plot(t*1e6,dn);hold on;
plot(t*1e6,un);hold on;
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输入信号');
figure(2);
plot(t*1e6,dn,'-r');hold on;
plot(t*1e6,yn,'-b');hold on;
plot(t*1e6,en,'-k');
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输出信号','误差信号');
title('三种信号的比较');
figure(3);
plot(w(1,:),'-r');hold on;
plot(w(2,:),'-b');hold on;
plot(w(3,:),'-k');hold on;
xlabel('迭代次数');ylabel('幅度');
legend('第一个系数','第二个系数','第三个系数');
title('滤波器的系数');


2.3.2 有蒙特卡洛
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS自适应滤波算法
% 由于射频前端低噪放、滤波等电路的不一致性,导致相同的接收信号通过接收通道后,
% 信号幅度和相位并不相同。为此,需要对通道的幅相误差进行校正。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
close all;
clear all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
fc=10e6; % 信号频率
fs=20*fc; % 采样频率
count=1024; % 采样点数
SNR=10; % 信噪比
t=0:1/fs:(count-1)/fs;
% 幅度和相位误差
thetas=30; % 目标入射角度
fines=50;
% LMS算法相关参数
M=50; % 滤波器的系数
Num_iteration=count; % 迭代次数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 蒙特卡罗仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Monte_Times=50; % 蒙特卡罗次数
sum_w=0;
sum_en=0;
sum_yn=0;
for p=1:Monte_Times
%----第三种信号
% 期望信号功率小于输入信号
dn = sqrt(10^(SNR/10))*exp(1j*2*pi*fc*t); % 期望信号
noise = randn(1,count); % 高斯白噪声
un=2.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度大于期望信号,此时可以校正
% un=0.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度小于期望信号,此时不能校正
dn=real(dn); % 得到信号的实部
un=real(un);
un = un.'; % 转置为列向量
dn = dn.';
% 求收敛常数
lamda_max = max(eig(un*un.'));%求解输入xn的自相关矩阵的最大特征值,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/lamda_max);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% LMS算法
% 输入参数:
% un 输入信号 列向量
% dn 参考信号 列向量
% mu 步长因子 标量
% Num_iteration 迭代次数 标量
% M 滤波器阶数 标量
% 输出参数:
% w 滤波器的系数矩阵 M×Num_iteration 滤波器的系数是一个M列的列矢量,Num_iteration表示迭代次数,每一次迭代都是一个列矢量
% en 误差信号 1×Num_iteration 每一次迭代后产生的误差
% yn 滤波器的输出信号 1×Num_iteration 行向量
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[w,en,yn] = my_LMS(un,dn,mu,Num_iteration,M);
sum_w=sum_w+w;
sum_en=sum_en+en;
sum_yn=sum_yn+yn;
end
mean_w=sum_w/Monte_Times;
mean_en=sum_en/Monte_Times;
mean_yn=sum_yn/Monte_Times;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 绘图
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure(1);
plot(t*1e6,dn);hold on;
plot(t*1e6,un);hold on;
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输入信号');
figure(2);
plot(t*1e6,dn,'-r');hold on;
plot(t*1e6,mean_yn,'-b');hold on;
plot(t*1e6,mean_en,'-k');
xlabel('时间/us');ylabel('幅度');
legend('期望信号','输出信号','误差信号');
title('三种信号的比较');
figure(3);
plot(mean_w(1,:),'-r');hold on;
plot(mean_w(2,:),'-b');hold on;
plot(mean_w(M-2,:),'-k');hold on;
plot(mean_w(M-1,:),'-g');hold on;
xlabel('迭代次数');ylabel('幅度');
legend('第一个系数','第二个系数','倒数第二个系数','倒数第一个系数');
title('滤波器的系数');


3 注意点
un=1.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度大于期望信号,此时可以校正
% un=0.5*dn*exp(1j*pi*sind(thetas)*sind(fines))+noise ;% 输入信号的幅度小于期望信号,此时不能校正
























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








