离散浣熊优化算法求解大规模多仓库多旅行商问题（Large - Scale Multi - Depot Multi - Traveling Salesman Problem， LS - MDMTSP）

一、问题定义

大规模多仓库多旅行商问题（Large - Scale Multi - Depot Multi - Traveling Salesman Problem，简称 LS - MDMTSP）是在经典旅行商问题基础上拓展而来的复杂组合优化问题。与单仓库情形不同，该问题设定了多个仓库，这些仓库均能作为旅行商的出发地与归宿。存在数量众多的客户节点分布在特定地理区域，同时有多支旅行商队伍。每支旅行商从各自选定的仓库出发，遍历若干客户节点后再返回出发仓库 。核心目标是确保所有客户节点都被至少一次访问，通常以最小化整体运营成本为优化方向，成本涵盖运输距离、时间消耗、车辆使用成本等多个维度。例如在全国性物流配送网络中，分布于不同城市的区域中心作为多仓库，各地的配送车辆作为旅行商，为分散在城市各处的客户提供服务。

二、问题特点

仓库选址与分配复杂性：不仅要考虑客户节点的分组和旅行商路径规划，还需合理确定每个旅行商从哪个仓库出发，以及如何将客户节点分配到各个仓库服务范围，这大大增加了问题复杂度。例如，不同仓库的运营成本、服务能力不同，需综合权衡。
规模庞大且复杂度高：随着客户节点、旅行商和仓库数量增加，解空间呈指数级膨胀。相较于单仓库问题，多仓库引入了更多变量，使得计算量和求解难度剧增。
多约束融合：除了单仓库多旅行商问题中的容量限制、时间窗约束、路径连通性约束外，还存在仓库容量约束，即每个仓库能够处理的货物量或服务客户数有限；以及仓库与旅行商的匹配约束，如特定旅行商只能从特定仓库出发等。

三、应用场景

区域物流协同配送：在城市群物流配送中，多个城市分别设有物流仓库，共同为区域内的企业和消费者提供货物配送服务。合理规划各仓库出发的配送车辆路径，能实现区域物流资源的高效利用，降低配送成本。
连锁企业物资调配：大型连锁超市或便利店，在不同地区设有多个配送中心（仓库），各配送中心派出配送车辆（旅行商）为旗下众多门店（客户节点）补货。优化调配方案可保障门店物资及时供应，同时减少配送资源浪费。
分布式能源巡检维护：在分布式能源系统中，存在多个能源管理中心（仓库），各中心派出巡检团队（旅行商）对分布在不同区域的能源设备（客户节点）进行定期巡检和维护。科学规划巡检路线，能提高能源系统的可靠性和稳定性。

四、常用求解方法

精确算法改进：针对大规模多仓库多旅行商问题，一些精确算法如分支定价法，通过将问题分解为定价子问题和主问题，利用列生成技术逐步生成最优解的列，相较于传统分支定界法，一定程度上提高了大规模问题的求解效率，但计算量依然较大，难以应对超大规模实例。
启发式与元启发式算法：
禁忌搜索算法：通过禁忌表记录已搜索过的解，避免算法重复搜索，引导搜索过程跳出局部最优解。在多仓库多旅行商问题中，用于探索不同的仓库 - 旅行商 - 客户节点组合，寻找较优路径。
模拟退火算法：模拟物理退火过程，从一个初始解出发，通过随机扰动产生新解，并以一定概率接受较差解，随着温度降低，逐渐收敛到全局最优解或近似最优解。在解决该问题时，可用于平衡全局搜索和局部搜索能力。
混合智能算法：将多种算法优势结合，如将遗传算法与局部搜索算法结合。先利用遗传算法的全局搜索能力对仓库分配和客户分组进行初步探索，再通过局部搜索算法对生成的路径进行精细优化，提高求解质量和效率。

五、案例分析

某大型快递企业在华东地区设有 5 个分拨中心（仓库），每天需向数千个快递网点（客户节点）派送包裹，涉及上百辆派送车辆（旅行商）。在未优化前，各分拨中心各自为政，派送路线混乱，导致成本高且派送时效低。通过引入基于混合智能算法的大规模多仓库多旅行商问题解决方案，对各分拨中心的服务范围重新划分，优化派送车辆路径。实施后，该地区快递派送成本降低了 20%，平均派送时效提高了 15%，有效提升了企业竞争力。

六、离散浣熊优化算法

离散浣熊优化算法（Discrete Coati Optimization Algorithm，DCOA）是一种受浣熊群体行为启发而开发的用于解决离散优化问题的智能优化算法。浣熊在自然界中具有复杂而有趣的行为模式，它们以群体为单位进行活动，在寻找食物、选择栖息地等过程中展现出了一种高效的协作和探索能力。DCOA 就是模拟浣熊群体在搜索食物和适应环境过程中的行为特征，将其抽象为数学模型和算法步骤，用于解决大规模多旅行商问题。

七、离散浣熊优化算法求解LS-MDMTSP

figure
hold on
new_pop = [];
for i = 1:m
    plot(city_coord(saleman_path{i},1),city_coord(saleman_path{i},2),'-o','MarkerSize',3,...
        'MarkerEdgeColor','b','LineWidth',2);
end
xlabel('X');
ylabel('Y');
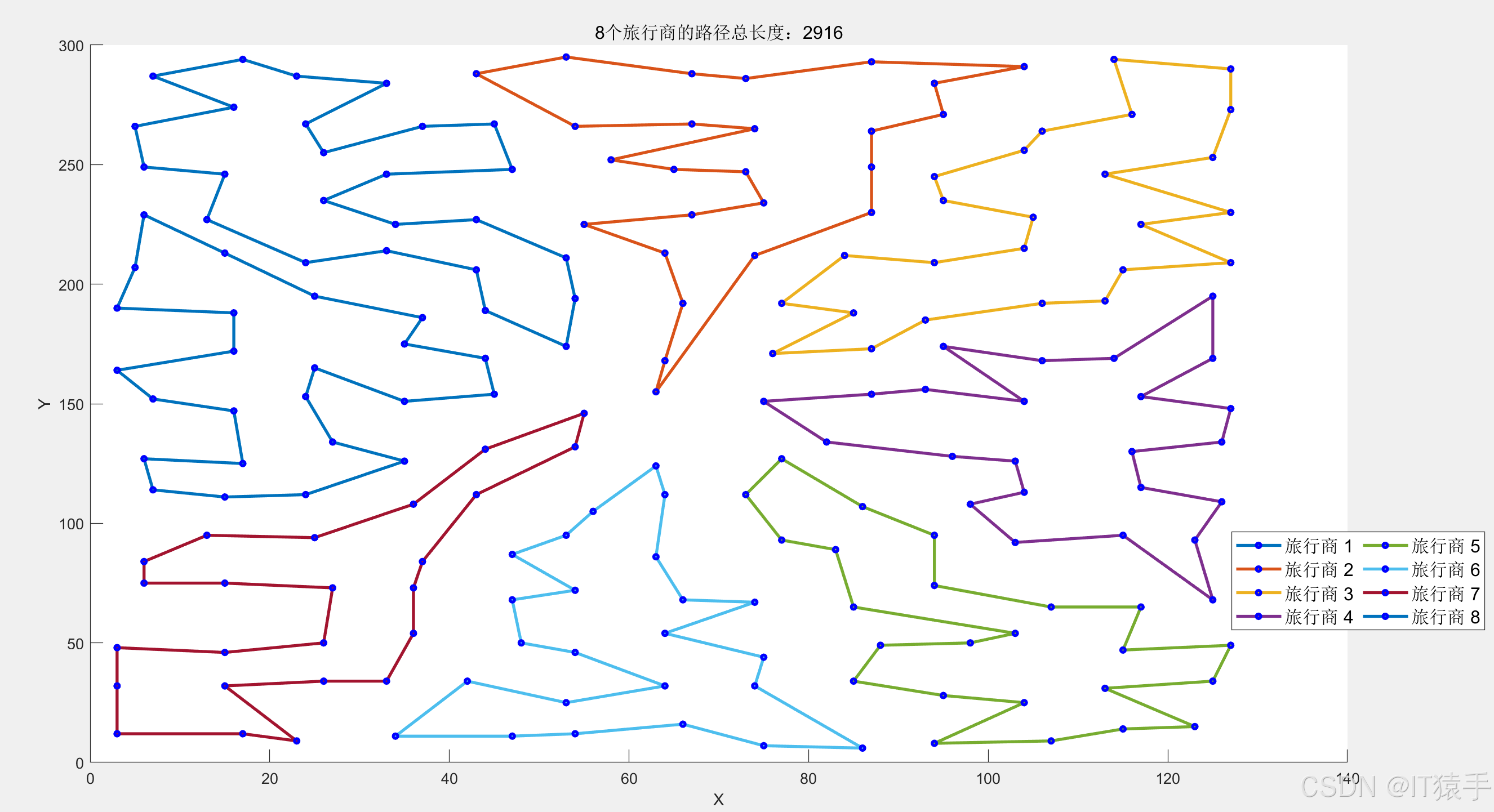
title([num2str(m),'个旅行商的路径总长度：',num2str(path_sum)],'FontSize',12);
lgd = legend(salemans,'FontSize',12,'TextColor','black');
lgd.NumColumns = 2;

figure
bar(path_length)
ylabel('路径长度')
set(gca,'xtick',1:1:m);
set(gca,'XTickLabel',salemans)

八、完整MATLAB见下方名片