电路中常用的定理及其应用分析

本文主要讲解电路分析中常用的定理，如叠加定理、戴维南定理、诺顿定理、最大功率传输定理和电源等效变换。

一、叠加定理

原理与适用范围

原理：在线性电路中，多个独立电源共同作用时，某支路的电流或电压等于各电源单独作用时在该支路产生的响应的代数和。

适用范围：仅适用于线性电路，不能用于计算功率（功率与电压/电流为平方关系）。

解题步骤

1.标出原电路待求量的参考方向。
2.依次保留一个电源作用，其他电源置零（电压源短路、电流源开路）。
3.分别计算各电源单独作用时的分量。
4.代数叠加各分量（注意方向是否一致）。

示例电路：

两个电压源US1=12V、US2=32V和电流源 IS=2A，电阻 R1=4Ω、R2=12Ω、R3=5Ω，求 R1的电流 I1 。

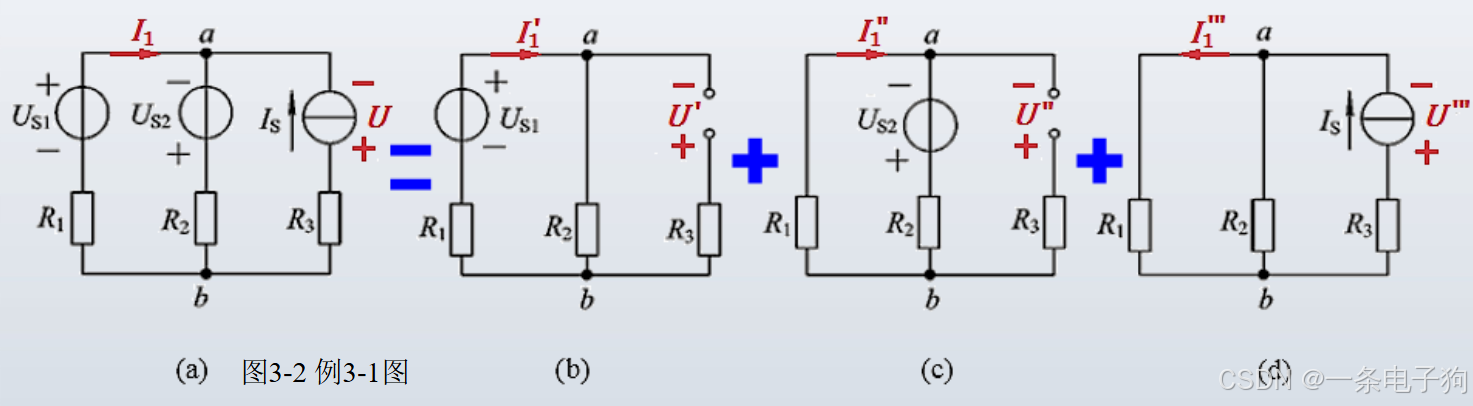
单独作用分析：
US1单独作用：

US2单独作用：

IS单独作用：

叠加结果：

二、戴维南定理

原理与适用范围

原理：任何线性有源二端网络可等效为电压源 Uoc与电阻 R0串联的电路，其中 Uoc是开路电压，R0是除源后等效电阻。

适用范围：适用于求复杂电路中某一支路的电流或电压。

解题步骤

1.断开待求支路，求开路电压 Uoc。
2.除源（电压源短路、电流源开路），求等效电阻 R0。构建等效电路，计算待求量。

示例电路：

Uoc=2V，RL=6Ω，求负载 RL的电流（原电路含多个电源和电阻）。

开路电压：断开 RL，计算端口电压 Uoc=2V。
等效电阻：除源后网络等效电阻 R0=4Ω。
等效电路为Uoc和R0串联的电路

三、诺顿定理

原理与适用范围

原理：线性有源二端网络可等效为电流源 Isc与电阻 R0并联的电路，其中 Isc是短路电流。

适用范围：与戴维南定理类似，但更适用于电流源等效场景。

解题步骤

1.求短路电流 Isc。
2.求等效电阻 R0（同戴维南定理）。
3.构建等效电路，计算待求量。

示例电路：

某二端网络测得 Uoc=10V、Isc=2A，则其诺顿等效电路为 Isc=2A与 R0=5Ω并联

四、最大功率传输定理

原理与公式

条件：当负载电阻 RL=R0（等效内阻）时，负载获得最大功率。

最大功率公式：

示例电路：

Uoc=20V、R0=5Ω，则 RL=5Ω时，

五、电源等效变换

原理与条件

电压源→电流源：IS=US/R ，并联电阻 R。
电流源→电压源：US=IS⋅R，串联电阻 R。
注意：仅对外电路等效，对内不等效

总结