DFT计算基本要素之一-倒易空间和k点

hhjc

已于 2023-03-31 08:09:52 修改

阅读量2.6k

点赞数 5

分类专栏： MS CASTEP的理论基础-密度泛函理论文章标签：分子模拟 DFT 布里渊区 k点选取

于 2023-03-30 21:30:07 首次发布

本文链接：https://blog.csdn.net/weixin_46465199/article/details/129737635

版权

MS CASTEP的理论基础-密度泛函理论专栏收录该内容

7 篇文章 8 订阅

订阅专栏

1平面波函数和布里渊区

2 k空间中的积分

Guass-Legendre（高斯-勒让德）求积方法 | Guass型求积公式 + Legendre多项式

3在布里渊区如何选择点

4 k空间的总结

收敛是执行DFT计算时候一个重要概念。就比如在本专栏第一篇文章，DFT所确定的原子构型基态电荷密度，就是由一组复杂的数学方程给出。为了在计算机上面实际求解这一问题，必须进行一系列数值近似：多维空间中的积分必须近似为该函数在有限点集合上面的积分；本应该表示为无穷多个加和项的解，也必须截断成有限个加和。对于这种数值近似，在计算次数逐渐增加时候，能得到更为精确的解，这一过程称之为收敛。

DFT计算数值收敛并不等价于求出了薛定谔方程的精确解，因为在做数学近似的时候截断丢失了本不应该丢掉的量，所以DFT计算存在计算精度问题，这个问题以后探讨。

1平面波函数和布里渊区

采用晶格矢量 $a_{1},a_{2},a_{3}$ 表示，在空间中重复的晶胞成为超晶胞。如果在这个周期性系统中求解薛定谔方程，特德解需要满足布洛赫定理的基本特点，该定理认为：所求的解可以表达成若干项的连加和，即：

$\phi \left ( r \right )=exp\left ( ik\cdot r \right )u_{k}\left ( r \right )$ （1）

式中： $u_{k}\left ( r \right )$ 在空间中具有与超晶胞相同的周期性，也就是对于任意整数 $n_{1},n_{2},n_{3}$ 有

$u_{k}\left ( r+n_{1}a_{1} +n_{2}a_{2}+n_{3}a_{3}\right )=u_{k}r$ （2）

该定理意味着可以用每一个k值分别独立的求解薛定谔方程。刚才是从薛定谔方程角度进行说明，该定理也同样适用于薛定谔方程这些解所衍生出来的其他物理量，例如电荷密度。

综合考虑来说，使用k求解DFT数学问题要比使用r更为方便。因为函数 $exp\left ( ik\cdot r \right )$ 称为波函数，所以采用这一计算思想的方法称之为波函数计算。矢量r的空间称之为实空间，矢量k的空间称之为k空间（倒易空间）。下面介绍k空间的一些特点。

在实空间中可以用晶格矢量 $a_{1},a_{2},a_{3}$ 的表达式来确定位置，同样的，在虚空间也可以定义三个矢量来确定位置，也就是所谓的倒格矢（ ReciprocalLatticeVectors ） $b_{1},b_{2},,b_{3}$ 并且如果 i=j 就有 $a_{i}\cdot b_{j}=2\pi$ ,否则就是0，这就有

$b_{1}=2\pi \frac{a_{2}\times a_{3}}{a_{1}\cdot \left ( a_{2}\times a_{3} \right )}$ $b_{2}=2\pi \frac{a_{1}\times a_{3}}{a_{2}\cdot \left ( a_{3} \times a_{1}\right )}$ $b_{3}=2\pi \frac{a_{1}\times a_{3}}{a_{3}\cdot \left ( a_{1} \times a_{2}\right )}$

对于实空间晶格矢量，一个很自然的选择就是对于所有i，都有 $\left | a_{i} \right |=a$ 。所以倒格矢满足 $\left | b_{i} \right |=\frac{2\pi }{a}$

对于该体系而言，晶格矢量和倒格矢都定义了立方体，前者边长是a,后者边长是 $\frac{2\pi }{a}$ .。

实空间的晶格矢量越大，则倒易空间中所对应的倒格矢越小。

倒格矢所定义的三维形状，并不是总是和实空间的超晶胞形状完全相同。对于FCC晶胞而言：

$a_{1}=a\left ( \frac{1}{2},\frac{1}{2},0 \right )$ $a_{2}=a\left ( 0,\frac{1}{2} ,\frac{1}{2}\right )$ $a_{3}=a\left ( \frac{1}{2} ,0,\frac{1}{2}\right )$

此时，倒格矢是

$b_{1}=\frac{2\pi }{a}\left ( 1,1,-1 \right )$ $b_{2}=\frac{2\pi }{a}\left ( -1,1,1 \right )$ $b_{3}=\frac{2\pi }{a}\left ( 1,-1,1 \right )$

下图画出了这些实空间的晶格矢量和倒格矢。

前面介绍过原胞的概念，就是完全定义一个无限扩展的周期性材料时，含有必要的最少的原子个数的超晶胞。也可以说原胞是含有所需信息的最小体积单元。

Wigner-Seitz定理：无论是对于实空间矢量，还是对倒易晶格矢量，都可以定义原胞。由于倒易空间的原胞具有很多特点，就专门对其进行命名，即布里渊区。布里渊区在材料能带理论中具有核心意义，对于布里渊区的几个特别重要的特点，进行单独的命名。最重要的就是K=0处，在k空间这个位置称之为 $\Gamma$ 点。为了完全说明实空间和倒易空间中长度的关系，将(布里渊区的缩写）体积记作为 $V_{BZ}$ ，根据Wigner-Seitz方法在实空间建立的原胞体积记作为 $V_{Cell}$ ,两者之间关系是：

$V_{BZ}=\frac{\left ( 2\pi \right )^{3}}{V_{cell}}$ （3）

2 k空间中的积分

为什么对于DFT计算来说，布里渊区那么重要？因为在实际的DFT计算中，所需要进行的大量工作可以归纳成求算下述形式的积分值，即：

$\overline{g}=\frac{V_{cell}}{\left ( 2\pi \right )^{3}}\int_{BZ}^{}g\left ( k \right )dk$ （4）

该积分主要特点就是：他是在倒易空间中定义的，并对布里渊区中所有可能的k值进行了积分。暂时不讨论这个值从哪来，先考虑如何求他的值。

在计算（4）式的积分值之前，先来看一个数值求算 $\int_{-1}^{1}f\left ( x \right )dx$ 的计算。这个意思就是可以看做在 $\left [ -1,1 \right ]$ 区间里面 $f\left ( x \right )$ 曲线下面所围成的面积。一开始学习的时候就知道，是将区间分为等区间长度的若干个区域，近似成梯形，然后估算每一段曲线底下的面积相加。可以利用梯形图解方法得到：

$\int_{-1}^{1}f\left ( x \right )dx\approx \frac{h}{2}\left [ f\left ( -1 \right ) +f\left ( +1 \right )+2 \sum_{j=1}^{n-1} f\left ( x_{j} \right )\right ]$ （5）

式中： $x_{j}=-1+jh$ , h=2/n

做一个求解一个简单例子来反应梯形求解精度问题。选取 $\int_{-1}^{1}\left ( \frac{\pi x}{2} sin\left ( \pi x \right )dx\right )$ ,这个函数积分值正好是1，比较直观反应问题

可以看出，选取的间距越小，所算值越精确。

梯形图解法具有两个特征，在 $f\left ( x \right )$ 估算位置之间，间距均匀相等；每一个 $f\left ( x \right )$ 估算值都使用了相同的权重（除了两侧端点）。还有一类更为精致的积分方法称之为高斯求积（ Gaussian Quadrature ）,形式为：

$\int_{-1}^{1}f\left ( x \right )dx\approx \sum_{j=1}^{n}c_{j}f\left ( x_{j} \right )$ （6）

式中：积分点 $x_{j}$ 对应于正交多项式的根，而权重 $c_{j}$ 与多项式积分有关。对于在 $\left [ -1,1 \right ]$ 区间上面的积分，这种方法称之为拉格朗日求积。下面给出一点具体例子，当n=3时候，式（6）权重和积分点分别为 $x_{1}=-x_{3}=\sqrt{\frac{3}{5}}$ , $x_{2}=0$ , $c_{1}=c_{3}=\frac{5}{9}$ , $c_{2}=\frac{8}{9}$ ,关于高斯-勒德让求积方法详解可以看

Guass-Legendre（高斯-勒让德）求积方法 | Guass型求积公式 + Legendre多项式

对上述的一位函数进行数值积分的例子可以总结为以下三点：

（1）通过将被积函数在一系列离散点上面进行估值，并在每一个点上面选择合适的权重，再对这些函数值加和，可以近似求算该积分。

（2）随着加和所使用的离散点个数增加，这种数值方法可以给出更精确的结果。假如所使用的点无限多，并对其取极限的时候，这些数值方法就收敛于积分的精确解

（3）在近似求解函数的积分的时候，对位置和权重的不同选择，会极大的影响该方法的收敛和获得更精确解的速度。

3在布里渊区如何选择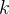点

对于类似式（4）的积分，因为所需要的DFT计算量大，所以对如何快速估算这些积分进行认真细致的研究，是十分有必要的。最为广泛使用的方法就是 Monkhorst 和 Pack 在1976年提出来的，绝大多数DFT计算软件都提供了基于该方法选定k点的选项。使用该方法，仅需要确定在倒易空间每个方向上面都使用多少个k点。对于每个晶格矢量长度都相等的超晶胞，他的倒格矢的长度也相等，因此在每个方向上使用相同数量的k点就很明显了。如果在每个方向上面都使用了M个k点，则将该运算标记为使用了 $M\times M\times M$ 个k点。

从以上有关数值积分的讨论中，可以明确的是如果 M> N ,那么使用 $M\times M\times M$ 个k点的计算应该能够给出更精确的结果。但是，实际上该怎样选择k点，以及选择多少个k点，应继续深究。

下图列出了使用 Monkhorst-Pack 方法所确定的 $M\times M\times M$ 个k点

可以看出，当M>8时候，可见总能几乎和k点个数无关，正如我们所期望的那样，k空间的计算数值收敛情况良好。然而，对于较少的k点，能量随着k点的个数变化任然很大，说明;较少的k点无法给出较好的收敛结果。

上表中最后一列是计算总能的时间除以M=1时计算时间的比值，达到确定收敛所需要的时间比只计算一个k点的时间要长很多。

一个比较令人费解的特征在于u，如果M是奇数，则对于M和M+1，二者的计算时间接近于相等。主要原因：这个计算利用了FCC晶体中所存在的大量对称性。这些对称性意味着：倒易空间的积分并不需要全部使用布里渊区来计算，而是可以使用一部分区域来估算这个积分。根据对称性，不需要进行任何近似，就可以使用这部分区域充满整个布里渊区。这个k空间中缩小的部分区域就是布里渊区（ Irreducible Brillouin Zone,IBZ ）。对于理想FCC晶体等对称性很高的材料，使用IBZ可以极大简化k空间中积分所需要的计算工作量。例如，在本例中如果采用 $10\times 10\times 10$ 的 Monkhorst-Pack 布里渊区取样，在k空间中只有35个独立的点位于IBZ内（如果计算时候没有任何对称性，则将会有1000个点）。

上表给出了每个计算在IBZ中k点的数量。将其与表中所列计算时间相比较，可以说明为什么奇数和偶数M计算时间基本相同-因为他们在IBZ中具有相同的独立k点个数。其发生的原因是：在 Monkhorst-Pack 方法中，使用奇数M包括了IBZ边界上面的一些k点，而偶数M只给出IBZ内部的k点。这意味着当使用少量k点时，使用偶数M比使用奇数M的收敛性好，二者的计算工作量基本相同。在能保证计算收敛，奇数和偶数M之间的区别就不那么重要。

为了表明对称性对减少DFT计算工作量的帮助，选用四原子超晶胞，并将每个原子从他原本的FCC晶格移动一个微小距离，然后重复上表计算。这些位移并不大，仅仅将最近邻原子改变 $\pm 0.09A$ ，但是改变了该体系的所有对称性，此时IBZ中的k点数量是 $\frac{M^{3}}{2}$ 。计算结果放在下表，也列出了 $\Delta E$ ，即有对称性和没有对称性之间的能量差。

尽管表中各个计算所用时间与IBZ中k点数量存在紧密联系，但是k空间中的计算收敛性仍然与全部布里渊区的k点密度相关。对于非对称体系而言，如果需要达到更高的能量收敛性，需要采用更大数量的k点来进行计算。

可以看出，随着k点的增大，能量差 $\Delta E$ 要比总能收敛快得多。这具有很多好处，因为相比于两种构型各自的绝对总能值，更值得注意的是两者之间的能量差，它具有更多的物理意义。因为对于某个原子构型的积分值，在任何一个k点集合上面所得到数值估算都与该系统的真实值存在一定系统误差。如果比较两种结构近似的原子构型，则可以做出以下预期：二者的这个系统性数值误差也非常近似。这意味着，当求算着两种状态之间的能量差值的时候，就抵消掉了他们的系统误差，计算得到的能量差要比相应的总能收敛更加精确。需要强调和理解的是，这个论断建立在如下基础上面：两种原子构型需要“足够近似”，才能让两者所使用的k点也非常近似。在上面所选取的例子中，两种晶体构型就非常近似，区别仅在于超晶胞中的原子位置存在很小的干扰，因此可以套用以上结论。当比较两种晶体结构完全不同的材料时，上述论断就不在合理。

很多时候，采用晶格矢量长度不同的超晶胞计算是非常有好处的。一个明显的例子就是采用具有以下晶格矢量的超晶胞，对体相Cu进行计算，即：

$a_{1}=a\left ( 1,0,0 \right )$ $a_{2}=a\left ( 0,1,0 \right )$ $a_{3}=a\left ( 0,0,4 \right )$

该超晶胞中含有16个原子，而在上述立方超晶胞中，只有四个原子。在对这个扩大的超晶胞进行计算时，只要在倒易空间中采用近似的k点密度，其计算的收敛精度也类似。根据该规则，采用 $8\times 8\times 2$ 个k点就可以得到合理的收敛精度，其中的三个数字分别指倒易晶格矢量 $b_{1},b_{2},b_{3}$ 方向上面k点的数量。根据倒易格矢的定义，可以得到：采用上述的k点设置方法，定义在倒易空间的每个方向上面都具有相同的k点密度。