绘制一张好看的散点图及pearson和spearman相关性分析的选择

上次谈到相关性分析，主要讲了pearson和spearman相关性分析：

（生物信息学）R语言与统计学入门（六）—— Pearson和Spearman相关性分析_Lijingxian教你学生信的博客-CSDN博客相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。相关性不等于因果性，也不是简单的个性化，相关性所涵盖的范围和领域几乎覆盖了我们所见到的方方面面，相关性在不同的学科里面的定义也有很大的差异。相关性分析主要包括pearson和spearman相关分析。比如比较两个基因之间的相关性，从而确定他们之间是否具有共表达关系。之前分享的关于GEPIA网站的两个基因相似性分析就是相关性分析：分享分https://blog.csdn.net/weixin_46500027/article/details/124030269?spm=1001.2014.3001.5501

 下面我们来用上次的数据，绘制一张好看的散点图：

数据格式准备如下，并将数据储存成csv格式：

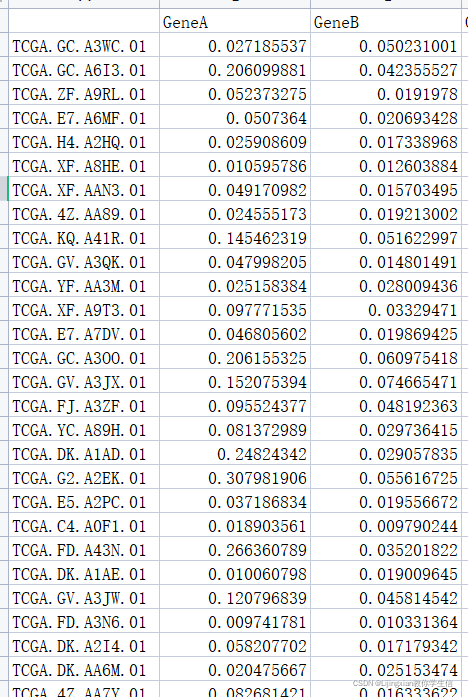
 下面开始绘制散点图：

读取文件：

setwd("D:\\")
dir()
data <- read.csv("PCC(1).csv",header = T,sep = ",")
head(data)

然后建一个线性模型：

model <- lm(data$GeneB~data$GeneA,data = data)
summary(model)

> summary(model)

Call:
lm(formula = data$GeneB ~ data$GeneA, data = data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.042368 -0.010605 -0.004979  0.003309  0.280395 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.023862   0.001442  16.548  < 2e-16 ***
data$GeneA  0.049984   0.006120   8.167 4.06e-15 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02273 on 405 degrees of freedom
Multiple R-squared:  0.1414,	Adjusted R-squared:  0.1393 
F-statistic:  66.7 on 1 and 405 DF,  p-value: 4.057e-15

下面就是画图：

library(ggplot2)
a <- ggplot(data = data,aes(x = data$GeneA,y = data$GeneB))+
  geom_point(shape = 19,colour = "dodgerblue3")+
  labs(y = "GeneA",x = "GeneB")
a

将线性模型传入图中：

b <- a+stat_smooth(method = lm,se = F,colour = "red")
b
g <- b+theme(plot.title = element_text(hjust = 0.5,size = 15),
             axis.title.y.left = element_text(size = 13,colour = "black"),
             axis.title.x.bottom = element_text(size = 13,colour = "black"))
g
h <- g+theme(axis.text.x.bottom = element_text(size = 12,colour = "black"))
h
i <- h +theme(axis.text.y.left = element_text(size = 12,colour = "black",
                                              vjust = 0.5,hjust = 0.5,
                                              angle = 90))

i

 最终得到下面图片：

 当然也可以去掉网格线和背景：

j <- i+theme_classic()
j

 

 颜色搭配可以参考之前的文章：

R语言中主要的颜色对照图_Lijingxian教你学生信的博客-CSDN博客R语言作图，颜色的选择是比较头疼的事情，以下向大家分享R语言中主要的几百种颜色。https://lijingxian19961016.blog.csdn.net/article/details/123245093?spm=1001.2014.3001.5502

那么如何选择pearson和spearman呢？

简单说，服从正态分布的连续性数据用pearson相关系数最恰当，当然也可以用spearman。

但是如果数据不符合正态分布，就用spearman相关系数，不能用pearson相关系数。

两个定序测量数据之间也用spearman相关系数，不能用pearson相关系数。

像我们上次的数据，我们首先来检查一下他们的正态性：

setwd("D:\\")
dir()
data <- read.csv("PCC.csv",header = T,sep = ",")
head(data)

shapiro.test(data$GeneA)
shapiro.test(data$GeneB)

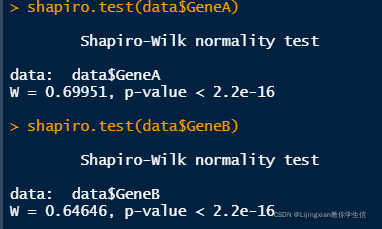
 可以看到，这两个数据都不符合正态分布，所以使用pearson相关分析是不太合适的，因此我们用spearman相关分析。

建议：既然spearman相关性分析任何条件下都适用，那么我们主要还是用spearman相关性分析比较好。

我们再看一看这两种方法计算的结果：

a <- cor.test(data$GeneA,data$GeneB,method = "spearman")
a

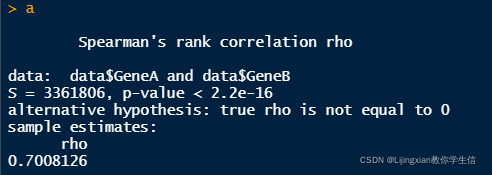
a <- cor.test(data$GeneA,data$GeneB,method = "pearson")
a

 可以看到，相差很大，所以不符合正态分布的还是不要用pearson相关分析。