电路理论实验报告5：串联谐振电路

​一、实验目的

⒈ 通过实验观察电路的串联谐振现象，加深对串联谐振电路特性的理解。

⒉ 通过实验学习测定电路的谐振频率f0,品质因数Q，并了解其意义。

3.掌握函数发生器的使用

二、实验原理

图3.10.1

 l．RLC串联电路（图3.10.1）的阻抗是电源角频率ω的函数，，当时，电路处于串联谐振状态，谐振角频率为：。显然，谐振频率仅与元件L、C的数值有关，而与电阻R和激励电源的角频率ω无关。当ω＜ω0时，电路呈容性，阻抗角φ＜0；当ω＞ω0时电路呈感性，阻抗角φ＞0。

 

2. 电路处于谐振状态的特性

（1）由于回路总电抗：，因此，回路阻抗 为最小值。整个回路相当于一个电阻，电源的电压与回路电流同相位。

（2）由于感抗ω0L和容抗1／ω0C相等，所以电感上的电压UL与电容上的电压UC大小相等，相位相差180º。谐振的感抗（或容抗）与电阻R之比称为品质因数Q。

在L和C为定值的条件下，Q值仅仅决定于回路电阻R的大小。

（3）在激励电压（有效值）不变的情况下，回路中的电流I=Us／R为最大值。

3．串联谐振电路的频率特性

（1）回路的响应电流与激励电源的角频率的关系称为电流的幅频特性（表明其关系的图形为串联谐振曲线），表达式为：

当电路的L和C保持不变时，改变R的大小，可以得出不同Q值时电流的幅频特性曲线（图3.10.2）；显然，Q值越高，曲线越尖锐。

为了反映一般情况，通常研究电流I／I0与角频率之比ω／ω0之间的函数关系：

这里，I0为谐振时的回路响应电流。

对于Q值相同的任何RLC串联电路只有一条曲线与之对应，所以，这种曲线称为串联谐振电路的通用曲线。

图10-2画出了不同Q值下的串联谐振电路的通用曲线。显然，Q值越高，在一定的频率偏移下，电流比下降得越厉害。

图3.10.2通用谐振曲线

串联谐振电路的通用曲线可以由计算得出，也可以用实验的方法测定。

为了衡量谐振电路对不同频率的选择能力，定义通用幅频特性曲线中幅值下降至峰峰值的0.707倍时的频率范围（见图3.10.2）为相对通频带（以B表示）即：

显然，Q值越高相对通频带越窄，电路的选择性越好。

（2）激励电压和回路响应电流的相角差φ与激励源角频率ω的关系称为相频特性，它可由公式：，计算得出或由实验测定。相角φ与ω／ω0的关系称为通用相频特性。

（3）串联谐振电路中，电感电压频率特性为：

电容电压的频率特性为:

UCmax=ULmax=

UC的峰值出现在ω＜ω0处，其中：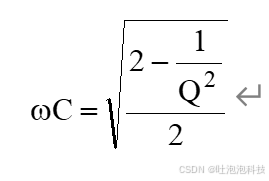    

UL的峰值出现在ω＞ω0处，其中：

Q值越大，出现峰值点离ω0越近。

三、实验内容

测量R=60Ω时电路的谐振频率f0

（1）本实验电路所用的电容、电感元件选自电容电感板，R使用多值电阻器，连接实验电路如图3.10.3所示。

例如，电路中取L=100mH、C=0. 1uF，R=60Ω

自行设计L,C,等参数，根据L,C配置相应的函数信号。

（2）调节函数信号发生器，使之输出正弦波，并使U1=3V（ UPP），接入电路；再调节函数信号发生器的输出信号频率，观测输出电压U2的变化，找到使U2达到最大值的频率，此频率就是使电路达到谐振的谐振频率，将此频率和测量的U2和UC的值，填入表3.10.1的中间部分，然后在谐振频率之下和谐振频率之上分别选4至5个测量点，将测量的频率值和电压值填入表3.10.1中。U1、U2均应用交流毫伏表测量出。

图3.10.3

频率（KHZ）	1192	1292	1392	1492	f0=1592	1692	1792	XXX	1992
U2（V）	0.452	0.640	1.02	2.13	3.88	1.59	0.940	0.672	0.527
UC（V）	9.94	12.96	XXX	37.40	63.83	24.60	13.74	9.30	6.93
UL（V）	5.72	8.76	15.04	33.73	XXX	28.53	17.88	13.49	11.14

四、实验报告

1）实验中怎样判断电路已经处于谐振状态？

答：电阻上的电压最大时电路谐振。

2、电感电压和电容电压相等时电路谐振。

3、线路中电流最大时电路谐振。

2）通过实验获得的谐振曲线分析电路参数对它的影响。

答：影响的是曲线的陡度,即品质因数Q,R越大,Q越低,波峰变缓.

3）怎样利用测得的数据求得电路的Q？

答：在谐振曲线峰值的0.707倍处做一直线与曲线相交，横坐标记做f1、f2，品质因数Q=f0/|f2-f1|