应用光学笔记04---平面镜棱镜系统

胖胖笔记

已于 2024-10-25 20:51:41 修改

阅读量3.2k

点赞数 17

分类专栏：应用光学文章标签：笔记 1024程序员节

于 2024-10-23 20:19:48 首次发布

本文链接：https://blog.csdn.net/weixin_47567773/article/details/143174035

版权

应用光学专栏收录该内容

8 篇文章

订阅专栏

共轴球面系统的物、光学系统和像位于一条直线上，不能拐弯，具有不便性。在共轴球面系统中加入平面镜棱镜系统，能够将共轴系统折叠以缩小仪器的体积减轻仪器重量；改变像的的方向，起倒像作用；改变共轴系统中光轴的位置和方向，形成潜望高或使光轴转一定角度；利用平面镜棱镜旋转，可以连续改变系统光轴方向，以扩大观察范围。

一、平面镜系统

1、平面镜的性质

1）单平面镜对单个物点成像：

对于任意物点A通过单个平面镜的成像情况，我们任取由A点射到平面镜P的光线AO和 $AO'$ ，根据反射定律作出射光线，出射光线反向延长线的交点即为像点 $A'$ 。图知 $\Delta ADO \sim \Delta A'DO$ ，由此可得 $AD=AD'$ 。

由此，单平面镜对单个物点成像：物像位置相对平面镜对称，物像大小相等；实物成虚像，虚物成实像；单个平面镜对物点能成理想像。

2）单平面镜对空间物体成像：

物像大小相等，形状不同（物空间右手坐标对应左手坐标，迎着 $z,z'$ 看 $xy,x'y'$ 时，当 $x$ 按逆时针方向转到 $y$ ， $x'$ 则按逆时针方向转到 $y'$ ；物像这种对应关系称为镜像）。

单平面镜成像性质：

对空间物体成像符合理想；

物像关于平面镜对称；

像的大小与物的大小相等；

成镜像，不相似

平面镜系统成像性质：成像理想；奇数个平面镜，成镜像；偶数个平面镜，物像相似。

2、平面镜的旋转

1）单个平面镜的转动

平面镜 $P$ 转动 $\alpha$ 变为 $P'$ ，法线 $N$ 随之转动 $\alpha$ 变为 $N'$ ，入射光线不变，入射角由 $I$ 变为 $I+\alpha$ 、出射光线由 $B$ 变为 $B'$ ，出射角为 $I+\alpha$ ，转动角 $\angle BOB'=2(I+\alpha)-2I=2\alpha$ 。入射光线不动，单个平面镜转动 $\alpha$ ，反射光线的转动量为 $2\alpha$ 。

由此，可应用于扩大观察范围

2）双平面镜的转动

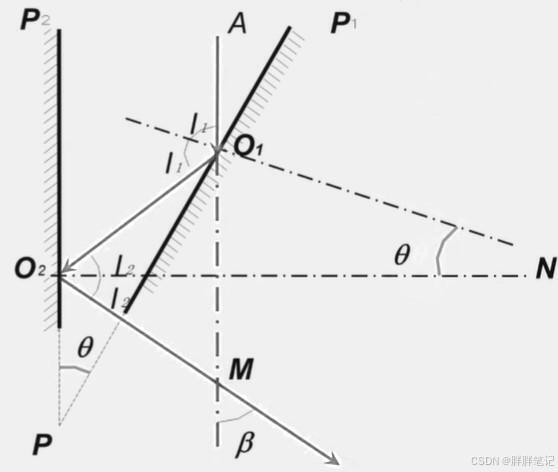
图中， $\beta$ 为出射光线与入射光线的夹角为， $\theta$ 为两平面镜法线的夹角。在 $\Delta O_1O_2M$ 中，外角 $2I_1=2I_2+\beta$ ；在 $\Delta O_1O_2N$ 中，外角 $I_1=I_2+\theta$ ；由此可得， $\beta=2\theta$ 。

光线的转角只与两个平面镜夹角有关，与入射光线的方向无关。不论入射光线的入射角和位置如何，出射光线与入射光线夹角不变，等于平面镜夹角的两倍。

由此，保证两个平面镜夹角不变，可以使入射光线和出射光线的夹角保持不变。将两个平面镜固定在刚性材料中可制成角镜。将反射面用玻璃实体包裹制成反射棱镜。

二、棱镜

反射棱镜：把一个或多个反射面作在同一块光学材料上，利用光线在介质内部的反射改变光线方向的光学零件。

棱镜相对于平面镜，优势在于光能损失少；坚固耐久，不易损坏；易于安装。劣势在于体积重量较大；材料要求高；受环境影响较大。

1、基本定义

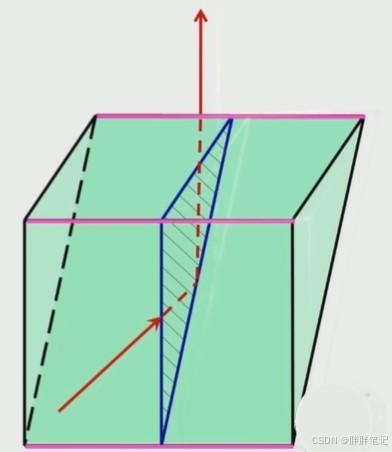
棱镜光轴：光学系统的光轴在棱镜中的部分。如下图：

工作面：棱镜的折射面和反射面统称为工作面。图中绿色平面。

棱：两工作面的交线。图中紫线

主截面：和各棱相垂直的截面。黑线所在平面

光轴截面：光轴所在的主截面。图中蓝线所围阴影面

2、棱镜的展开

下图为一个棱镜主截面光线示意图。光路为红色线，像为 $A'$ 。将反射面之后的光路和像点沿反射面对称翻折，如图中蓝色线所示。

由几何关系得 $\angle 1=\angle 2=\angle 3$

把棱镜的主截面沿反射面折倒，取消棱镜得反射，以平行玻璃板的折射代替棱镜折射的方法称为棱镜的展开。

棱镜和共轴球面系统组合后，仍能保持共轴球面系统的特性要求。棱镜的展开要求：

（1）棱镜展开后应该是一块两表面平行的玻璃板

（2）如果棱镜位于会聚光束中，光轴必须和棱镜的入射面及出射面垂直

3、典型棱镜的展开方法

1）直角棱镜

在平行光路中使用，只需要满足棱镜展开的第一个条件：平行玻璃板 $AB//A'C$ ，即 $\angle ABC=\angle A'CB=\angle ACB$ ，棱镜主截面为等腰三角形，称等腰棱镜。

在会聚光路中使用，除第一个条件外还需要满足第二个条件：入射出射表面与光轴垂直。

转90° ： $\angle A=90^{\circ} ,\angle ABC=\angle ACB=45^{\circ}$ ，展开长度 $L=D$ 。等腰直角棱镜。

转任意角度 $\alpha$ ：要求光线偏转 $\alpha$ ，则反射面偏转 $\alpha/2$ 。 $\angle B=\angle C=90^{\circ}-\frac{\alpha}{2}$

2）道威棱镜

对于直角棱镜在不同光轴转角时的通光口径，如下图所示。

当转角为90°时，通光口径 $D=a$ ；

当转角为0°时，若折射率为 $n$ ，入射角 $I=45^{\circ}$ ，由折射定律得 $sinI'=\frac{sin45{^{\circ}}}{n}=\frac{1}{n\sqrt{2}}$ ，因此 $cosI'=\sqrt{1-sin^2 I'}=\frac{1}{n\sqrt{2}} \sqrt{2n^2-1}$ ，通光口径 $D=EBsin45^{\circ}=\frac{AB-AE}{\sqrt{2}}=\frac{a-a \cdot tanI'}{\sqrt{2}}=0.7071a\frac{\sqrt{2n^2-1}-1}{\sqrt{2n^2-1}}$

若采用K9玻璃， $n=1.5163$ ， $D=0.334a$ 。

采用同样大小的直角棱镜，当光轴转角为0°时，通光口径仅有边长的1/3。因此实际应用中，切除直角棱镜上半段，留下的即为道威棱镜。

3）立方棱镜

为了增大通光口径，或者保证一定的通光口径下减小棱镜尺寸，可将两个直角棱镜沿着斜面粘接在一起，组成立方棱镜。

立方棱镜中，光束是分两束分别通过两个棱镜进入系统，过了棱镜又合成一束，原来角度一致的平行光通过系统后还应该角度一致，要求两个棱镜反射面严格平行。

入射圆形光束时，出设为两个半圆；不能在圆形光束中工作。

入射面与光轴不垂直，只能使用在平行光路中

4）五角棱镜

五角棱镜主截面展开过程如下图，如果光轴翻转90°，则两个反射面之间的夹角为45°。展开过程如下

如下图，根据几何计算可以得到 $L=(2+\sqrt{2})D$ 。

6）靴型棱镜

根据双平面镜的性质可知，光轴需要翻转90°，两个反射面之间夹角为45°。

光线经过第一个反射面时，入射角为60°，大于一般玻璃材料的临界角，发生全反射。经过第二个反射面时，入射角较小需要镀膜。

入射面和出射面之间的夹角为60°，人为加入补偿棱镜，以便于其展开。展开过程如下图

如下图，由几何关系计算可知 $L=\frac{4}{3}\sqrt{3}D$

注：补偿棱镜与靴型棱镜之间应留有间隙，确保在第一个反射面上能发生全反射；补偿棱镜的材料与靴型棱镜材料相同。

7）屋脊棱镜

观察棱镜对空间物体的成像发现，棱镜改变的是主截面内的成像方向。

实际问题中，通过棱镜系统后，成镜像，物像不相似。如下图

如果光轴方向 $x'$ 、主截面内像的方向 $y'$ 满足要求，如何改变 $z'$ 方向，使系统成相似像？

可用交线位于主截面内的两个相互垂直的反射面来取代原来的一个反射面，使垂直于主截面内的坐标被这两个相互垂直的反射面依次反射而改变方向，从而得到物体的相似像。

作用：在不改变光轴方向和主截面内成像方向的条件下，增加一次反射，使系统总反射次数由奇数变为偶数，达到物像相似的要求。

观察下图，x方向和y方向在屋脊棱镜主截面上，是在屋脊棱上发生反射，z方向垂直与主截面，经过两次反射后方向改变。

对屋脊面的要求：屋脊角必须严格等于90°，否则成双像。

对屋脊棱镜的展开方法与普通棱镜相同，沿着屋脊棱折倒。

在同样通光口径下，屋脊棱镜尺寸比一般棱镜要大。直角棱镜通过口径 $L=D$ 时，屋脊棱镜展开长度 $L=1.732D$ 。

屋脊棱镜的平面表示方式：在反射面上一条直线

4、棱镜的偏差

1）光学平行差

棱镜结构要满足展开的两个要求。因此如果棱镜存在几何形状误差，导致展开后两平面不平行，这种不平行性，称为“光学平性差”。

（1）第一光学平相差 $\theta_{\uppercase\expandafter{\romannumeral1}}$

棱镜展开后玻璃板在主截面内不平行度误差

（2）第二光学平性差 $\theta_\mathbb{I}$ ---棱差、尖塔差

棱镜展开后玻璃板在垂直于主截面方向上的不平行度误差。如图三棱柱变三棱锥

2）屋脊棱双像差

屋脊面之间夹角应等于90°。不等形成双像，双像差 $S=4n \delta$

三、平面镜棱镜系统的成像方向

1、平面镜棱镜系统的物像方向

用一个直角坐标系 $xyz$ 表示物空间。 $x$ ---与入射光轴重合； $y$ ---位于主截面内； $z$ ---垂直于主截面。

同样，用 $x'y'z'$ 表示像空间方向。

1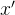） $x'$ 的方向

经平面镜与棱镜系统反射后，光轴出射方向即为 $x'$ 的方向。

2） $y',z'$ 的方向

（1）单一主截面的平面镜棱镜系统---系统中所有平面镜棱镜的光轴截面都重合

$z'$ ：没有屋脊面， $z,z'$ 方向相同；存在屋脊面， $z,z'$ 方向相反

$y'$ 的方向：

（a）没有屋脊面，光轴同向。偶次反射， $y,y'$ 同向；奇次反射， $y,y'$ 反向。

（b）没有屋脊面，光轴反向。偶次反射， $y,y'$ 反向；奇次反射， $y,y'$ 同向。

同向---光轴转角小于90°；反向---光轴转角大于9°；正好90°即可看作同向也可看作反向

另一种常用方法： $x'$ 的方向容易判断，已知 $y'$ 或者 $z'$ 的方向，根据总反射次数（镜像还是物像相似），确定另一个坐标的方向。

（c）存在屋脊面，由于屋脊面不影响主截面内成像方向，可以采用同样的法则判断 $y'$ 。但光轴在屋脊面上反射，计算光轴反射次数只算一次，系统总反射次数算两次。

（2）具有两个互相垂直的主截面的平面镜棱镜系统

系统中平面镜棱镜的光轴截面分两个方向，这两个方向互相垂直。棱镜仅改变主截面内物像方向，不改变垂直于主截面的成像方向。

如上图所示，棱镜1、3主截面平行，棱镜2主截面与之垂直。因此棱镜2只改变 $z'$ 的方向，棱镜1、3只改变 $y'$ 的方向。

棱镜2和棱镜1加3都属于单一主截面棱镜系统。分别使用之前的规则判断。

棱镜1使光轴顺时针转90°，棱镜3也使光轴顺时针转90°，二者共同转了180°。因此棱镜1加3光轴是反向的，又因为反射两次，所以 $y,y'$ 反向。

棱镜2使光轴转180°，光轴反向，反射两次，所以 $z,z'$ 反向。

2、平面镜棱镜系统的设计

设计一个由两个棱镜构成的平面镜棱镜系统，光轴有800mm潜望高，同时要求系统光轴位于同一平面内，物像相似并反向。

根据要求，采用两个使光轴改变90°的棱镜，构成具有单一主截面的棱镜系统。在以下三种棱镜中选择

要求出射和入射光轴同向，且物和像相反。所以要求主截面内光轴反射次数为奇数。只能采用一个90°-1的棱镜和一个90°-2的棱镜组合。

要求物像相似，之前设计系统反射次数为奇数，成镜像，所以将某一个反射面改为屋脊棱镜。形成以下四个系统

四、共轴球面系统与平面镜棱镜系统的组合

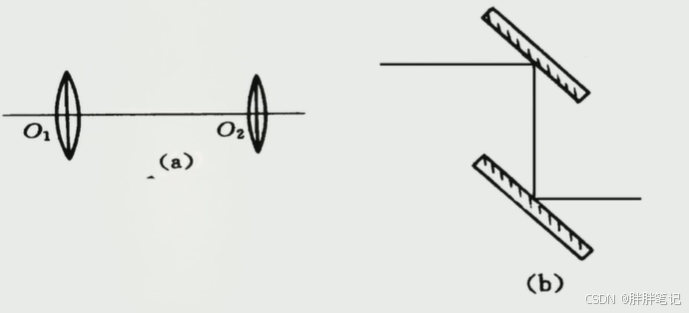
1、共轴球面系统与平面镜系统的组合方法

各个透镜组和平面镜的配合次序不受限制
为了保持共轴系统的对称性，各透镜组的光轴需和平面镜系统中同一共轭轴线相重合
为了保持共轴系统光学特性不变，需使各透镜组之间的间隔不变

2、共轴球面系统与棱镜系统的组合方法

配合次序不是任意的。如果共轴球面系统的光轴与棱镜的入射表面不垂直（例如立方棱镜），则该棱镜只能放在平行光束中，否则将破坏系统的共轴性。
必须考虑平行玻璃板产生的像面位移

平行玻璃板成像不符合理想，设计时需要与共轴球面系统一起综合考虑

3、共轴球面系统与平面镜棱镜系统组合时，成像方向的判断

先分别确定共轴球面系统、平面镜棱镜系统的成像方向
共轴球面系统成倒像，系统成像方向与平面镜棱镜系统的成像方向相反；共轴球面系统成正像，系统成像方向与平面镜棱镜系统的成像方向相同。

对于棱镜系统为单一主截面系统，光轴同向，反射次数为3次， $y,y'$ 反向；存在屋脊面， $z,z'$ 反向。

将棱镜系统和开普勒望远系统（目镜物镜均为正透镜，成倒像）相配合，将平面镜棱镜系统的成像方向再翻转。