人眼与目视光学系统配合时,相当于整个系统中的一个子光学系统。如下图为望远系统+人眼

一、人眼
1、人眼的光学结构
从光学角度看,人眼可以看作由镜头、底片和光阑三大部分组成,这三个部分恰好是一台照相机的组成。对于人眼的分析可以类比为一台照相机,能够自动调节。角膜、前室和晶状体相当于照相机镜头,视网膜和黄斑相当于感光底片,虹膜中心瞳孔直径可放大或缩小,相当于可变光阑。

2、人眼的光学特性
人眼近似看为一个共轴球面系统
1)基本定义
视轴(光轴):眼睛黄斑中心与眼睛光学系统的像方节点连线
视场:人眼观察范围。可达150°。头不动,能看清视轴中心6°-8°

2)人眼的功能:视度调节和瞳孔调节
(1)视度调节
随着物体距离改变,人眼自动晶状体前表面的半径。从而改变焦距,使像落在视网膜上。

视度SD:上述过程中,人眼自动调节的量。视网膜相共轭的物面到眼睛距离的倒数(单位
1/米)
明视距离:正常人眼在正常照明状态下的正常阅读距离。通常为眼睛前方250mm,
近点:眼睛通过调节,肌肉收缩到最紧张距离时,能看清物体的最短距离。
远点:眼睛完全放松时,能够看清物体的最远距离。
最大调节范围=近点视度-远点视度

(2)瞳孔调节
虹膜可以自动改变瞳孔大小,以控制人眼的进光量。强光/白天,;夜晚
。设计光学仪器时,仪器的出射瞳孔要和人眼瞳孔大小配合。

3)分辨率
两物点在视网膜上成俩个个像点,若两个像点距离较大,人眼能够分辨开两个像点;若两个像点距离小到一定程度,人眼可能分辨不出使两个像点。

人眼视网膜由是神经细胞组成,包含有分锥状细胞和杆状细胞。如果两像点落在两个不相邻的视神经细胞上,它们之间的距离大于两视神经细胞,能够分清楚是两个像点。视神经细胞直径约为,选取0.006mm在物空间所对应的张角,称为视角分辨率。

视角分辨率:刚刚能被人眼分辨开的两物点之间的最小视角。
由无限远处物体理想像高公式得
对线的分辨率(读10秒)
二、目视光学仪器
目视光学仪器是一类直接用于人眼观察的设备,例如望远镜、显微镜和瞄准镜等。因此它需要满足一些要求。
1、对目视光学仪器的共同要求
1)增大视角
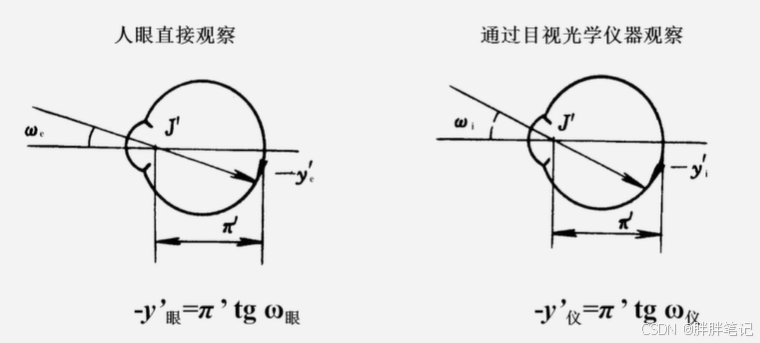
用仪器观察物体时视网膜上的像高',与用人眼直接观察物体时视网膜上的像高
之比,表示仪器的放大能力。用
表示。
视放大率:,通过仪器观察的视角正切与人眼直接观察时视角正切之比。
2)目视光学仪器所成的像位于无限远
正常人眼在自然状态下,无限远物体成像在视网膜上,为避免人眼观察时眼睛疲劳,目视光学仪器所成的像也应该位于无限远。
2、放大镜和显微镜的工作原理
下图为人眼观察眼睛前方距离处高度为
的物体的示意图

根据几何关系可知,物体对人眼的张角
要求最小视角
提高视角的途径:
减小物距?物距需要大于近点,它的调节存在限制
提高物高?跟我们分辨细微物点的出发点违背,但可以借助目视光学仪器将物高放大,再进一步通过人眼观察。
1)放大镜
放大镜:对近距离/小物体进行放大,供人眼观察的仪器

位于放大镜物方焦点的物体经过放大镜后成一束平行光,此时,用人眼直接观察
,为了让人眼观察,一般
(明视距离)。由此视放大率为
。
如果,则要求
,要提高放大镜的视放大率,就需要减小透镜焦距,但对于一个简单的单正透镜,由焦距公式
可知,焦距越小,球面半径越小,加工难度越大,因此焦距不可能很小。
因此可以增大放大镜物方焦平面上的物高,由此设计了显微镜。
2)显微镜
工作原理:运用一组透镜先将物体放大成像在放大镜的物方焦点上,再通过放大镜放大供人眼观察。放大镜的“物”高增加了,人眼看到就是二次放大的像

物镜(objective):对着物体的透镜
目镜(eyepiece):对着人眼的透镜
光学筒长:从物镜像方焦平面到目镜物方焦平面的距离
用人眼直接观察,
用显微镜观察的,运用牛顿公式
可知
,所以
,视放大率
显微镜的视放大率等于物镜的垂直放大率乘以目镜的视放大率
考虑理想光学系统组合像方焦距公式
有,
,形式上跟放大镜一样,所以显微镜可以看为一个复杂的放大镜。
3、望远镜的工作原理
首先,运用一组透镜将无限远的物体成像在其像方焦平面处;随后,运用单个放大镜将其物方焦平面处的像成像在无穷远。第一组透镜的像方焦平面和放大镜的物方焦平面重合。

对着物方的透镜为物镜(objective),对着人眼的透镜为目镜(eyepiece)。光学筒长
物镜的像方焦点和目镜的物方焦点重合
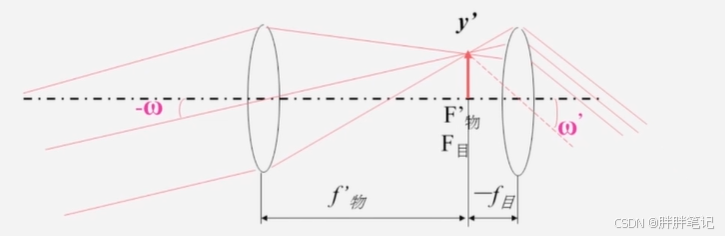
视放大率,由图知
,
,望远系统的视放大率
要增大视角,及要求
,物镜的焦距大于目镜的焦距
的正负号由物镜和目镜焦距的正负号决定,
,
同号,成正像;
,
异号,成倒像。
物镜和目镜的焦距均为正---开普勒望远镜
,成倒像。系统中存在实像,可安装分划板,进行测量和瞄准,常用于制作军用光学仪器

物镜焦距为正,目镜焦距为负---伽利略望远镜
,成正像。系统中不存在实像,不能安装分划板,无法进行测量和瞄准,常用于观察。

对于轴上点发出的光线,望远系统的仪器视角就为物点发出光线的孔径角,人眼的视角就为系统出射光线的孔径角
由角放大率定义,视放大率
望远镜的角放大率不随共轭面的位置变化而变化,数值上等于视放大率

根据垂轴放大率与角放大率的关系式, 望远镜的垂直放大率也不随共轭面的位置变化而变化,数值上等于视放大率的倒数
入射光束大小,出射光束大小
,望远镜
4、目视光学仪器的调节
1)眼睛的缺陷和校正
正常人眼在自然状态下,无限远物体成像在视网膜上,即像方焦点与视网重合。

正常人眼观察近距离物体时,依靠人眼视度调节可以将点前移,使像成在视网膜上。人眼能看清的最远距离称为远点,远点是人眼自然状态下与网膜像相共轭的物平面位置;人眼依靠调节能看清的最近距离称为近点。
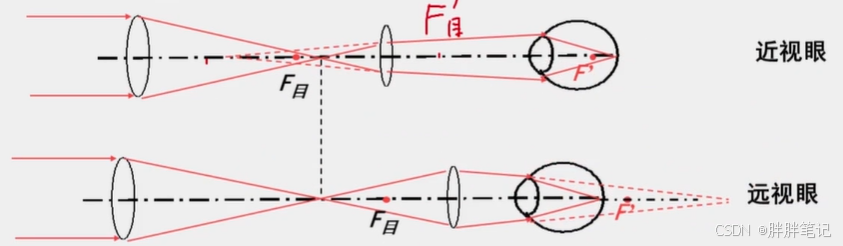
其一,人眼中存在近视眼,像方焦点在视网膜前方,无限远物不能成像在视网膜上。近视眼看不清无限远目标,看到的最远距离(远点)有限。

近视程度:远点距离所对应的视度表示。医学上眼睛的度数与视度相对应,1视度=100°。
近视眼校正---采用焦点等于远点距离的负透镜

其二,人眼存在远视眼,像方焦点在视网膜后方,依靠调节有可能看清无限远物体。

远视眼的远点在眼睛后方,近点距离比正常人眼增加。
远视眼校正---采用焦距等于远点距离的正透镜

2)目视光学仪器的视度调节

以望远系统为例,正常眼观察时,物镜的像方焦点和目镜的物方焦点重合;近视眼观察时,需要将目镜靠近物镜移动,使得物镜的像方焦点位于目镜的物方焦点的右方;远视眼观察时,需要将目镜远离物镜移动,使得物镜的像方焦点位于目镜的物方焦点的左方。
调节量的计算:我们一般通过调节目镜的方式对系统进行调节。因此根据牛顿公式可以计算。
其中,就是目镜的调节量;
为目镜的像距,即远点到像方焦点
![]() 的距离,
的距离,
因此利用牛顿公式可得
实际应用中,目镜的镜圈上刻有相应的视度值,转动目镜,实际就是调节视度。
5、双眼观察仪器
1)空间深度感觉和双眼立体视觉
单眼判断远近:物高已知,根据视角判断;根据物体之间遮蔽关系和日光阴影;物体细节程度和空气透明度;眼睛调节紧张程度。
闭上一只眼睛,试着给笔套上笔帽,即使小心翼翼地确认距离,但是还是很难办到。
立体视觉---体视
体视产生的原因是视差角不同的造成的。
若A、B离眼睛距离相同,此时,
都在
同侧;
。人眼观察A、B两点位于同一深度。

若A、B离眼睛距离不同,第一种情况,位于
两侧;第二种情况,
位于
同侧,但
。可以看到
,人眼产生了立体视觉。

视差角之差的大小标志着物体远近差别的大小。
时,人眼就分不清A、B的远近区别,这一极限值
称为体视锐度。
体视半径:人眼有体视的最大距离。

设A在无穷远,人眼刚好能区分B点不在无穷远处,
体视误差:在体视范围内,对两物体是否处在同一空间深度判断的误差。,该式子仅适用于

视差角等于双眼瞳距比观察距离,对其两边同时取微分,并用差商代替微商则
,把
代入得
。
2)双眼观察仪器
 (1)体视放大率
(1)体视放大率
若人眼直接观察的视差角为,通过仪器后视差角放大为
,则体视放大率定义为

人眼直接观察时,
进入仪器物方视差角,仪器像方的视差角
因此,人眼基线b=62mm,则
(2)体视误差
由得
,对其两边取微分得
从仪器像方进入人眼得最小视差角为10'',因此双眼观察仪器的体视误差为,人眼直接观察体视误差
,
。因此采用双眼观察仪器后体视误差减小。
(3)双眼仪器的要求
| 左右光轴平行 |
|
| 左右两系统放大率一致 | |
| 左右两系统不应该有像倾斜 |

























 6385
6385

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








