Chapter5:连续性和可导性(两种类型的光滑性)
5.连续性和可导性
连续性:直觉上告诉我们,连续函数的图像必须能一笔画成
可导性:直觉上告诉我们,在可导函数的图像中不会出现尖角
5.1 连续性 (笔不离纸画曲线)
在一点处连续、在区间上连续
5.1.1 在一点处连续


例子1:
下图中左极限
≠
\neq
=右极限,所以双侧极限不存在

例子2:
下图函数在
x
=
a
x=a
x=a 处无定义,
f
(
a
)
f(a)
f(a)不存在

例子3:
下图双侧极限与
f
(
a
)
f(a)
f(a)不等

例子4:
下图函数在
x
=
a
x=a
x=a 处连续

5.1.2 在一个区间上连续(函数在区间内每个点都连续)
[
a
,
b
]
[a,b]
[a,b]

(
a
,
b
)
(a,b)
(a,b)

单侧连续性:函数定义域包括一个带有左端点和 / 或右端点的区间
右连续
x
∈
[
a
,
b
)
lim
x
→
a
+
f
(
x
)
=
f
(
a
)
x\in [a,b)\\ \lim_{x \rightarrow a^+}f(x)=f(a)
x∈[a,b)x→a+limf(x)=f(a)

左连续
x
∈
(
a
,
b
]
lim
x
→
b
−
f
(
x
)
=
f
(
b
)
x \in (a,b] \\ \lim_{x \rightarrow b^-}f(x)=f(b)
x∈(a,b]x→b−limf(x)=f(b)


5.1.3 连续函数的一些例子
1.一个连续函数的常数倍是连续的
2.两个连续函数做加法、减法、乘法、复合,会得到另一个连续函数
3.一个连续函数除以另一个连续函数(除分母为0外)商函数处处连续
4.所有的指数函数和对数函数都是连续的
5.所有的三角函数也是连续的(除了在它们渐近线上)

5.1.4 介值定理





介值定理的应用:方程的解
例子:证明方程
x
=
c
o
s
(
x
)
x=cos(x)
x=cos(x) 有一个解
不需要求出解的具体值,只需证明存在一个解即可
小窍门:将所有表达式放到等号左边
f ( x ) = x − c o s ( x ) = 0 f(x)=x-cos(x)=0 f(x)=x−cos(x)=0 证明 f ( c ) = 0 f(c)=0 f(c)=0
y = x y=x y=x是连续函数, y = c o s ( x ) y=cos(x) y=cos(x)是连续函数,故 f ( x ) f(x) f(x)是连续函数
选取
a
=
0
,
b
=
π
2
a=0,b=\frac{\pi}{2}
a=0,b=2π
f
(
x
)
f(x)
f(x)在区间
(
a
,
b
)
(a,b)
(a,b)上连续
f
(
a
)
=
0
−
c
o
s
(
0
)
=
−
1
<
0
f(a)=0-cos(0)=-1 \lt 0
f(a)=0−cos(0)=−1<0
f
(
b
)
=
π
2
−
c
o
s
(
π
2
)
=
π
2
>
0
f(b)=\frac{\pi}{2}-cos(\frac{\pi}{2})=\frac{\pi}{2} \gt 0
f(b)=2π−cos(2π)=2π>0
由介值定理得,在区间
(
0
,
π
2
)
(0,\frac{\pi}{2})
(0,2π)上存在常数
c
c
c 使得
f
(
c
)
=
0
f(c)=0
f(c)=0,于是证明了方程
x
=
c
o
s
(
x
)
x=cos(x)
x=cos(x) 至少有一个解
5.1.5 较难的介值定理例子
证明:任意的奇数次多项式至少有一个根(对于偶数次多项式不成立)
p
(
x
)
=
a
n
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
0
x
0
p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_0x^0
p(x)=anxn+an−1xn−1+⋯+a0x0



5.1.6 连续函数的最大值和最小值

为了确保可以使用最大值与最小值定理,连续性区间必须是闭的
闭区间
[
a
,
b
]
[a,b]
[a,b]内函数连续,函数至少有一个最大值和一个最小值

闭区间
[
a
,
b
]
[a,b]
[a,b]内函数不连续,函数无最大最小值
开区间
(
a
,
b
)
(a,b)
(a,b)端点无定义,函数可能有最大最小值,也可能没有,也可能只有最大值或者只有最小值

5.2 可导性(函数图像无尖角)
5.2.1 平均速率

5.2.2 位移和速度



5.2.3 瞬时速度
开始时间
t
t
t,终止时间
u
u
u




不能用 u = t u=t u=t 作替换,会得到 0 0 \frac{0}{0} 00
令
h
=
u
−
t
h=u-t
h=u−t,当
u
u
u 越来越靠近
t
t
t 时,
h
→
0
h\rightarrow 0
h→0

5.2.4 速度的图像阐释

斜率就是时间段
(
t
,
u
)
(t,u)
(t,u) 的平均速度


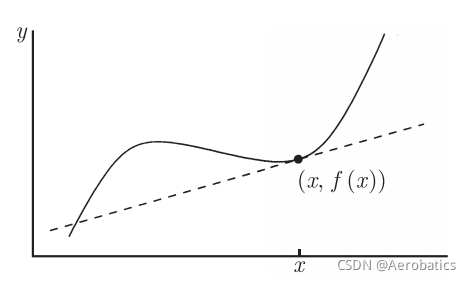
5.2.5 切线
切线不是只能与曲线仅相交一次
下图函数图像在
x
=
0
x=0
x=0 处出现尖角,故函数在此点处无导数

5.2.6 导函数


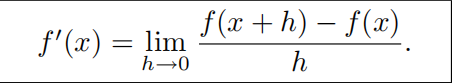
函数不可导的原因之一

5.2.7 作为极限比的导数
量
h
h
h 代表对
x
x
x 作了多少改变,因此用
Δ
x
\Delta x
Δx 作替换




极限的重要阐释

上图公式的重要阐释

函数求导的目的:当对函数
f
f
f 求关于变量
x
x
x 的导数时,只是为了看一下当对
x
x
x 做极小变动时函数
f
(
x
)
f(x)
f(x) 有什么变化
例子:
f
(
x
)
=
x
2
,
f
′
(
x
)
=
2
x
f(x)=x^2,f'(x)=2x
f(x)=x2,f′(x)=2x
当
x
=
6
x=6
x=6 时,
f
(
6
)
=
36
,
f
′
(
x
)
=
12
f(6)=36,f'(x)=12
f(6)=36,f′(x)=12
当
x
x
x 变化
0.01
0.01
0.01 时,则函数值
36
36
36 将会变化
12
×
0.01
12×0.01
12×0.01,因此猜测
f
(
6.01
)
=
36.12
f(6.01)=36.12
f(6.01)=36.12
而实际结果为
36.1201
36.1201
36.1201,出现误差
上述误差的原因:
f ′ ( x ) f'(x) f′(x) 并不真正地等于 Δ y \Delta y Δy 和 Δ x \Delta x Δx 的比值,它等于当 Δ x \Delta x Δx 趋于 0 0 0 时该比值的极限
dy/dx的理解



dy/dx根本不是一个分数

5.2.8 线性函数的导数
f
(
x
)
=
m
x
+
b
f(x)=mx+b
f(x)=mx+b
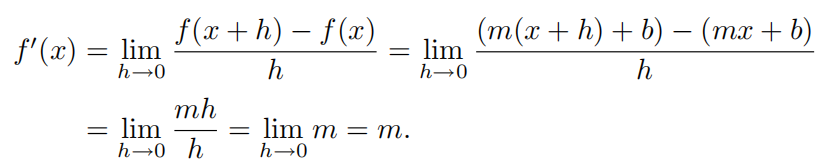
5.2.9 二阶导数和高阶导数
f
′
(
x
)
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
d
y
d
x
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\frac{dy}{dx}
f′(x)=Δx→0limΔxΔy=dxdy
f
′
′
(
x
)
=
lim
Δ
x
→
0
f
′
(
x
+
Δ
x
)
−
f
′
(
x
)
Δ
x
=
d
d
x
(
d
y
d
x
)
=
d
2
y
d
x
2
f''(x)=\lim_{\Delta x\rightarrow 0}\frac{f'(x+\Delta x)-f'(x)}{\Delta x}=\frac{d}{dx}(\frac{dy}{dx})=\frac{d^2y}{dx^2}
f′′(x)=Δx→0limΔxf′(x+Δx)−f′(x)=dxd(dxdy)=dx2d2y
零阶导
f
(
0
)
(
x
)
f^{(0)}(x)
f(0)(x)(原函数,未进行求导)
三阶导
f
(
3
)
(
x
)
f^{(3)}(x)
f(3)(x)
四阶导
f
(
4
)
(
x
)
f^{(4)}(x)
f(4)(x)
n
n
n 阶导
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)
5.2.10 何时导数不存在
右导数

左导数

如果 左导数与右导数 存在且相等,那么实际导数存在且有相同的值

x
>
0
,
f
′
(
x
)
=
1
x \gt 0,f'(x)=1
x>0,f′(x)=1
x
<
0
,
f
′
(
x
)
=
−
1
x \lt 0,f'(x)=-1
x<0,f′(x)=−1
左侧斜率
≠
\neq
= 右侧斜率,在
x
=
0
x=0
x=0处导数不存在
5.2.11 可导性和连续性

可导

连续

证明可导必连续


























 824
824

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










