Chapter17:微积分基本定理
17.微积分基本定理
17.1 用其他函数的积分来表示函数

当变量
x
x
x 在
t
t
t 轴上变化时,面积
F
(
x
)
F(x)
F(x) 的大小也在相应变化
函数
F
F
F主要是由被积函数
f
(
t
)
f(t)
f(t)和常数
a
a
a决定的。
改变
a
a
a的值仅仅使函数值增加或减少一个常数(即一块面积)

17.2 微积分第一基本定理

17.2.1 微积分第一基本定理的大致证明











17.2.2 积分下限不影响积分求导的结果

可以这样理解: v − t v-t v−t图像的面积为汽车位移,水平轴为时间,积分下限为起始时间 a a a,位移对时间的导数代表汽车的速度,上面提到常数a的选择(也就是初始时间)不会影响这个求导结果(也就是汽车速度),这样显然是合理的
17.3 微积分第二基本定理

17.3.1 微积分第二基本定理的大致证明

∫
a
b
f
(
x
)
d
x
=
F
(
x
)
∣
a
b
=
F
(
b
)
−
F
(
a
)
\int_a^bf(x)dx=F(x)\bigg|_a^b=F(b)-F(a)
∫abf(x)dx=F(x)∣
∣ab=F(b)−F(a)
17.4 不定积分
计算定积分的方法:
- 黎曼和的极限
- 反导数
反导数(即导数的原函数)
如果两个函数具有相同的导数,那这两个函数的差是个常数
所有反导数之间的差都是一个常数

下面三个函数是
F
(
x
)
F(x)
F(x) 的反导数,它们之间相差一个常数
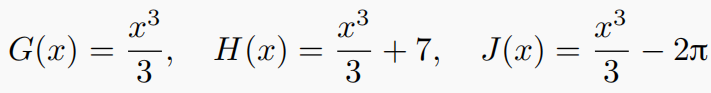
现寻找一种简单表示反导数的方式
不定积分表示:“函数
f
f
f的反导数的集合”
(函数 f 的各个反导数因常数不同,所以所有的反导数组成了集合)


17.4.1 定积分和不定积分的不同

17.4.2 不定积分的两个性质


17.5 使用微积分第一基本定理解决问题
用实际变量替代虚拟变量
例子:

17.5.1 变量是积分下限
方法:前面添加负号,再互换积分上下限使用第一基本定理
例子:

17.5.2 积分上限是一个函数
不能直接使用第一基本定理
方法:将积分上限换元,然后使用链式求导法则,最后用第一基本定理
例子:

17.5.3 积分上下限都是函数
方法:用一个常数把积分分成两部分,然后都变为积分上限是函数,利用换元法、链式求导法则,第一基本定理
这个常数只要在被积函数的定义域内即可
例子:

17.5.4 导数伪装成极限

17.6 使用微积分第二基本定理解决问题
17.6.1 计算不定积分
只要知道一个函数的导函数,就一定会知道此导函数的反导数
导数和积分公式


微分公式中,如果使用
a
x
ax
ax 替代
x
x
x 那每一个相应的公式乘以
a
a
a

积分公式中,如果如果使用 a x ax ax 替代 x x x,那每一个相应的公式除以 a a a

17.6.2 计算定积分
使用微积分第二基本定理求解定积分方法:
- 先求对应的不定积分
- 分别把积分上下限代入不定积分,变为定积分
- 求差


























 1677
1677

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










