§3.4 函数的单调性
![]() 在
在![]() 上小于零,在
上小于零,在![]() 上大于零。
上大于零。
函数的单调性是否与导函数的符号有关呢?为此,我们进一步地作图,希望从中获得更多的感性认识。
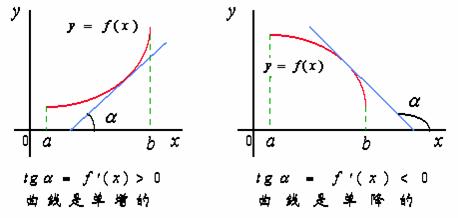
函数![]() 在
在![]() 上单调增加(减少),则它的图形是一条沿
上单调增加(减少),则它的图形是一条沿![]() 轴正向上升(下降)的曲线, 曲线上各点处的切线之斜率均为正的(负的),即:
轴正向上升(下降)的曲线, 曲线上各点处的切线之斜率均为正的(负的),即:
![]() (
(![]() )
)
这表明:函数的单调性确实与其导数的符号有关,因此,可以利用导数的符号来判定函数的单调性。
二、函数单调性的判别法
设函数![]() 在
在![]() 上连续, 在
上连续, 在![]() 上可导,
上可导,![]() ,则
,则
![]()
若在![]() 内
内![]() ,则
,则![]() ,从而
,从而 ![]() ;
;
即: 函数![]() 在
在![]() 上单调增加;
上单调增加;
若在![]() 内
内![]() ,则
,则![]() ,从而
,从而 ![]() ,
,
即: 函数![]() 在
在![]() 上单调减少。
上单调减少。
综上讨论, 我们有如下结论:
【函数单调性判别法】
设函数![]() 在
在![]() 上连续, 在
上连续, 在![]() 上可导,
上可导,
(1)、若在![]() 内
内![]() , 则
, 则![]() 在
在![]() 上单调增加;
上单调增加;
(2)、若在![]() 内
内![]() , 则
, 则![]() 在
在![]() 上单调减少。
上单调减少。
注明:
1、判别法中的闭区间若换成其它各种区间(包括无穷区间),结论仍成立。
2、以后把函数单调的区间称之为函数的单调区间。
【例1】讨论函数![]() 的单调性。
的单调性。
解:函数的定义域为![]() , 且
, 且
![]()
当![]() 时,
时, ![]() , 故函数在
, 故函数在![]() 上单调减少;
上单调减少;
当![]() 时,
时, ![]() , 故函数在
, 故函数在![]() 上单调增加。
上单调增加。

【例2】讨论函数![]() 的单调性。
的单调性。
解: 函数的定义域为![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() , 故函数在
, 故函数在![]() 上单减;
上单减;
当![]() 时,
时, ![]() ,
, ![]() , 故函数在
, 故函数在![]() 上单增。
上单增。


因此,可以通过求函数的一阶导数其符号不确定的点,将函数的定义域分划成若干个部分区间,再判定函数一阶导数在这些部分区间上的符号,继而可决定函数在这些部分区间上的单调性。
【例3】试确定函数 ![]() 的单调区间。
的单调区间。
解: 当![]() 时,函数无定义, 故函数在
时,函数无定义, 故函数在![]() 处不可导;
处不可导;
当![]() 时, 导函数为
时, 导函数为 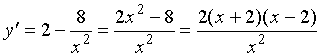
令![]() 得:
得: ![]()
于是, 点![]() 将函数定义域(
将函数定义域( ![]() )分划成四个区间
)分划成四个区间 ![]() 、
、![]() 、
、![]() 、
、![]() ,函数在这四个区间上的单调性如下:
,函数在这四个区间上的单调性如下:
在![]() 上,
上, ![]() , 函数
, 函数![]() 单增;
单增;
在![]() 上,
上, ![]() , 函数
, 函数![]() 单减;
单减;
在![]() 上,
上, ![]() , 函数
, 函数![]() 单减;
单减;
在![]() 上,
上, ![]() , 函数
, 函数![]() 单增。
单增。
【例4】讨论函数![]() 的单调性。
的单调性。

【结论】
一般地,如果![]() 在某区间上的有限个点处为零, 而在其余各点处均为正(或负)时,那么
在某区间上的有限个点处为零, 而在其余各点处均为正(或负)时,那么![]() 在该区间上仍是单调增加(或单调减少)的。
在该区间上仍是单调增加(或单调减少)的。
利用函数的单调性可以证明较为复杂的函数不等式。
【例5】试证明:当![]() 时, 有
时, 有 ![]()
解:作辅助函数 ![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
故 ![]() ,
,
![]() 在
在![]() 上单调增加,从而有
上单调增加,从而有 ![]() ,
,
而 ![]() ,
,
于是 ![]() ,
,![]() 在
在![]() 上也单调增加。
上也单调增加。
从而有 ![]() ,
,
即 ![]() 。
。
该证明方法十分典型,对于一些较精细的函数不等式的证明可借助些法。
























 5280
5280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








