SDF函数之三角形原理详解（Shadertoy绘制三角形）

SDF函数之三角形原理详解（Shadertoy绘制三角形）

参考IQ大佬的代码（三角形）代码网址：
https://iquilezles.org/articles/distfunctions2d/
参考博客博客网址：
https://blog.csdn.net/qq_41368247/article/details/106194092
首先个人觉得SDF函数绘制三角形比较有代表性，相比于圆、矩形、与正方形的SDF比较难以理解，而且作者也是被三角形的SDF函数绘制折磨了好几天，还好有人给我推荐了这篇博客，才恍然大悟。😬😬😬
个人觉得该篇博客写的非常好，但其原理解释的并不是很详细，尤其是映射部分，一笔带过，所以想要补充完善一下，而且也算是对自己这段时间学习的知识进行一个总结整理。
首先展示一下源码与生成三角形情况。

一、代码与SDF生成三角形展示

1、Shadertoy代码

// SDF三角函数
float sdEquilateralTriangle(  in vec2 p, in float r )
{
    const float k = sqrt(3.0);
    p.x = abs(p.x) - r;
    p.y = p.y + r/k;
    if( p.x+k*p.y>0.0 ) p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0;
    p.x -= clamp( p.x, -2.0*r, 0.0 );
    return -length(p)*sign(p.y);
}

// 主文件
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
	// 归一化处理
	vec2 p = 3.*(2.0*fragCoord.xy-iResolution.xy)/iResolution.y;  
	vec3 col = vec3(0.7,0.2,0.9); // 颜色
	float d = sdEquilateralTriangle( p, 1.0 ); // 三角形绘制   
	col = mix( col, vec3(0.), smoothstep(0.0,0.02,d) ); //平滑处理
	fragColor = vec4(col,1.0);		// 输出
}

2、生成的三角形

这里为了后续好区分，选用紫色。

二、SDF三角形函数原理讲解

1、前言

个人理解，SDF函数就是想办法将形状内部全部转换为负数，而形状外部的全部转换为正数，在边线上正好为零，这样才是有向距离函数。

2、简单代码分析

为了更好的理解，我们使用该博客的代码写在这个上面，把三角形的SDF函数单独拿出来，代码一句一句的看。

float sdEquilateralTriangle(in vec2 p, in float r )
{
    const float k = sqrt(3.0);
    p.x = abs(p.x);
    if( p.x+k*p.y>0.0 ) p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0;
    p.x -= r;
    p.y += r/k;
    p.x -= clamp( p.x, -2.0*r, 0.0 );
    return -length(p)*sign(p.y);
}

针对于代码1：const float k = sqrt(3.0);
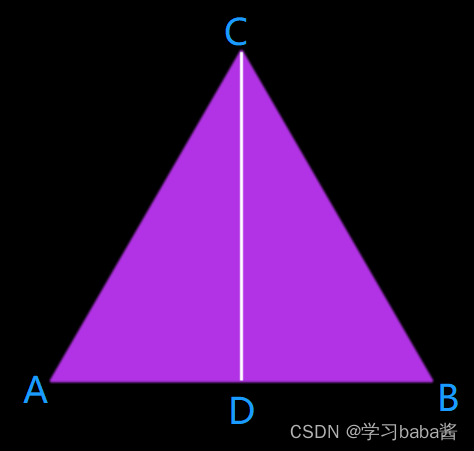
这句代码主要是为了确定一个常量，为后续计算做准备，为什么选择为 $\sqrt{3}$ 作为常量呢，因为假设等边三角形的边长为$2r$，那么对应高的垂线即为 $\sqrt{3}r$，如下图所示，BD为$r$，BC为$2r$$，\angle BCD=30°$，则根据勾股定理求得CD为 $\sqrt{3}r$。

针对于代码2：p.x = abs(p.x);
这句代码比较常用，即基本上关于$y$轴对称的图形都会进行这样一次映射，不用考虑$x$的负半轴事情了。

3、重点代码分析

针对于代码3：if( p.x+k*p.y>0.0 ) p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0;这句代码是重中之重。
我们可以首先参考这篇博客，得知三角形可以看成由三个部分绕中心点三个角度生成的，如下图所示。而且在第二行代码，已经将$x$的负半轴进行了一次映射，即在$x$正半轴做的事情，负半轴也会做一遍。所以我们只需考虑区域1的部分（注意：区域1是包括AOB三角形的整片区域与空白区域）。
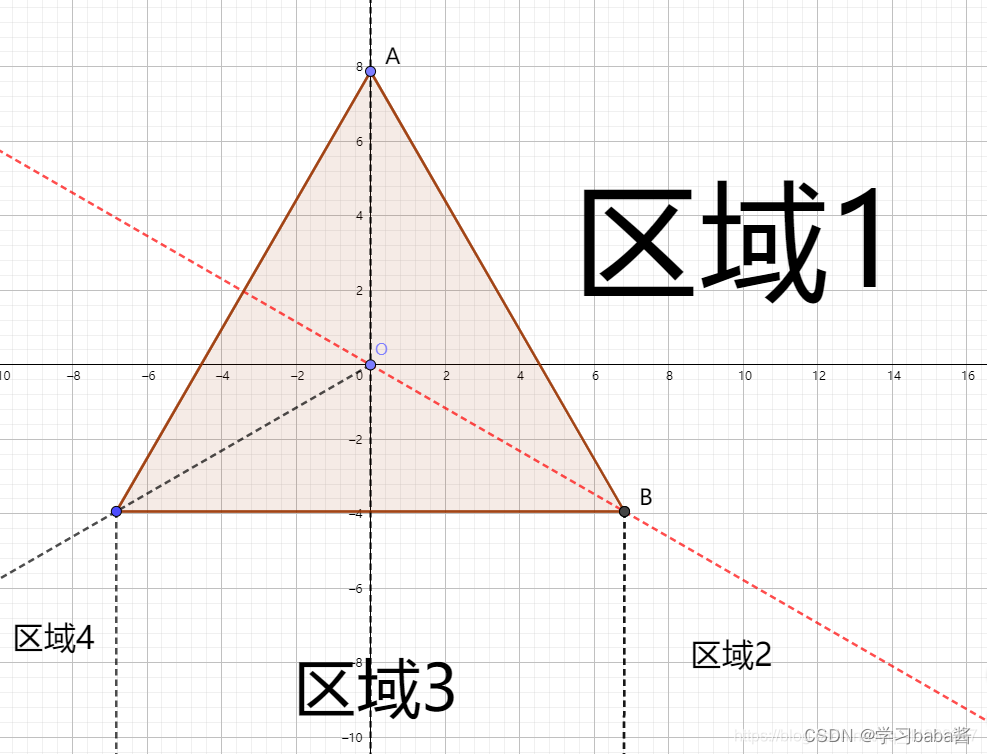（借用一下该作者的图，ps：T-Jhon）
为什么要考虑映射，因为只有映射到下半区域，即区域3，后续我们才比较容易进行计算与判断。
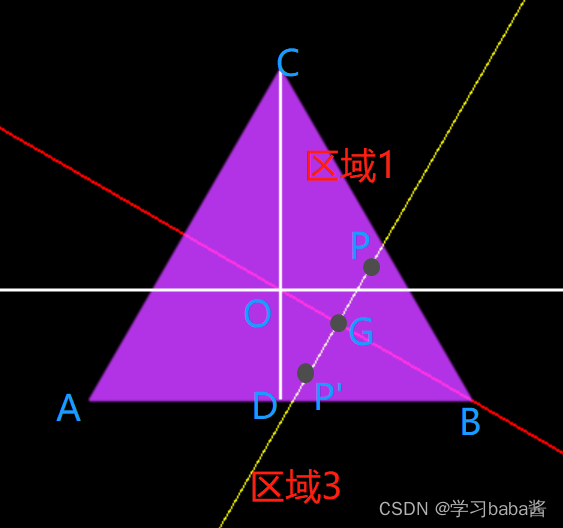
那么我们需要根据那条线段进行映射呢？我们可以观察下图。
（白色线段分别代表$x$轴与$y$轴，红色线段BE正好将三角形对称分割）

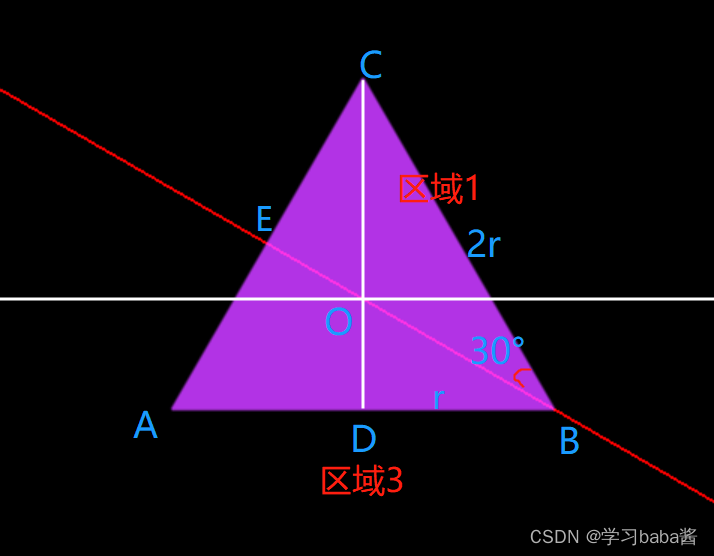
这里可以观察到红色线段BE是可以将区域1的部分映射到区域3的部分，那么红色线段的关系式是多少呢？

注：任何映射都可以想象为将纸折叠一次，本文这里将这张纸沿着线段BE进行折叠，▲BEC全部折叠到了▲BEA上面，但是我们要记住，刚刚的$x$负半轴我们是不考虑的，所以是将▲BOC沿着BE折叠到了▲BOA。

我们已知$BD=r$，$\angle OBD=30°$，由勾股定理得$OD=\frac{\sqrt{3}}{3}$，又因为D点在$y$的负半轴上，所以点B为$(r，-\frac{\sqrt{3}}{3}r)$。
又因为线段BE过原点O，所以线段BE的关系式为：
$$y_1=-\frac{\sqrt{3}}{3}{x}_1$$
我们的目的是什么？
将区域1上的所有的点都映射到区域3上面，注意，这句话是有两个条件的：

条件一：区域1上的点
条件二：将点映射

首先我们先解决第一个条件的问题，即怎么判断哪些点在区域1上面呢？
我们已经知道线段BE的关系式，再根据数学基础知识，我们由图可知在线段BE上方的都是区域1的点，那么可以写出以下判断公式，如果满足该公式：
$$y_1+\frac{\sqrt{3}}{3}{x}_1>0=>\sqrt{3}{y}_1+x_1>0$$
那么，必定在区域1的位置。
即代码中的前半句判断条件if( p.x+k*p.y>0.0 )

我们再分析第二个条件，将点映射，即将所有区域1上的点关于线段BE对称，映射到区域3上。
抽象一下，这里其实演变成了一道数学题，即任意一点关于某直线对称，求另一点。

注：可以参考这里任意一点关于某直线对称的数学原理讲解

我们假设区域1上的任意一点为$P(x,y)$，将该点关于直线$y_1=-\frac{\sqrt{3}}{3}{x}_1$对称，那么点$P^{\prime }（m,n）$应该怎么求得？
如下图所示，我们可以利用解析法，分别按照该步骤即可求得：
（1）两直线垂直，斜率之间的关系：$k_1\ast k_2=-1$
（2）$P{P}^{\prime }$的解析式
（3）交点$G$的坐标
（4）利用中点坐标公式

（1）求取斜率
直线$y_1=-\frac{\sqrt{3}}{3}{x}_1$的斜率为$-\frac{\sqrt{3}}{3}$，根据斜率之间的关系：$k_1\ast k_2=-1$，那么直线$y_2$的斜率即为 $\sqrt{3}$,
得直线方程$P{P}^{\prime }$：
$$y_2=\sqrt{3}{x}_2+b$$

（2）$P{P}^{\prime }$的解析式
这一步我们要求取$b$，我们已知过点$P^{\prime }（x,y）$，那么将点P代入$y_2$直线方程可以求得：
$$b=y-\sqrt{3}x$$
即$P{P}^{\prime }$的解析式为：
$$y_2=\sqrt{3}{x}_2+(y-\sqrt{3}x)$$

（3） 交点$G（j,k）$的坐标
我们已知两直线方程$y_1与y_2$,那么他们之间交点$G$的坐标，可以通过联立方程组求得，将点$G$代入方程组：
$$\{\begin{array}{c}{y}_1=-\frac{\sqrt{3}}{3}{x}_1\\ y_2=\sqrt{3}{x}_2+(y-\sqrt{3}x)\end{array}$$
得：
$$\{\begin{array}{c}k=-\frac{\sqrt{3}}{3}j\\ k=\sqrt{3}j+(y-\sqrt{3}x)\end{array}$$
对其进行加减消元，得：
$$\{\begin{array}{c}j=-\frac{3x-\sqrt{3}y}{4}\\ k=\frac{y-\sqrt{3}x}{4}\end{array}$$
（4）利用中点坐标公式
已知点$P(x,y)$，点$G(j,k)$，求点$P^{\prime }(m,n)$，利用中点坐标公式即可。
$$\{\begin{array}{c}j=\frac{x+m}{2}\\ k=\frac{y+n}{2}\end{array}$$
分别将求得的$j=-\frac{3x-\sqrt{3}y}{4}$,$k=\frac{y-\sqrt{3}x}{4}$，代入上式，最终得：
$$\{\begin{array}{c}m=\frac{x-\sqrt{3}y}{2}\\ n=\frac{-\sqrt{3}x-y}{2}\end{array}$$
即我们成功的求得了$P$点的对称点$P^{\prime }$的坐标值，对应代码：
p=vec2(p.x-k*p.y,-k*p.x-p.y)/2.0
至此我们终于将最难的部分讲解完成了😬😬😬

4、剩余代码

针对于代码4p.x -= r;，即可以理解将区域2与区域4划分出去，将范围缩小为$[-x-r,x-r]$。

针对于代码5p.y += r/k;，由上面我们知道$OD=\frac{\sqrt{3}}{3}$，为了让$y$轴向下移动$\frac{\sqrt{3}}{3}r$个单位，让$[0,-\frac{\sqrt{3}}{3}]$这部分范围全部变为$[\frac{\sqrt{3}}{3},0]$，这样三角形区域的$y$轴部分都是正数了。

针对于代码6p.x -= clamp( p.x, -2.0*r, 0.0 );，我理解是将三角形边缘处变得更加平滑，因为将这句代码注释掉的话其实并不影响，只是边缘处不太平滑。

针对于代码7return -length(p)*sign(p.y);这里为什么要用$y$的正负号确定呢？
因为我们在代码5中将$y$轴下移了，所以三角形上方全部是正号，而我们知道，SDF符号距离场内部应该是负号，所以在整个代码7的前面加上了一个负号，进行取反操作。

各位小伙伴，如果有不明白的地方或者有更好的讲解，欢迎在下方留言评论哦！😁😁😁