【PL理论深化】(1) 数学归纳法：集合的归纳性定义 | 推理规则：前提 / 结论 | 证明规则和证明树 | CFG 上下文无关文法：G = (V, Σ, R, S) | 归纳定义的例子

平渊道人

已于 2024-06-24 06:55:45 修改

阅读量1.6k

点赞数 59

分类专栏： PL理论深化 (Master) 文章标签： PL理论 PL 编程语言理论程序语言理论

于 2024-06-21 07:50:01 首次发布

zdfs

本文链接：https://blog.csdn.net/weixin_50502862/article/details/139724879

版权

PL理论深化 (Master) 专栏收录该内容

4 篇文章 0 订阅

订阅专栏

💬 写在前面：所有编程语言都是通过归纳法定义的。因此，虽然编程语言本身是有限的，但用该语言编写的程序数量是没有限制的，本章将学习编程语言研究中最基本的归纳法。

Ⅰ. 推理规则（IR）

0x00 集合的归纳性定义

0x01 推理规则和公理

0x02 证明规则和证明树（Proof Rule & Proof Tree）

0x03 上下文无关文法 (context-free grammar)

Ⅱ. 归纳定义的例子

0x00 归纳定义 3的倍数集合 {0, 3, 6, 9, ...}

0x01 归纳定义平衡括号（Banlanced parentheses）

0x02 归纳定义字符串集合

0x03 归纳定义所有可能出现的字符串集合

0x04 递归定义构建整数列表的集合

0x05 归纳定义一颗二叉树

Ⅰ. 推理规则（IR）

0x00 集合的归纳性定义

归纳法 (Mathematical Induction, MI) 是利用自身来定义集合的方法。

现在，我们定义集合 $\color{} S$ 为满足以下两个条件的最小自然数集合：

$\color{} S$ 包含 $\color{}0$ ( $\color{}0 \in S$ )
若 $\color{}S$ 包含自然数 $\color{} n$ ( $\color{} n\in \mathbb{N}$ ) ，那么 $\color{} S$ 也包含 $\color{} n+3$ ( $\color{} n \in S \Rightarrow n + 3 \in S$ )

这种定义被称为归纳法的原因是，在定义属于 $\color{} S$ 的元素时，利用了已经属于 $\color{} S$ 的元素。

以这种方式定义的集合 $\color{} S$ 说明了什么？

首先，根据第一个条件，集合 $\color{} S$ 必须包含 0。
如果 $\color{} S$ 包含 0，那么根据第二个条件，它必须包含 3。
同样地，如果 $\color{} S$ 包含 3，那么它必须包含 6。

重复这个过程，可以发现集合 $\color{} S$ 必须包含所有 3 的倍数。

然而，满足这两个条件的集合并不仅限于 3 的倍数：

自然数的整个集合 $\color{} \{ 0, 1, 2, 3, ... \}$ 也满足上述两个条件。
集合 $\color{} \{0, 3, 6, 9, ...\} \cup \{1, 4, 7, 10, ...\}$ 也满足这两个条件。

以这种方式，满足这两个条件的集合可以有无限多。

因此，上述定义中将 $\color{} S$ 定义为满足这两个条件的 "最小集合"，这个集合是 3 的倍数的集合：

$\color{} \{0, 3, 6, 9, ...\}$

3 的倍数的集合满足这两个条件，并且包含在任何满足这两个条件的集合中。

像上述例子一样，集合的归纳定义由两种类型的规则组成。

第一种类型的规则是无条件地规定属于集合的基本元素 ( $\color{} S$ 包含 0 ) 。

第二种类型的规则是利用已经属于集合的元素来定义的新元素。

( 如果 $\color{} S$ 包含某个自然数 $\color{} n$ ，那么 $\color{}S$ 也包含 $\color{} n+3$ )

注意，基本元素必须始终定义明确，因为没有基本元素的归纳定义总是意味着空集 ( $\color{} \varnothing$ )。

0x01 推理规则和公理

我们在对集合进行归纳定义时，会经常使用 推理规则 (inference rule) 。

我们来定义一个逻辑：若 $\color{} A1, A2, ..., An$ 皆为真，那么 $\color{} B$ 也为真，即：

$\color{}{\Big(\bigwedge_{i=1}^{n} A_i \Big) \Rightarrow B}$

推理规则由 前提 + 结论 组成，上述逻辑的推理规则可如下表示 (简写) ：

前提 ( $\color{} A1, A2, ..., An$ ) 和结论 ( $\color{} B$ ) 组成了推理规则。

不包含前提的推理规则称为公理 (axiom)，表示在没有任何条件的情况下，结论为真。

例子：如果用推理规则来定义上述定义的包含 3 的倍数的集合 $S$

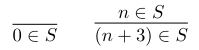
左侧规则：无任何条件的情况下，命题 $\color{} 0\in S$ 是事实，即集合 $\color{} S$ 包含自然数 0
右侧规则：如果集合 $\color{} S$ 包含某个自然数 $\color{} n$ ，则它必须包含自然数 $\color{} n+3$

0x02 证明规则和证明树（Proof Rule & Proof Tree）

推理规则定义了满足这两个条件的最小集合，尽管并未明确规定 "最小集合" 的条件。

将推理规则视为 证明规则 (proof rule)，可以更清晰地解释其含义。

使用上述推理规则定义集合 $\color{} S$ ，作为能够证明命题 $\color{} n\in S$ 的自然数 $\color{} n$ 的集合。

例如，如果 $\color{} S$ 包含自然数 6，那是因为可以证明命题 $\color{} 6\in S$ ，如下所示：

证明是从公理对应的规则开始，通过反复应用推理规则直到推导出所要证明的命题的过程。

这样的证明过程也被称为 证明树 (proof tree) ，这是一颗再简单不过的证明树了。

在上述例子中，首先利用公理推导出命题 $\color{} 0\in S$ ，然后再应用右侧规则两次推导出 $\color{} 6\in S$ 。

因此，像 $\color{} 0 \in S, 3 \in S, 6 \in S, 9 \in S, ...$ 这样的命题都是 可证的 (provable)。

所以上述推理规则定义的集合包含所有的 3 的倍数：

$\color{} S = \{ 3k \mid k \in \{0, 1, 2, 3, \ldots\} \}$

相反，像 $\color{} 1\in S$ 或者 $\color{} 4\in S$ 这样的命题是不可证的，因此它们不属于集合 $S$ 。

因此，集合 $\color{} S$ 正好包含所有的 3 的倍数。当将推理规则解释为证明规则来定义时，

并不需要额外考虑 "最小集合" 的条件，因为它根据规则是包含所有闭合集合中最小的集合。

为了表达简洁，通常在通过推理规则来定义集合时，省略当前正在定义的集合。

例如，上述推理规则可以这么写：

0x03 上下文无关文法 (context-free grammar)

上下文无关文法 (context-free grammar)，简称 CFG，由一个四元组构成：

$\color{}{\mathbb G = \Big(\mathbb V, \Sigma, \mathbb R, \mathbb S\Big)}$

$\color{}V$ 表示一组非终结符号 (Variable, 变量)
$\color{} \Sigma$ 表示一组终结符号 (End, 结束)
$\color{} R$ 表示一组产生式规则 (Rule, 规则)
$\color{}S$ 表示起始符号 (Start, 开始)

比如，初始情况下 $\color{}S$ 可以生成 0，表示集合中的基础元素。

递归情况下，如果 $\color{}S$ 可以生成某个元素 $\color{} x$ ，那么 $\color{}S$ 也可以生成 $\color{} 2x+1$ 。

这意味着，从基础元素 0 开始，应用规则 $\color{} S \rightarrow 2S + 1$ 可以生成 1, 3, 7, 15 等等。

通过应用这些规则，我们可以生成集合中的元素：

$\color{} S \rightarrow 0 \) , \( S \rightarrow 2S + 1$

如果 $\color{} S \rightarrow 0$ ，则 $\color{} 2S + 1 \rightarrow 2 \cdot 0 + 1 = 1$

如果 $\color{} S \rightarrow 1$ ，则 $\color{} 2S + 1 \rightarrow 2 \cdot 1 + 1 = 3$

如果 $\color{} S \rightarrow 3$ ，则 $\color{} 2S + 1 \rightarrow 2 \cdot 3 + 1 = 7$

……

以此类推，可得 $\color{} 0, 1, 3, 7, 15, \ldots$

推理规则有时候也会利用上下文无关文法来进行表达：

$\color{} n\rightarrow 0\, |\, n+3$

所欲定义的集合以 0 为基础元素，并且若该集合包含 $\color{} n$ ，则必须包含 $\color{} n+3$ 。

同样，省略掉最小集合的条件。

Ⅱ. 归纳定义的例子

0x00 归纳定义 3 的倍数集合 {0, 3, 6, 9, ...}

让我们来看一些通过归纳定义的集合的例子。

以下推理规则也定义了 3 的倍数集合 $\color{} \{0, 3, 6, 9, ...\}$

规则一 & 规则二：表示集合以基本元素 0 和 3 为起点
规则三：如果 $\color{} x$ 和 $\color{} y$ 是集合的元素，则 $\color{} x+y$ 也是元素

0x01 归纳定义平衡括号（Banlanced parentheses）

平衡括号 (Banlanced parentheses) ，指的是括号的使用符合特定规则，

使得每个左括号 ( 都有对应的右括号 ) ，并且它们之间的顺序正确。

例如，表达式 ((())) 和 ()() 是平衡括号，因为每个左括号都有匹配的右括号，并且括号的嵌套顺序是正确的。
一些常见的方法来检查括号是否平衡包括使用栈数据结构。可以按顺序遍历字符串，并将遇到的每个左括号压入栈中，当遇到右括号时，从栈中弹出一个左括号，以检查是否匹配。如果字符串遍历结束时栈为空，则说明括号是平衡的；否则，括号不平衡。

括号匹配的字符串的集合。根据这样的推理规则定义集合：

可以用如下推理规则来定义：

规则一：指出空字符串 () 属于集合 $\color{} S$ 。
规则二：如果某个字符串 $\color{} s$ 属于集合 $\color{} S$ ，则 (s) 也属于集合 $\color{} S$ 。
规则三：如果字符串 $\color{} s_1,s_2$ 都属于集合 $\color{} S$ ，则它们的连接 $\color{} s_1s_2$ 也属于集合 $\color{} S$ 。

例如，字符串 (()()) 可以按照以下方式构造：

在每个证明的步骤中说明了应用了哪些推理规则。

0x02 归纳定义字符串集合

让我们定义集合 $\color{} S$ ，其中 $\mathbb{N}$ 表示所有自然数的集合：

$\color{} x^n$ 表示如下定义的字符串， $\color{} \epsilon$ 表示长度为 0 的空字符串：

根据以上集合 $\color{} S=\{b,abb,aabbb,aaabbbb,...\}$ ，我们可以将其定义成如下推理规则：

规则一：字符串 $\color{} b\in S$
规则二：如果集合 $\color{} S$ 包含字符串 $\color{} s$ ，则字符串 $\color{} asb$ 也属于该集合

0x03 归纳定义所有可能出现的字符串集合

有英文字母集合 $\color{} \Sigma =\{a,...z\}$ ，

可以定义如下的推理规则来构建所有可能出现的字符串集合：

可以通过在推理规则的右侧添加条件来简洁地表示多个形式相同的规则 (规则一除外) ：

当字符串 $\color{} s\in \Sigma$ ，并且 $\color{} x$ 是任意的英文字母时，字符串 $\color{} xs$ 也属于该集合。

通过语法来定义相同的集合如下：

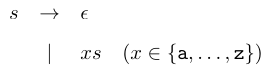
0x04 递归定义构建整数列表的集合

由整数作为元素的列表的集合，可以这么定义：

规则一：空列表是整数列表 ( $\color{} nil\in l_\mathbb{Z}$ )
规则二：如果 $l$ 是整数列表，则在其前面添加一个整数形成的列表 $\color{} (n\cdot i)$ 也是整数列表。

例如 $\color{} -7\cdot 3 \cdot14 \cdot nil$ 就是通过上述规则生成的列表。

因此，可以从公理开始，反复利用 推理规则 来生成它：

上述列表用语法形式的定义如下：

这个例子说明了如何通过递归定义来构建整数列表的集合。

列表可以是空列表 ( $\color{} nil$ )，也可以是一个整数加上另一个整数列表。

通过这两条规则，就可以逐步构造出包含整数的复杂列表。

0x05 归纳定义一颗二叉树

下面是一颗普通到不能再普通的二叉树 (binary tree)：

每次都用图形来表示树的结构着实很麻烦，所以我们可以这样来表示上述的二叉树：

下面我们将经常用这种括号的方式来表示具有二维结构的数据。

像上述那样形成的二叉树集合可以通过以下归纳规则定义：

规则一：定义了只包含一个叶节点 (leaf) 的空二叉树
规则二：定义了当有两棵二叉树 $\color{} t_1$ 和 $\color{} t_2$ 时，可以以整数 $\color{} n$ 作为根节点，将 $\color{} t_1$ 和 $\color{} t_2$ 分别作为左子树和右子树，从而创建一个新的二叉树 ( $\color{} n,t_1,t_2$ )

举个例子，根据上述规则，二叉树：

可以用以下推理规则证明：

下面，我们来定义一棵另一种风格的二叉树。

考虑将数据存储在叶子节点而不是内部节点的二叉树，如下所示：

在这里， $\color{} nil$ 表示该分支没有子节点，假设我们用括号在一维中表示树。

如 1、(1, nil)、((1, 2), nil)、((1, 2), (3, 4)) ，我们可以归纳地定义一组二叉树如下：

举个例子，((1, 2),(3, nil)) 将被创建如下：

📌 [ 笔者 ]   王亦优
📃 [ 更新 ]   2024.6.21
❌ [ 勘误 ]   /* 暂无 */
📜 [ 声明 ]   由于作者水平有限，本文有错误和不准确之处在所难免，
              本人也很想知道这些错误，恳望读者批评指正！

📜 参考资料

- R. Neapolitan, Foundations of Algorithms (5th ed.), Jones & Bartlett, 2015.

- T. Cormen《算法导论》（第三版），麻省理工学院出版社，2009年。

- T. Roughgarden, Algorithms Illuminated, Part 1~3, Soundlikeyourself Publishing, 2018.

- J. Kleinberg&E. Tardos, Algorithm Design, Addison Wesley, 2005.

- R. Sedgewick&K. Wayne，《算法》（第四版），Addison-Wesley，2011

- S. Dasgupta，《算法》，McGraw-Hill教育出版社，2006。

- S. Baase&A. Van Gelder, Computer Algorithms: 设计与分析简介》，Addison Wesley，2000。

- E. Horowitz，《C语言中的数据结构基础》，计算机科学出版社，1993

- S. Skiena, The Algorithm Design Manual (2nd ed.), Springer, 2008.

- A. Aho, J. Hopcroft, and J. Ullman, Design and Analysis of Algorithms, Addison-Wesley, 1974.

- M. Weiss, Data Structure and Algorithm Analysis in C (2nd ed.), Pearson, 1997.

- A. Levitin, Introduction to the Design and Analysis of Algorithms, Addison Wesley, 2003. - A. Aho, J. Hopcroft, and J. Ullman, Data Structures and Algorithms, Addison-Wesley, 1983.

- E. Horowitz, S. Sahni and S. Rajasekaran, Computer Algorithms/C++, Computer Science Press, 1997.

- R. Sedgewick, Algorithms in C: 第1-4部分（第三版），Addison-Wesley，1998

- R. Sedgewick，《C语言中的算法》。第5部分（第3版），Addison-Wesley，2002

平渊道人

关注

59
点赞
踩
14

收藏

觉得还不错? 一键收藏
打赏
6
评论
【PL理论深化】(1) 数学归纳法：集合的归纳性定义 | 推理规则：前提 / 结论 | 证明规则和证明树 | CFG 上下文无关文法：G = (V, Σ, R, S) | 归纳定义的例子

所有编程语言都是通过归纳法定义的。因此，虽然编程语言本身是有限的，但用该语言编写的程序数量是没有限制的，本章将学习编程语言研究中最基本的归纳法。
复制链接

扫一扫