第一张主要讲了线性规划问题,并介绍了两种求解方法:
图解法、单纯形法
对于以后期末复习
- 知道单纯性表法和两阶段法的区别
- 知道单纯形表的几种情况【唯一解、多解、无解】
- 会算检验数
-
弄清楚基本解可行解最优解退化解
线性规划
指在一定的线性约束条件下,求一个线性函数的极值问题
写在前面:名词解释及关系
线性规划(LP)问题
min
S
=
C
X
s. t.
{
A
X
=
b
X
⩾
0
\begin{array}{c} \min S=\boldsymbol{C} \boldsymbol{X} \\ \text { s. t. }\left\{\begin{array}{l} \boldsymbol{A} \boldsymbol{X}=\boldsymbol{b} \\ \boldsymbol{X} \geqslant \boldsymbol{0} \end{array}\right. \end{array}
minS=CX s. t. {AX=bX⩾0
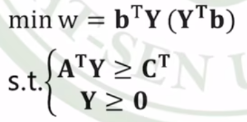
min对应
⩾
\geqslant
⩾【在第一章好像还没找到对应的部分,但是做题是这样的】
可用这一向量形式表示的问题
可行解
满足上述线性规划问题条件的所有解 X \boldsymbol X X
最优解
可行解中满足条件 min S = C X \min S=\boldsymbol{C} \boldsymbol{X} minS=CX的解
基本解

在2.2中
X
=
(
B
−
1
b
0
)
X=\left(\begin{array}{l} B^{-1}b \\ 0\end{array}\right)
X=(B−1b0)是基
B
B
B的基本解
可行基/基本可行解
若 B − 1 b ⩾ 0 B^{-1}b\geqslant 0 B−1b⩾0,则称 B B B为可行基, X = ( B − 1 b 0 ) X=\left(\begin{array}{l} B^{-1}b \\ 0\end{array}\right) X=(B−1b0)为基本可行解
定理:基本解与基本可行解
若X中非零分量所对应的列向量线性无关,则 X是(LP) 的一个基本可行解
最优基/最优基本可行解
若 B − 1 b ⩾ 0 B^{-1}b\geqslant 0 B−1b⩾0且 C − C B B − 1 A ⩾ 0 C-C_BB^{-1}A\geqslant0 C−CBB−1A⩾0,则称 B B B为最优基, X = ( B − 1 b 0 ) X=\left(\begin{array}{l} B^{-1}b \\ 0\end{array}\right) X=(B−1b0)为最优基本可行解
最优性判别定理


退化/非退化基本可行解
若
B
−
1
b
B^{-1}b
B−1b中至少有一个分量为 0,则称该基本可行解为退化基本可行解。
例如:
凸组合
设 X 1 , X 2 , ⋯ , X k \boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \cdots, \boldsymbol{X}_{k} X1,X2,⋯,Xk 是 R n \mathbf{R}^{n} Rn 中已知的 k k k 个点, 若对于某点 X ∈ R n \boldsymbol{X} \in \mathbf{R}^{n} X∈Rn , 存在非负常数 λ 1 , λ 2 , ⋯ , λ k \lambda_{1}, \lambda_{2}, \cdots, \lambda_{k} λ1,λ2,⋯,λk , 使得
X = ∑ i = 1 k λ i X i , 且 ∑ i = 1 k λ i = 1 \boldsymbol{X}=\sum_{i=1}^{k} \lambda_{i} \boldsymbol{X}_{i}, \quad \text { 且 } \sum_{i=1}^{k} \lambda_{i}=1 X=i=1∑kλiXi, 且 i=1∑kλi=1
则称 X \boldsymbol{X} X 是 X 1 , X 2 , ⋯ , X k \boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \cdots, \boldsymbol{X}_{k} X1,X2,⋯,Xk 的凸组合.

凸集


极点
设 X \boldsymbol{X} X是凸集 D D D中的一点,如果 X \boldsymbol{X} X不能表示为 D D D中两个相异点的凸组合,则 X \boldsymbol{X} X称为 D D D的极点.
如:多面体极点,球体球面上的点。
定理:极点与基本可行解
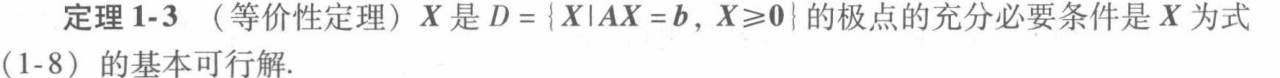
典式
对于每一个基本可行解,线性规划问题都有一个典式。
按照2.2的推导过程,可得到典式

按照上述方法展开,可以得到典式的另一种表达形式:

注意细节:表达规范,如max/min
典式指的应该就是,能找出一组单位向量【与列向量数目相同】的式子?】
单纯形表
按照上面的【展开后的】典式表达,单纯形表长这样:

其中第0行的-S因为在迭代中不会变化,因此省略
注意做题规范
应当保证单纯性表中的基向量第零行对应系数为0,若不为0,需要进行行间的加减操作。
同时应该保证第
i
i
i行的基向量
x
j
x_j
xj所对应列只有第
i
i
i个数为1,其他为0
c
j
c_j
cj是第零行
x
j
x_j
xj对应系数。
1 线性规划的标准形式
min S = c 1 x 1 + c 2 x 2 + ⋯ + c n x n s. t. { a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋮ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m x 1 ⩾ 0 , x 2 ⩾ 0 , ⋯ , x n ⩾ 0 \begin{array}{c} \min S=c_{1} x_{1}+c_{2} x_{2}+\cdots+c_{n} x_{n} \\ \text { s. t. }\left\{\begin{array}{c} a_{11} x_{1}+a_{12} x_{2}+\cdots+a_{1 n} x_{n}=b_{1} \\ a_{21} x_{1}+a_{22} x_{2}+\cdots+a_{2 n} x_{n}=b_{2} \\ \vdots \\ a_{m 1} x_{1}+a_{m 2} x_{2}+\cdots+a_{m n} x_{n}=b_{m} \\ x_{1} \geqslant 0, x_{2} \geqslant 0, \cdots, x_{n} \geqslant 0 \end{array}\right. \end{array} minS=c1x1+c2x2+⋯+cnxn s. t. ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋮am1x1+am2x2+⋯+amnxn=bmx1⩾0,x2⩾0,⋯,xn⩾0
式中
b
i
,
c
j
,
a
i
j
b_{i}, c_{j}, a_{i j}
bi,cj,aij为实常数, 且
b
i
⩾
0
b_{i} \geqslant 0
bi⩾0 ;
x
j
x_{j}
xj 一一要求的一组变量.
写成向量形式,有
min
S
=
C
X
s. t.
{
A
X
=
b
X
⩾
0
\begin{array}{c} \min S=\boldsymbol{C} \boldsymbol{X} \\ \text { s. t. }\left\{\begin{array}{l} \boldsymbol{A} \boldsymbol{X}=\boldsymbol{b} \\ \boldsymbol{X} \geqslant \boldsymbol{0} \end{array}\right. \end{array}
minS=CX s. t. {AX=bX⩾0
为了将线性约束转为标准形式,需要进行一些转换,如:
- 将求极大转化为求极小:取负号
- 将不等式转化为等式:引入松弛变量
y
i
⩾
0
y_i\geqslant 0
yi⩾0;剩余变量
y
l
⩾
0
y_l\geqslant 0
yl⩾0
-
大于等于
a i 1 x 1 + a i 2 x 2 + ⋯ + a i n x n ⩽ b i a_{i 1} x_{1}+a_{i 2} x_{2}+\cdots+a_{i n} x_{n} \leqslant b_{i} ai1x1+ai2x2+⋯+ainxn⩽bi
化为
a i 1 x 1 + a i 2 x 2 + ⋯ + a i n x n + y i = b i a_{i 1} x_{1}+a_{i 2} x_{2}+\cdots+a_{i n} x_{n}+y_{i}=b_{i} ai1x1+ai2x2+⋯+ainxn+yi=bi -
小于等于
a l 1 x 1 + a l 2 x 2 + ⋯ + a l n x n ⩾ b l a_{l 1} x_{1}+a_{l 2} x_{2}+\cdots+a_{l n} x_{n} \geqslant b_{l} al1x1+al2x2+⋯+alnxn⩾bl
化为
a l 1 x 1 + a l 2 x 2 + ⋯ + a l n x n − y l = b l a_{l 1} x_{1}+a_{l 2} x_{2}+\cdots+a_{l n} x_{n}-y_{l}=b_{l} al1x1+al2x2+⋯+alnxn−yl=bl
-
- 将自由变量化为非负变量
如某个变量 x k x_k xk没有大小要求,则称之为自由变量,用两个非负变量相减代替之
x k = x k ′ − x k ′ ′ , x k ′ ⩾ 0 , x k ′ ′ ⩾ 0 x_k=x_k'-x_k'',x_k'\geqslant0,x_k''\geqslant0 xk=xk′−xk′′,xk′⩾0,xk′′⩾0
2 线性规划问题的求解
在以后的讨论中,我们都假定 A A A的秩为m (自然m≤n).我们从 A A A的n列中选出m个线性无关的列组成一个m阶矩阵。【为了表达方便起见,假定选择的是 A A A的前m列,并且用 B B B表示这个矩阵,于是 B B B是非奇异的,称为(LP)的一个基】
2.1 分解约束条件
令

重写线性规划问题,有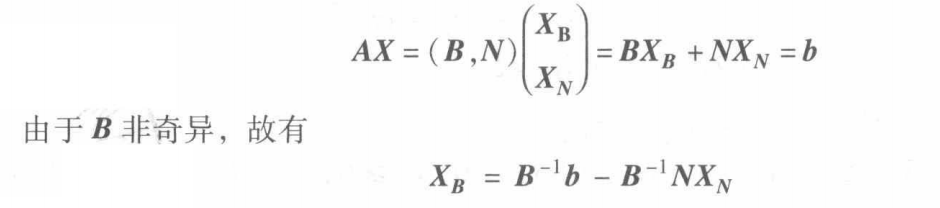

【非基
X
N
X_N
XN可以用基
X
B
X_B
XB表示因此可令其为0,基不唯一】
2.1.1 定义

定义见上方
2.2 分解目标函数
相对应的对
C
C
C进行分解,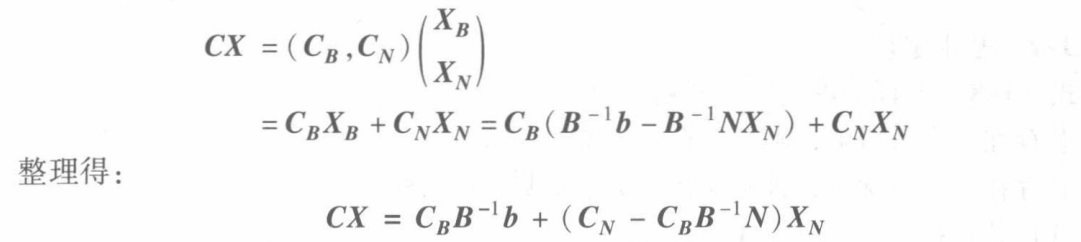
2.2.1 定义 最优基

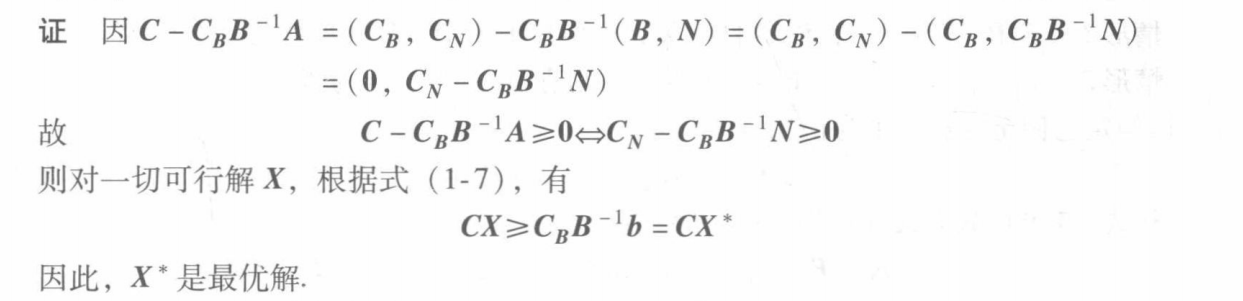
注意这里的等效
2.3 概念区分

3 图解法及集合理论
3.1 解法
高中知识,略
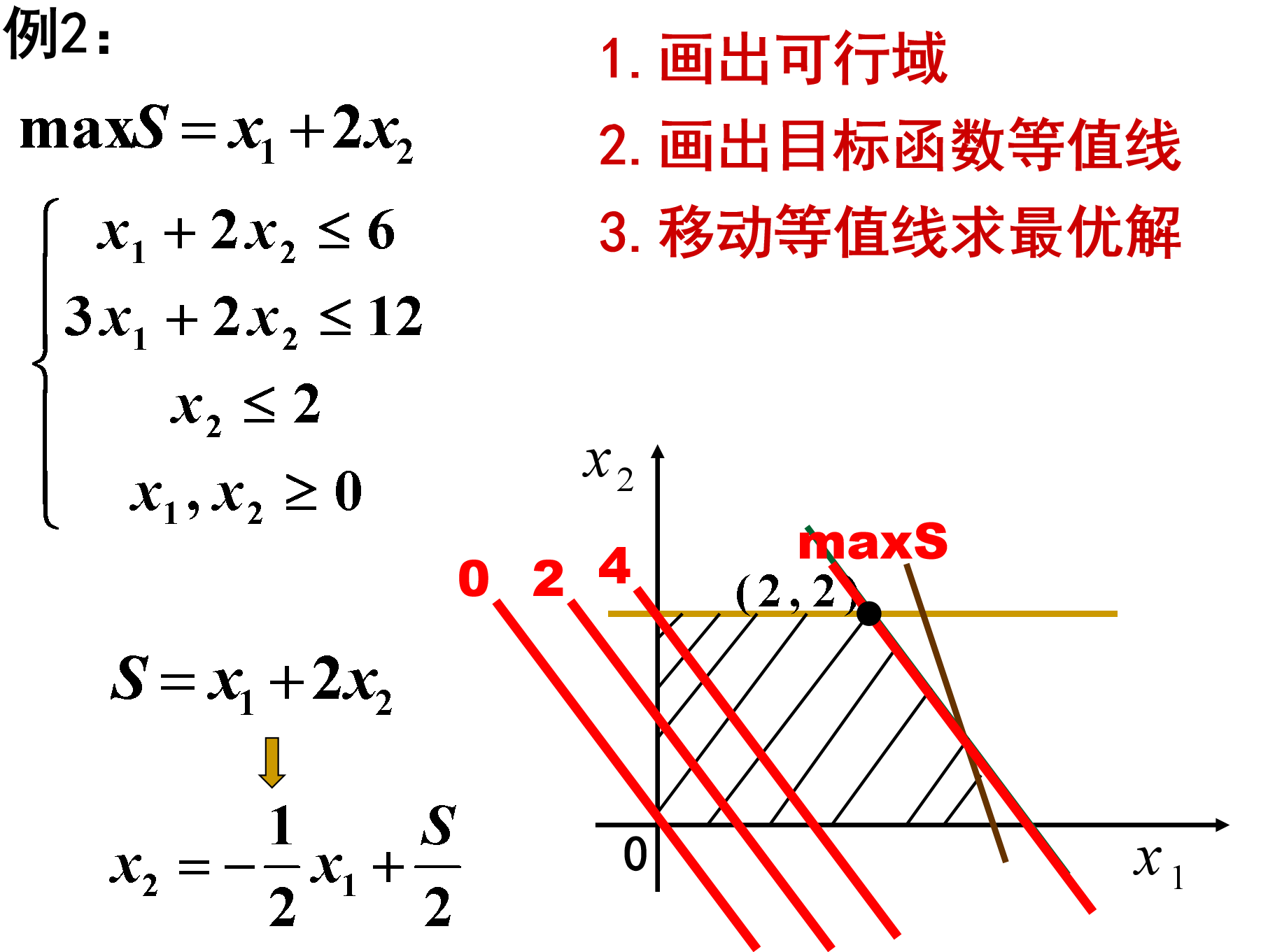
3.2 几何理论
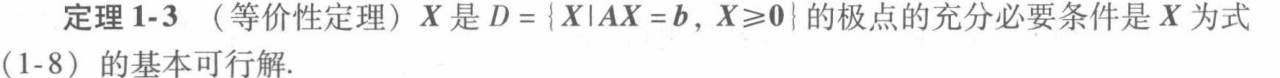 推论1 若凸集 D={X|AX=b,x>0}非空,则它至少有一个极点.
推论1 若凸集 D={X|AX=b,x>0}非空,则它至少有一个极点.
推论2 如果一个线性规划问题有有限的最优解,则必有一个最优解是 D的极点

Q:极点和顶点的区别?
Q:线性规划问题的任一可行解都可以用全部基可行解的线性组合表示 这句话为什么错了
根据定理1—4,X可以由凸集顶点的凸组合表示,那更能被基可行解线性表示吧
4 单纯形法

线性规划问题的目标函数的最小值(或最大值) 一定在基本可行解(即极点)上达到。所以,在寻找最优解时,只需要考虑基本可行解就够了。
单纯形法的基本思想是从一个基本可行解出发,转移到另一个目标函数值更小的基本可行解
如此逐次转移下去,当目标函数值不能再减小,即满足最优性条件:
C
−
C
B
B
−
1
A
≥
0
C-C_BB^{-1}A≥0
C−CBB−1A≥0时,计算结束,得到最优基本可行解。
4.1 求一个可行解
4.2 从可行解迭代求出最优解
迭代原理【方法的关键,有助于理解】
由最优性判别原理,
(1) 若
y
0
j
⩾
0
,
j
=
m
+
1
,
⋯
,
n
y_{0 j} \geqslant 0, j=m+1, \cdots, n
y0j⩾0,j=m+1,⋯,n 根据最优性判别定理,
X
0
\boldsymbol{X}^{0}
X0 是最优解.
(2) 若有某些检验数
y
0
j
y_{0 j}
y0j 是负的, 例如设
y
0
q
<
0
,
m
+
1
⩽
q
⩽
n
y_{0q}<0, m+1 \leqslant q \leqslant n
y0q<0,m+1⩽q⩽n,这时
X
0
\boldsymbol{X}^{0}
X0 不是最优解.
因为此时还可以下降
【1-17】在上面的“典式”的定义中
✨✨✨迭代方法:进基、换基、出基
检验数【检验
X
0
X^0
X0是不是最优解】:若
C
−
C
B
B
−
1
A
≥
0
C-C_{B} B^{-1} A \geq 0
C−CBB−1A≥0 或
C
N
−
C
B
B
−
1
N
≥
0
C_{N}-C_{B} B^{-1} N \geq 0
CN−CBB−1N≥0 ,
即非基变量
x
j
x_{j}
xj 的检验数
y
0
j
=
c
j
−
C
B
B
−
1
p
j
y_{0 j}=c_{j}-C_{B} B^{-1} p_{j}
y0j=cj−CBB−1pj 都
≥
0
\geq 0
≥0, 则
X
0
X^{0}
X0 是最优解。
——也就是说,如果有一个检验数
y
0
j
<
0
y_{0 j}<0
y0j<0的话,这个检验数就具备了“出基”的条件
,如果有不止一个负检验数,则有两种方法确定进基变量:
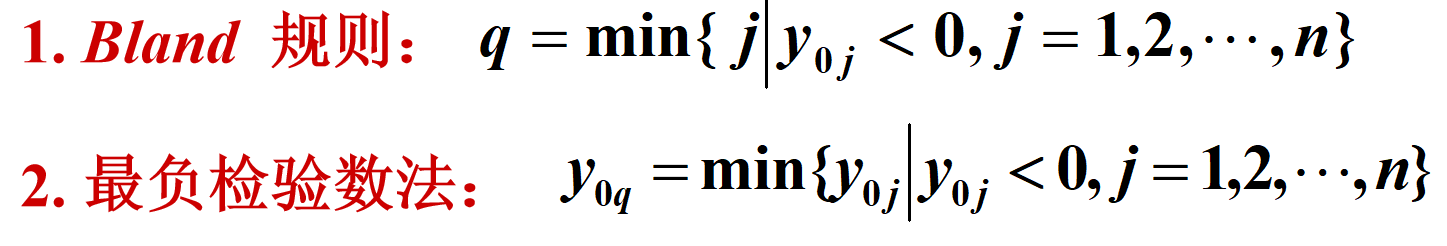
翻译翻译就是:采用Bland规则,算出来的检验数中,最负的
y
0
q
y_{0q}
y0q对应的那一列
x
q
x_q
xq进基。
问题
请结合做题时检验数的求解,说人话:比如检验数怎么算,多个负检验数时怎么办
一般检验数不会写在单纯性表里,而是写在草稿纸上。。。。吗???
进基:接上文, x q x_{q} xq 由非基变量变为基变量。
出基:同时原基变量中必有一个 x i x_i xi从取值为 1 的基变量变为取值为 0 的非基变量
选取方式:求出最小比值
x
q
=
y
p
0
/
y
p
q
x_{q}=y_{p 0} / y_{p q}
xq=yp0/ypq 所在行。原基变量
x
p
x_{p}
xp 变为
0
0
0 , 有三种情况:
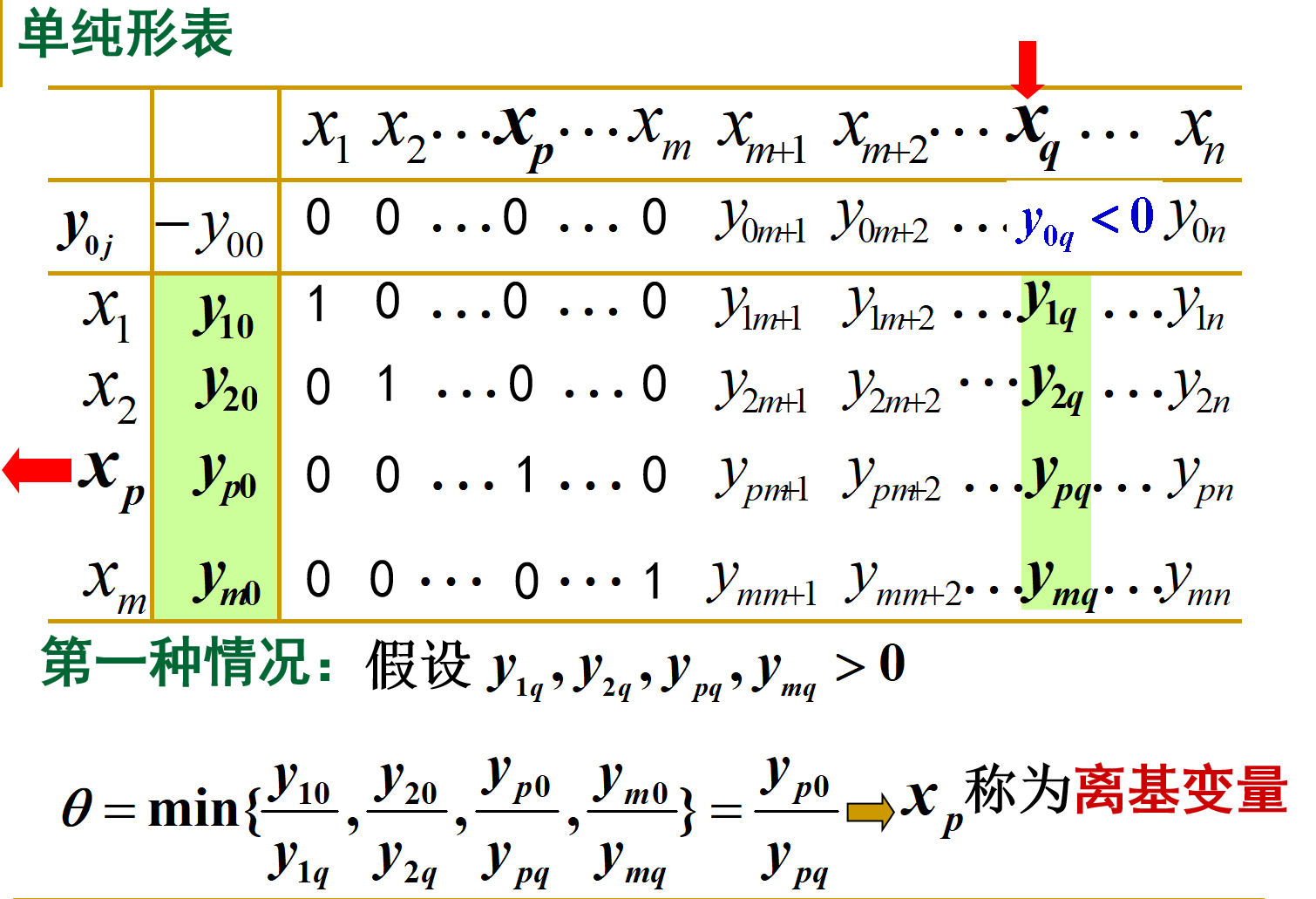

第三种情况:无穷多最优解

换基:在这种情况下,由 负检验数
y
0
q
y_{0q}
y0q 所对应的非基变量
x
q
x_q
xq代替原基变量
x
p
x_p
xp 成为新的基变量。
此时新基变量系数为1,检验数为0【第p列只有一个位置是1,其他都是0】
通过行加减实现
4.3 两阶段法
Q: 何时使用两阶段法?
A: 取决于标准型是不是典式

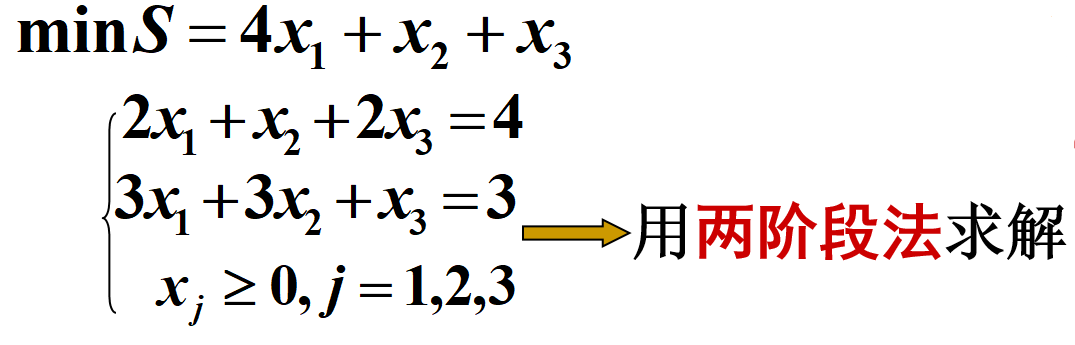
第一阶段
建立辅助(LP),求出原(LP)的一个初始基本可行解。
具体方法:加入m个人工变量,手动变成典式,然后用单纯形法求解
例如:
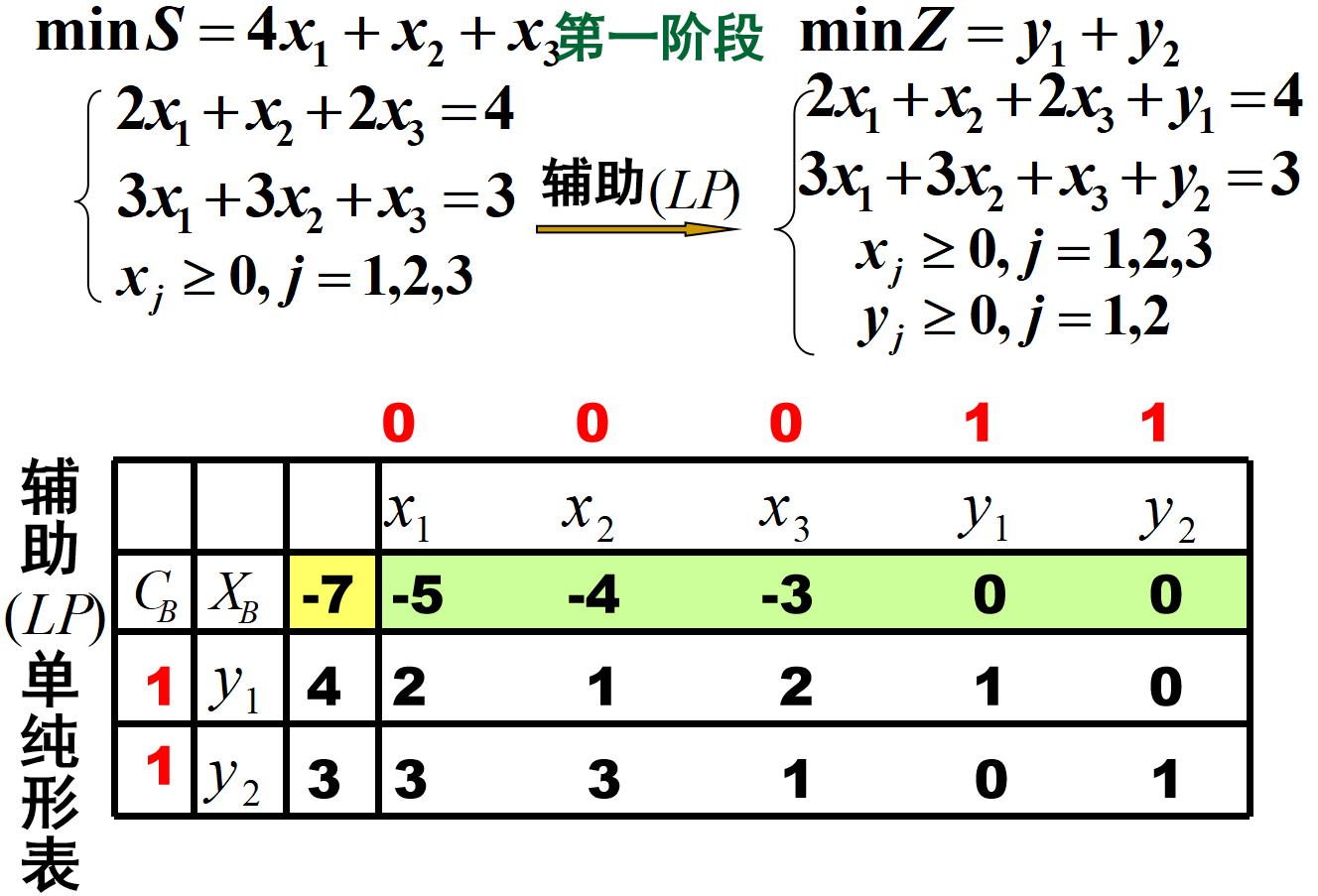
注意,加入了
y
i
y_i
yi变量,并且求的值变成了y的求和的最小值
辅助(LP)的最优解与原(LP)的初始基本可行解的关系:
-
若
Z
∗
=
∑
i
=
1
m
y
i
∗
>
0
, 则原
(
L
P
)
无可行解。
\text { 若 } Z^{*}=\sum_{i=1}^{m} y_{i}^{*}>0 \text {, 则原 }(L P) \text { 无可行解。 }
若 Z∗=∑i=1myi∗>0, 则原 (LP) 无可行解。
证明

-
若
Z
∗
=
∑
i
=
1
m
y
i
∗
=
0
, 则原
(
L
P
)
有一个初始基本可行解。
\text { 若 } Z^{*}=\sum_{i=1}^{m} y_{i}^{*}=0 \text {, 则原 }(L P) \text { 有一个初始基本可行解。 }
若 Z∗=∑i=1myi∗=0, 则原 (LP) 有一个初始基本可行解。
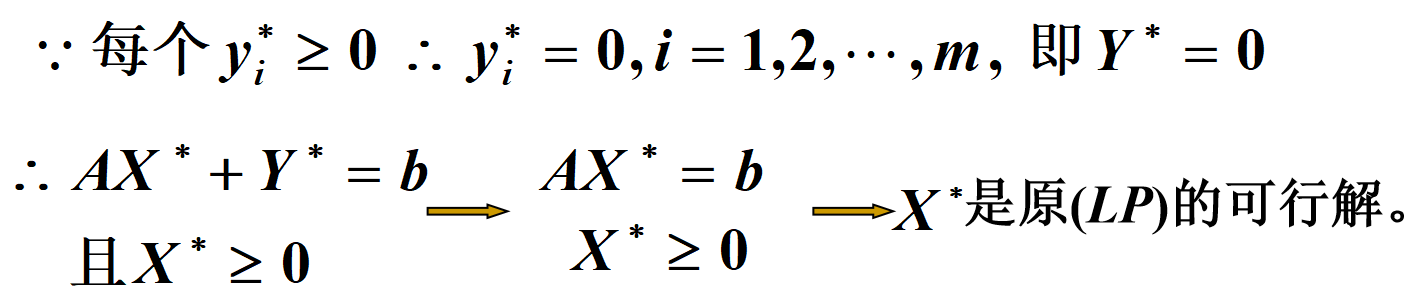
所以在最后做题时,每一步单纯形法要让一个y作为出基变量,有几个y至少迭代几轮。
做题方法


这样,我们最终得到了一个基本可行解 X ∗ X^* X∗
第二阶段
结合上一步得到的基本可行解 X ∗ X^* X∗,再用单纯形法去求原LP的最优解
问题
这一步具体是怎么样的?在单纯表中是怎么用上的基本可行解的
——在辅助 (LP) 的最优表中删去人工列及检验数行
补上原 (LP)的检验数行
Q:怎么补,检验数行怎么求【跟上一个问题重复了】
问题
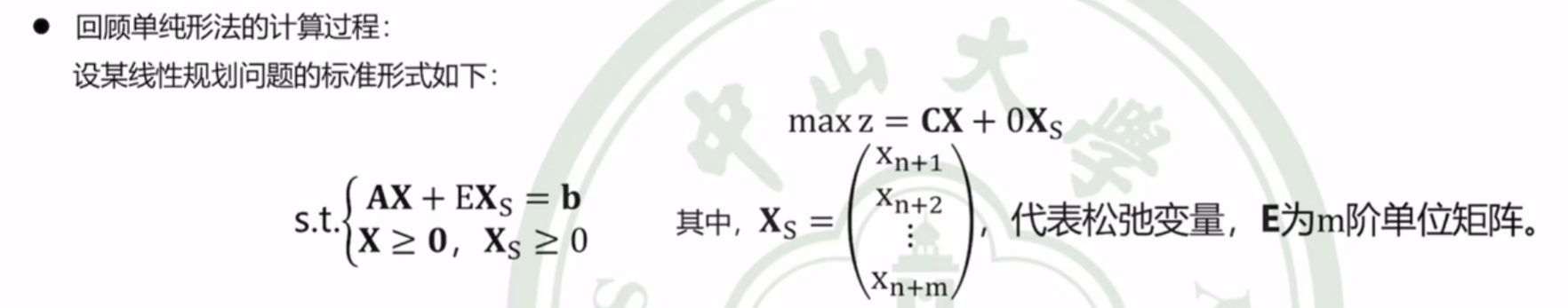
在第二章看到了这个式子,线性规划的标准型是什么样的?
单纯形法应试
必看好题
1-6(1)【无穷情况】;1-6(3)【 y 0 j y_{0j} y0j的确定,记得常数项也要带上,【由于要放到等式另一边,带上负号】,基变量的价值一定是0!】 1-7(3)
标准化
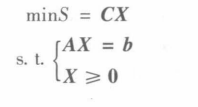
可以用
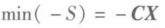
- 形式
max z = ∑ j = 1 n c j x j s.t. { ∑ j = 1 n a i j x j = b i x j ≥ 0 0 ( i = 1 , 2 , … , m ) \begin{array}{l} \max z=\sum_{j=1}^{n} c_{j} x_{j} \\ \text { s.t. }\left\{\begin{array}{l} \sum_{j=1}^{n} a_{i j} x_{j}=b_{i} \\ x_{j} \geq 0 \\ 0 \end{array} \quad(i=1,2, \ldots, m)\right. \end{array} maxz=∑j=1ncjxj s.t. ⎩ ⎨ ⎧∑j=1naijxj=bixj≥00(i=1,2,…,m)
如:
min z = x 1 + 2 x 2 + 3 x 3 s.t. { − 2 x 1 + x 2 + x 3 ≤ 9 − 3 x 1 + x 2 + 2 x 3 ≥ 4 4 x 1 − 2 x 2 − 3 x 3 = − 6 x 1 ≤ 0 , x 2 ≥ 0 , x 3 取值无约束 \begin{array}{l} \min z=x_{1}+2 x_{2}+3 x_{3} \\ \text { s.t. }\left\{\begin{array}{l} -2 x_{1}+x_{2}+x_{3} \leq 9 \\ -3 x_{1}+x_{2}+2 x_{3} \geq 4 \\ \quad 4 x_{1}-2 x_{2}-3 x_{3}=-6 \\ x_{1} \leq 0, x_{2} \geq 0, \quad x_{3} \text { 取值无约束 } \end{array}\right. \end{array} minz=x1+2x2+3x3 s.t. ⎩ ⎨ ⎧−2x1+x2+x3≤9−3x1+x2+2x3≥44x1−2x2−3x3=−6x1≤0,x2≥0,x3 取值无约束
标准化之后:
max z ′ = x 1 ′ − 2 x 2 − 3 x 3 ′ + 3 x 3 ′ ′ + 0 x 4 + 0 x 5 s.t. { 2 x 1 ′ + x 2 + x 3 ′ − x 3 ′ ′ + x 4 = 9 3 x 1 ′ + x 2 + 2 x 3 ′ − 2 x 3 ′ ′ − x 5 = 4 4 x 1 ′ + 2 x 2 + 3 x 3 ′ − 3 x 3 ′ ′ = 6 x 1 ′ , x 2 , x 3 ′ , x 3 ′ ′ , x 4 , x 5 ≥ 0 \begin{array}{l} \max z^{\prime}=x_{1}^{\prime}-2 x_{2}-3 x_{3}^{\prime}+3 x_{3}^{\prime \prime}+0 x_{4}+0 x_{5} \\ \text { s.t. }\left\{\begin{array}{l} 2 \mathrm{x}_{1}^{\prime}+\mathrm{x}_{2}+\mathrm{x}_{3}^{\prime}-\mathrm{x}_{3}^{\prime \prime}+\mathrm{x}_{4}=9 \\ 3 x_{1}^{\prime}+x_{2}+2 x_{3}^{\prime}-2 x_{3}^{\prime \prime}-x_{5}=4 \\ 4 \mathrm{x}_{1}^{\prime}+2 \mathrm{x}_{2}+3 \mathrm{x}_{3}^{\prime}-3 \mathrm{x}_{3}^{\prime \prime}=6 \\ \mathrm{x}_{1}^{\prime}, \mathrm{x}_{2}, \mathrm{x}_{3}^{\prime}, x_{3}^{\prime \prime}, x_{4}, x_{5} \geq 0 \end{array}\right. \end{array} maxz′=x1′−2x2−3x3′+3x3′′+0x4+0x5 s.t. ⎩ ⎨ ⎧2x1′+x2+x3′−x3′′+x4=93x1′+x2+2x3′−2x3′′−x5=44x1′+2x2+3x3′−3x3′′=6x1′,x2,x3′,x3′′,x4,x5≥0
单纯形法
说理解:找到初始基可行解,验证是否最优。验证方法是判断检验数是否全为非正。
若检验数有正数,说明选择该变量可以使系统价值增加【价值比当前基变量组合要高】,选择最大的检验数。这一过程确定了入基变量
为了确定出基变量,判断“对于每一行,如果新入基变量与此行原基变量替换,能换走几个原基变量,选择换的最少的【要求是正数】”【原因是:把出基变量确定为第一个消耗到零的原基变量】
对偶问题列出

- 确定对偶问题中变量的个数m
原大括号中约束条件的个数m等于对偶问题中的变量个数 - 确定对偶问题中的目标函数

- 确定对偶条件中约束条件的个数n
即为原问题变量个数 - 确定对偶问题中约束条件左边部分

【即转置】 - 对偶问题中约束条件右边常数
即原问题中目标函数中 x i x_i xi的系数 - 确定符号
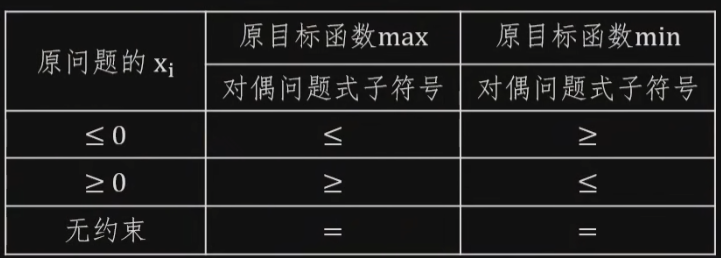
7.确定变量范围
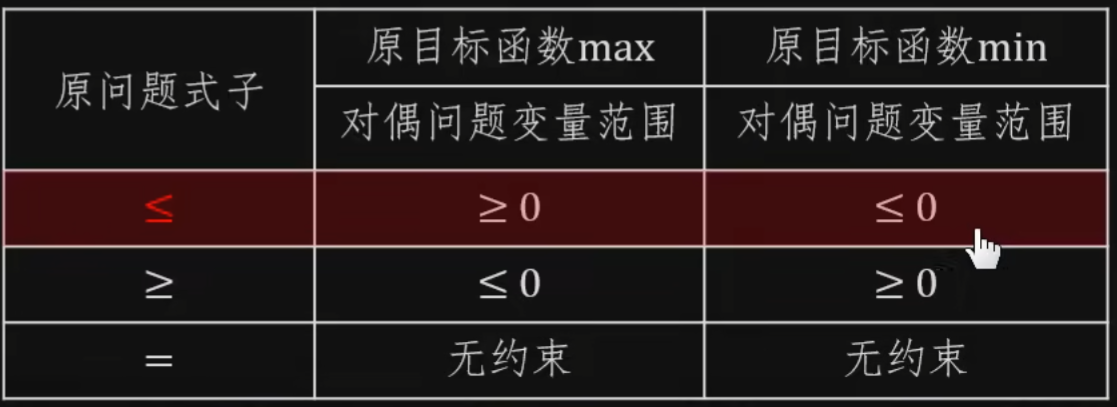
对偶问题求解

例题

标准单纯性表
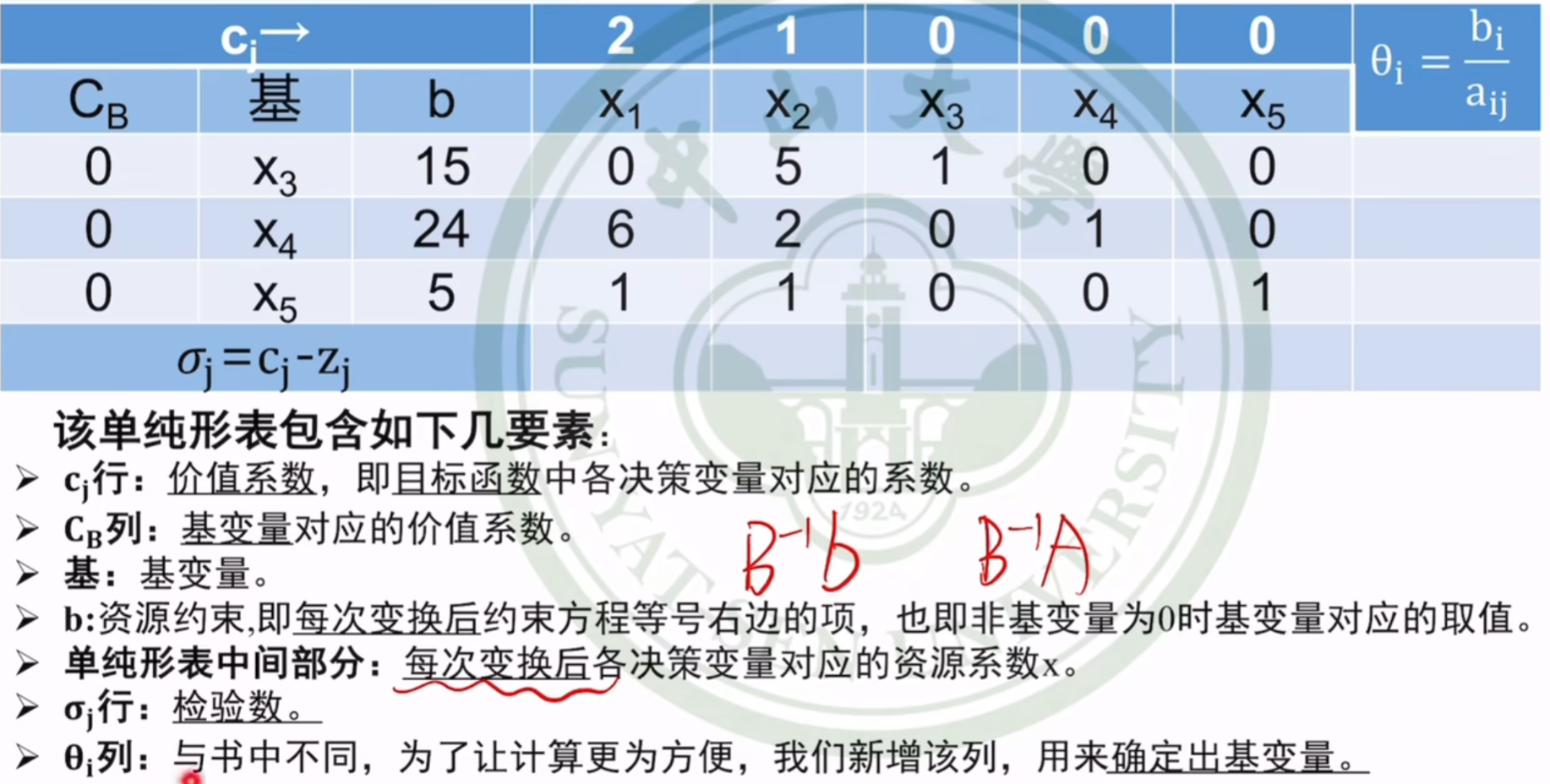
- b b b和 A A A【系数量】每次迭代都会变化
检验数的可能情况,选入基变量

- 基变量的检验数一定是0
- 如果存在大于0的检验数,取最大的作为入基变量
选出基变量并迭代
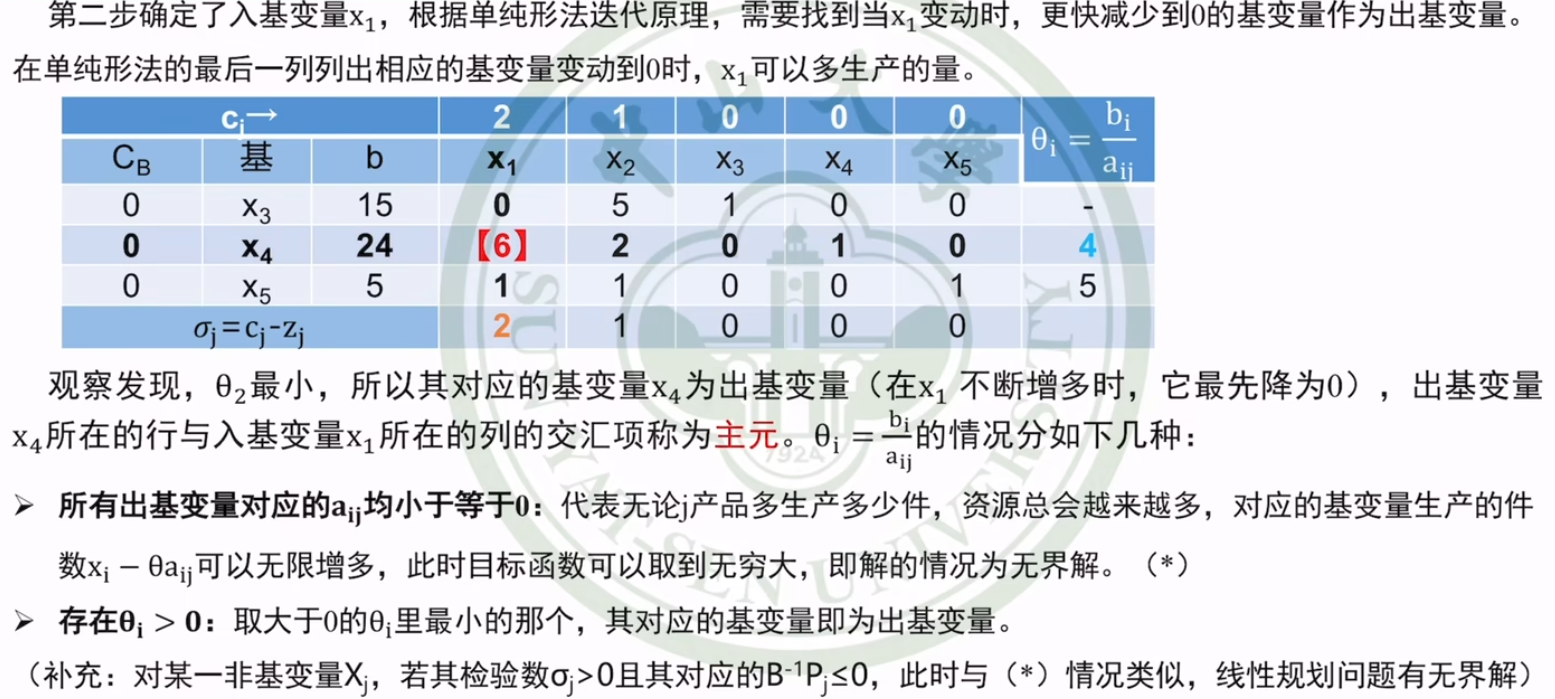
-
计算 θ \theta θ,负的和0不用管,选择最小的一项,该行对应基变量出基
-
若全部 a i j a_{ij} aij均小于等于零,相当于资源越来越多
迭代
用行变换,把入基变量那一列变标准
例题二【大M法,不考】

加人工变量
加入人工向量,并设置条件让它强制为0

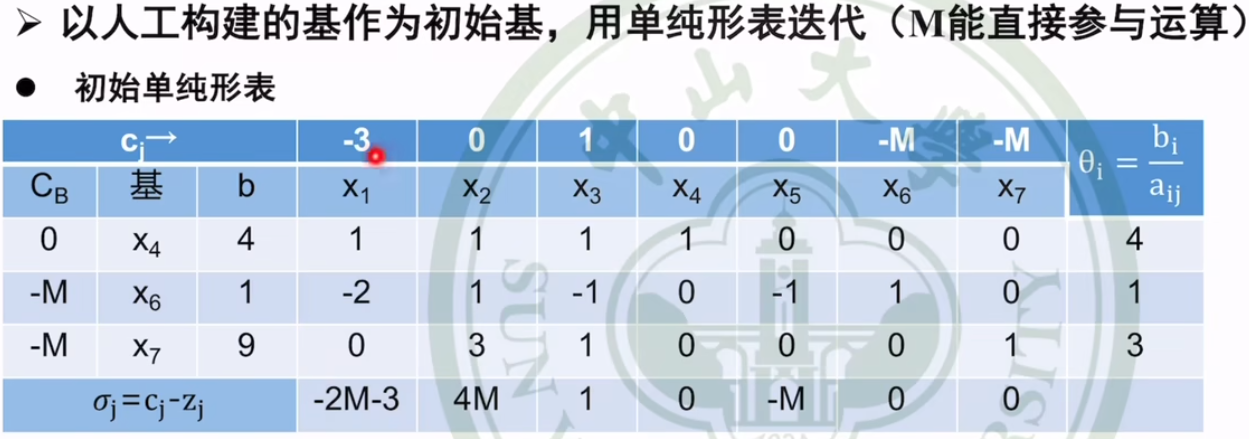
例题三【两阶段法,与大M法目的相似,解决的是基变量不足时的问题】

第一阶段:添加人工变量

迭代,直到人工变量被全部筛选出
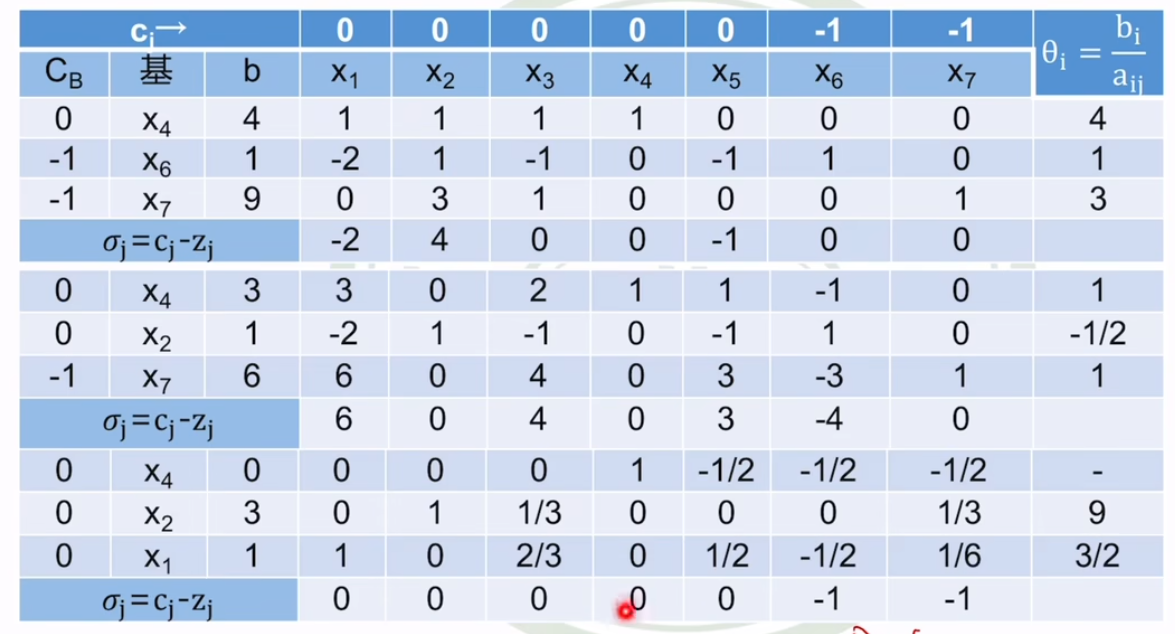
- 注意目标函数变了,
c
j
c_j
cj是人工变量取
-1
第二阶段:单纯形表
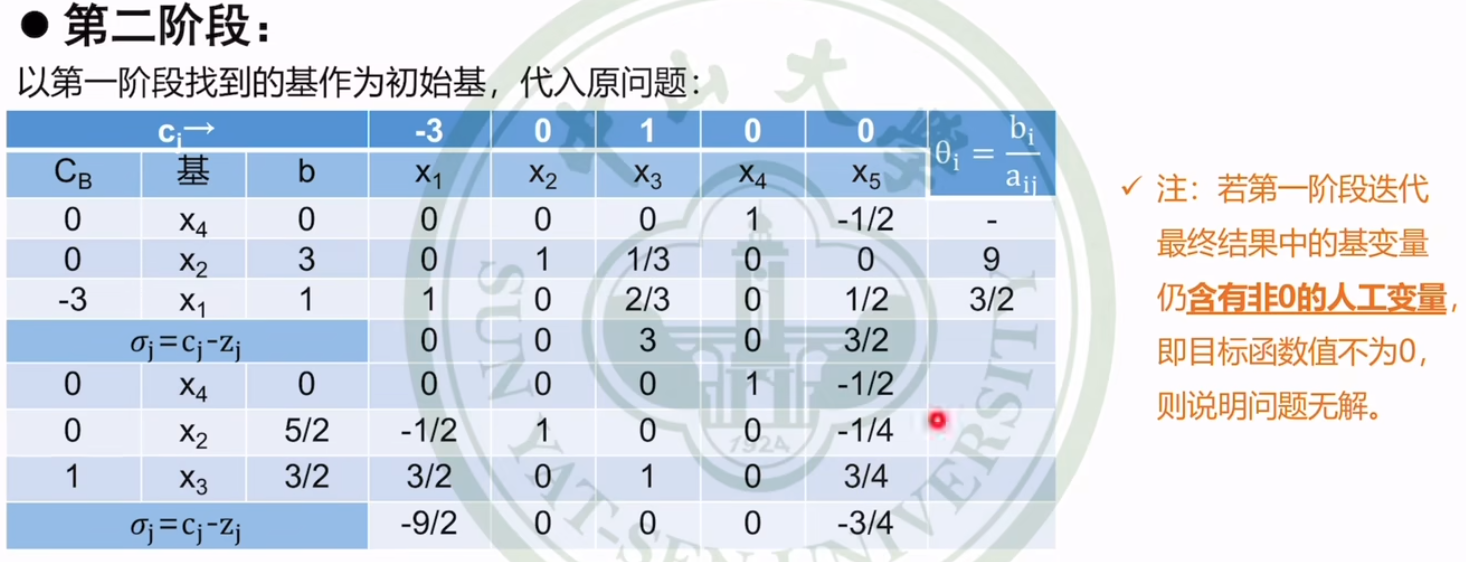
-
注意 c j c_j cj变成原来的了
-
人工变量法和两阶段法中,当求解结果出现所有检验数均小于等于0,但基变量中仍存在非零的人工变量(两阶段法第一阶段目标函数值不为0)时,表明问题无可行解.
即人工变量最终求解结果必须为0







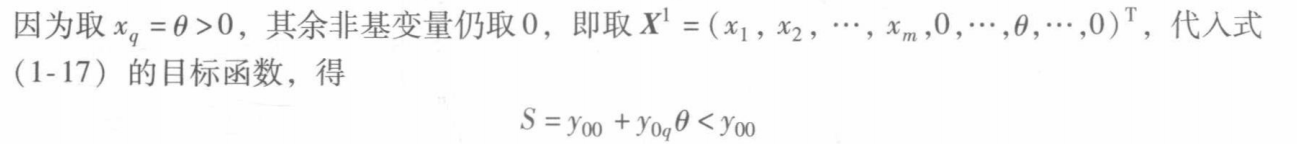













 1297
1297











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








