交通｜考虑乘客选择的航班调度策略解读

编者按：

乘客在选择机票时，行程的便捷性是一个至关重要的因素。然而，由于乘客偏好的数据的不足和其造成的计算的复杂性，现有的航班调度方法往往没有充分考虑到这一点。这篇推文将会介绍由同济大学助理教授的魏可佶和其两位导师达特茅斯赛尔工学院的Vikrant Vaze教授和麻省理工斯隆管理学院的Alexandre Jacquillat教授提出的新的航班调度和时刻表定制策略。他们的模型融合了乘客的选择，实验结果表明，这一创新策略不仅可以为乘客提供更为便捷的航班时刻表，同时也能为航空公司创造更高的利润，这一研究成果有望推动大数据驱动背景下航空业的发展。

引言

航班时刻表和机型的优化对于航空公司的运营利润影响重大，但由数据驱动或基于模型的定制方法仍然实际应用比较有限的。时刻表的优化问题非常复杂，这不仅因为它与航空公司的飞机调度决策存在强烈的相互依存性，同时也因为航班的出发和到达时间往往是乘客在选择买哪一趟行程时的重要决定因素。作者发现，在现有文献中，大多数方法都是依赖于增量式航班时刻表定制的方法，也就是在现有时刻表的基础上进行不断增改。而本文提出的优化模型则关注如何从零开始优化一个完整的航班时刻表，同时使用离散选择模型来描述乘客的选择行为，从而构建了一个集成的航班时刻表和飞机机型调度的优化模型。此外，本文还提出了一种高效的多阶段求解方法，可以在有限的计算资源内优化航空公司的时刻表和机型。最后，通过以阿拉斯加航空公司的数据作为案例研究，作者发现，与最先进的增量飞行时刻表定制方法相比，本文提出的模型公式与求解方法能够显著地提高航空公司的利润，同时也更好地满足乘客的出行需求。

一、模型介绍(航班时刻表制定与飞机调度模型)

1. 乘客购票选择的描述

相较于最常用的多项Logit模型（MNL）模型，作者使用了Gallego, Ratliff, and Shebalov于2015年提出的广义吸引模型（Generalized Attraction Model，GAM）来描述乘客购买航线产品的决策。相对于MNL模型，GAM模型的一个潜在优势在于它规避了MNL模型的IIA特性，即无关方案的独立性（Independent of Irrelevant Alternatives）。在MNL模型中，任意两个方案被选中的概率之比仅与这两个方案本身的属性有关，而与其他方案的特点无关。然而，在我们的问题背景下，这显然是不太现实的，因为不同的票价产品可能共享一些相似的属性，例如在相同的出发地和目的地下，不同的票价产品可能具有相近的行驶时间。

具体来讲，GAM是通过考虑产品不可用时潜在替代方案的影子吸引力（shadow attractiveness），来实现对乘客购买航线产品的决策更为准确的刻画。我们考虑由承运航空公司提供的所有行程的集合是 $I$，并假设实际可供选择的行程集合为 $I^{\prime }$， $I^{\prime }\subset I$。这里将$A_i$表示为行程 $i$的吸引力，$A_O$表示为外部选择的吸引力，也就是所有其他航空公司行程产品以及选择不乘飞机的吸引力值总和。在GAM中，通过用 $w_i$表示每个行程 $i\in I$的影子吸引力，乘客选择行程 $i\in I^{\prime }$的概率可以被表示为：

不难发现，当分母中间的那部分的影子吸引力为0时，这个模型也就是我们所熟知的MNL模型。

2. 优化模型的构造

在这篇推文里，我们着眼于解释优化模型的主要构造原理，特意省略了具体的数学模型表达，以便更容易理解。感兴趣的读者可以对照我们的解读，回到原文去看具体的表达式。

总的来说，作者采用了Hane等人于1995年提出的时空网络来对航班时刻表和调度决策进行建模，并定义这个网络里的每个节点代表着一个独特的机型、机场和时间段的组合，每个航班弧的起始节点对应着计划的起飞时间，而结束节点则对应着飞机降落后准备好下一次起飞的时间。

一些关于调度决策的假设和细节：

• 假设：模型专注于一天内的调度决策，将整个时间划分为时长15分钟的时间段。同时，为了防止在短时间内出现过多的航班拥堵，我们对于同一时间段内的直达航班进行了限制，确保不会安排两个机场之间的直达航班超过一次。此外，为了简化模型的设计，我们还假设航班时刻表以天为单位重复。
• 主要的决策变量：0-1变量 $x_{s,f,t}$，当把机型 $f$分配给航段 $s$上的某个航班且出发时间段为 $t$时等于1。
• 目标函数：最大化航空公司的总运营利润，该函数被定义为总的票价收入（跨所有市场、所有乘客类型和所有票价等级的所有行程）减去所有计划飞行的总成本（跨所有航段、所有机型和所有出发时间段）。
• 除变量的定义域约束之外，约束条件分可以为五类：
  • 飞机可用性约束：限制了分配给每种类型飞机的数量不能超过航空公司机队中可用的数量；
  • 流量平衡约束：简单点说，在时空网络模型，航班网络中飞机的流量守恒就是希望保证每种机型的飞机进入节点的数量等于离开的数量，除此之外，由于我们的模型是一个每日调度模型，我们希望每个机场停放的飞机数量在一天开始时和结束时必须相同；
  • 需求和容量约束：这类约束确保每个行程-票价级别组合产品的市场份额与其吸引力是成比例的，这个约束嵌入了一个线性化版本的乘客购票选择模型 （Sales based Linear Programming）；
  • 行程选择约束：如果任何行程的任一组成航段未运营，则不能将乘客分配给该行程；
  • 航段变量的限制约束：每个航段在每个时间段内最多运营一次，并且每个航段上的总航班数量应等于该航段的每日频率。注意，每日航班频率是模型的输入，原文中的第6节也进一步讨论了怎么将频率规划纳入建模框架中。
• 不难发现，最后构造出来的优化模型是一个混合整数线性规划（MILP）模型，接下来我们看看作者是怎么来求解的。

二、求解方法

在前文介绍的数学模型中，我们可以看到其规模对于与任何国际航空公司的网络对应的问题实例来说都是非常庞大的。由于时刻表被离散化为15分钟的时间段，6点到午夜之间的时间窗口包含18×4=72个时间段。在本文中最大的案例研究中，我们考虑了包含299个航段和7种机型的情景。回顾前文介绍的决策变量定义，每个变量都对应一个航段、机型和时间段的组合，因此总共有299×7×72 = 150696个0-1决策变量。这一庞大的规模使得直接使用商业求解器求解可能会非常困难，甚至可能根本解不出来。在本文中，作者提出了一种逐步缩小决策出发时间范围的方法来应对计算上的挑战，通过将整个计算过程划分为多个阶段，从而提高求解效率。

具体而言，第一阶段先以机场为单位合并多个连续的时间段，然后确定每个航班应该在哪一个合并的时间段出发。第二阶段使用第一阶段的解决方案作为输入，确定每个航班应该安排在哪个更窄的时间段内。第三阶段与第二阶段相似，但进一步缩小了时间段，以此类推。通过这种逐步缩小时间范围的方式，作者成功地将庞大的计算问题分解为更好求解的子问题，从而有效地提高了求解效率。

此外，作者还引入了两种启发式算法来加速这个多阶段求解MILP模型的过程，并且在后续的实验中证实了它们对计算性能上的显著提高作用。

• 固定机型：该方法的核心思想是在阶段I的最优解基础上固定每个航段的机型分配，以使得阶段II模型能够专注于时刻表决策，从而显著减少了阶段II中的决策变量数量。
• 航段对称：该方法的核心思想是要求任何机型在任何航段上执行的航班数量等于该机型在“对称航段”（将起点和终点互换的航段）上执行的航班数量，从而将0-1决策变量（即 $x_{s,f,t}$变量）的数量减半。

这些启发式算法可能存在生成次优解的风险，但本文的实验结果表明，计算上的优势是大过产生次优解的风险的。

三、实验结果

1. 计算结果对比

作者基于阿拉斯加航空公司的网络数据，将本文提出的计算方法、启发式算法及CPLEX在特定时间内，进行计算性能对比，然后分析了各自目标函数值随时间的演化情况。

（1）实验设置

作者设计了一系列航空网络增长的测试实例，并设定了5个网络，网络相关参数如表2所示。

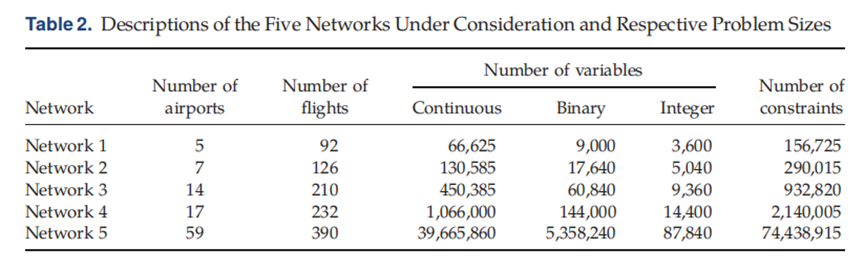
作者将机票价格作为模型的输入参数，同时，对模型计算的参数，做了如下设定：

1）只考虑直达和一站式的行程；2）飞机的最小周转时间均假定为45分钟；3）乘客转机时间设定在45到180分钟范围内；4）乘客类型和票价等级只考虑一种。

（2）启发式算法的对比

之后，作者将前文提到的七种启发式算法与多阶段求解方法进行了对比。另外，作者将直接运行CPLEX不同时长所得的解，设定为两个基准，一个是“CPLEX Short （2 hours）”，一个是“CPLEX Long (48 hours)”，将计算的解分别与CPLEX Long的解进行对比，计算结果如表3所示。

从表3可以看出，正的结果均表明了相应求解方法获得了比直接运行CPLEX更长时间产生了更大的营业利润，同时，也进一步表明了，与直接运行CPLEX相比，多阶段求解方法和启发式方法产生了更优的解，并且网络规模越大，改进越明显。

（3）目标函数值随运行时间的演化

接下来，作者利用网络5，以启发式方法4为求解方法，分别设定阶段I和阶段II不同的运行时间，并与直接运行CPLEX48小时，分别将它们以不同颜色绘制，观察其目标函数值演化如图2。

图中，x轴对应于整个启发式方法的总运行时间（阶段I+阶段II），y轴对应最优解对应的目标函数值。

图2显示了两条水平线和四条曲线。其中，黑色直线表示通过直接运行CPLEX 48小时后获得的目标函数值；绿色直线表示启发式方法4通过在阶段I持续运行24小时，然后运行阶段II，直到内存耗尽（即1.5小时）后的目标函数值；剩余4条曲线，则分别对应阶段I不同的运行时间（即半小时、1小时、2小时和4小时）的目标函数值变化。

从图中可以看出，运行求解器两个多小时后初始解被找到，即使再运行15个小时，目标函数值进一步的改善便十分微小。对于启发式算法而言，结果相反，随着将它们的运行时间增加到两个小时以上，解的质量便有了更快更早地提高。然而这种关系是非线性的。例如，曲线对应于一小时和两小时的阶段I运行时间，具有相同的最终目标函数值，这意味着在阶段I中花费的额外小时无助于找到更好的最终解。相比之下，将阶段I的运行时间从两小时增加到四小时后，对于最终的利润值便会产生一个显著的改善。此图可以为航司在有限时间内z最大化利润提供参考。

2. 时刻表的益处

（1）实验设置

作者固定了所有飞行时刻表和飞机调度决策变量的真实值，并复制了乘客对这些特定航班的预定决策，并将其命名为Baseline 0。又以仅优化飞机调度决策、优化飞机调度决策和飞机时间增量变化以及允许消除指定的可选航班子集，分别定义了Baseline 1、Baseline 2-a、Baseline 2-b、Baseline 3-a、Baseline 3-b。

（2）模型及计算架构的益处

作者以阿拉斯加航空公司网络5为例，将Cplex Directly 及启发式方法5、6，与每个基线方法的计算情况进行对比分析。

表4可以看出，若以各种方法利润的表现进行排序，基线0<基线1<基线2-a<基线3-a<基线2-b<基线3-b= CPLEX Directly <启发式6<启发式5。结果表明，相比现有方法，本文提出的整合时刻表和飞机调度的模型，同时结合文中的启发式求解方法可以提供极大的利润改善。

3. 拓展

（1）多种乘客和票价类型的影响

作者前文的结果，均是基于单一的乘客类型和票价类别做出的计算，不同行程属性的乘客是不同的。一般而言，商务旅行者通常更重视日程安排的便利性和灵活性，以休闲为目的的乘客往往对价格更为敏感。航空公司在设定航班起飞时间之前，通过不同的营销手段，针对不同的乘客可以提供各种票价等级。

本节中，作者引入三个参数K1、K2、K3，模拟了各种假设的市场细分和定价情景。作者假设乘客类型只有两类，即商务和休闲。K1表征两个票价类别之间的票价差异，K2代表每个市场中商务乘客的比例，K3则是区分商务和休闲乘客的效用函数。

从表6可以看出，与向所有乘客收取单一票价相比，提供两个不同的票价，可以实现总利润的显著增加，增加的收入来自于商务乘客购买更高票价的机票，并且随着商务乘客比例越高，利润的改善则越显著。这再次强调了，市场细分与差异定价对航空公司运营的影响。

（2）融合频率计划的决策

相比仅优化时刻表和飞机调度决策，结合优化的飞行频率、时刻表，以及飞机调度决策，可能带来更大的收益利润增加。然而，飞行频率的决定也取决于各种战略和运营考虑因素，鉴于问题的复杂性，作者分析了增量频率规划灵活性的影响，允许每日频率在每个分段现有频率值的±1和±2范围内波动。

由表可以得出，由于航班数量的大部分增长都在枢纽-轴辐和轴辐-轴辐部分，一站式收入实现了大幅增长。这些额外的航班，对直达航班收入增加的影响是有限的，但通过向许多无法支持直达航班的低需求市场提供更好的转机服务，却使得一站式收入实现了大幅的增长。

（3）航空公司合并的影响

作者以阿拉斯加航空公司与维珍美国航空公司合并为例，分析了航空公司合并对时间表优化产生的影响。

表8中，以第4列数据为基准，对直达式和一站式的乘客及利润增减变化情况进行了分析。结果表明，仅仅合并本身带来的好处相对较小，但通过对航班时刻表和飞机重新分配，却可以带来了利润的显著改善。此外，作者还发现，在合并后的每一种情况下，乘客总数虽然都低于合并前，但产生的利润却高于合并前，这表明了更多的乘客并不一定会带来更多的利润。

之后作者对合并前后，各个机场利润的变化情况进行分析。可以看出，除原来阿拉斯加航空公司的SEA、PDX、ANC收入下降外，其余机场收入均实现了增长。这再次印证了本文所提方法的优越性，即融合了乘客选择的飞机时刻表和飞机调度策略能够充分利用两家航空公司合并后的网络，实现对资源的重新配置，由此产生更多的乘客转机机会，进一步提高航空公司的盈利能力。

四、小结

本文的作者提出了一个基于内生性乘客的选择，建模和计算架构同时综合了时刻表和飞机调度，给定每个直达航班的飞行频率，乘客需求无约束，该方法产生的航班时刻表和飞机调度解，最大限度地提高了航空公司的利润。由于问题规模的复杂性，作者还特别设计了一个多阶段计算框架，以及启发式方法，以实现模型在合理时间内计算求解。

然后作者利用美国已有的航空公司的数据作为案例分析，计算结果表明，本文的算法要显著优于直接使用商业混合整数优化求解器得到的结果。区别于现有文献及计算方法，作者将模型与求解方法进行了整合，这进一步引发了利润的显著改善。最后，作者又从三个方面对本文的问题进行了扩展，分别是市场细分和差异定价、融合频率规划决策以及航空公司合并，这些实验和结果都进一步证明了作者方法的多功能性和可用性。

这段文字提到的魏可佶目前是同济大学经管学院的助理教授，专长领域包括航空运营管理。如果你对他的研究或者相关领域有兴趣，可以通过提供的电子邮箱keji.wei@tongji.edu.cn与他联系。

参考文献

[1] Wei, Keji, Vikrant Vaze, and Alexandre Jacquillat. “Airline timetable development and fleet assignment incorporating passenger choice.” Transportation Science 54.1 (2020): 139-163.

[2] https://mitsloan.mit.edu/press/mit-sloan-and-dartmouth-research-develops-airline-scheduling-tool-to-optimize-flights-and-increase-profits