1.Planar Homographies
单应矩阵
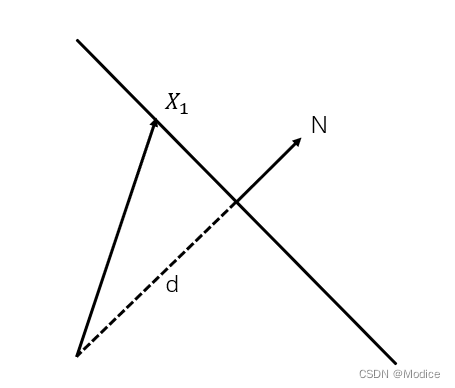
假定场景的点都落在一个平面上,第一帧定义点坐标系,平面的法向量
,有
第二帧有如下关系
其中
H是单应矩阵,引入2D坐标系有
这个表达式是平面单应矩阵,从上式可以看出H与相机的旋转、平移以及平面的参数有关。
与对极几何相似的处理,左右同乘
称为平面对极约束或平面单应约束。
同样也可以写成下述形式,
2.The Four Point Algorithm
四点算法
假定有两幅图中四对以上的2D相关点,每个点对引入一个矩阵
,形成一个大矩阵
可以看出四点法与八点法类似,四点算法中H分解为R,N和T/d。
本质矩阵与单应矩阵
存在很多的关系,如






















 6447
6447











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








