Planar Homographies (平面单应矩阵)

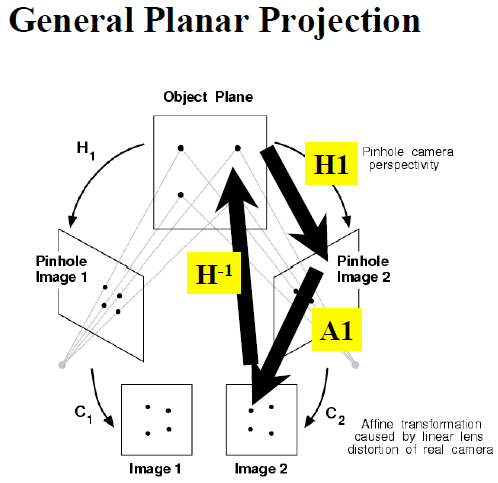
1. 平面投影

1.1 平面单应矩阵

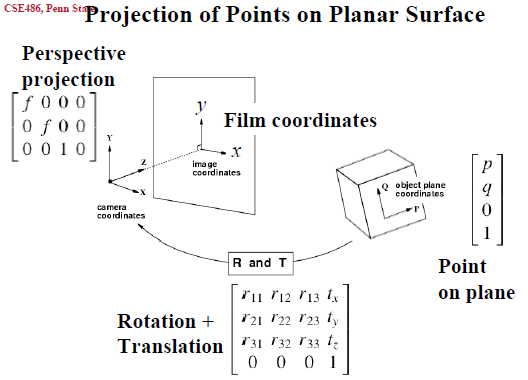
    平面单应矩阵：就是平面的投影变换矩阵。

    Homography matrix (单应性矩阵)：
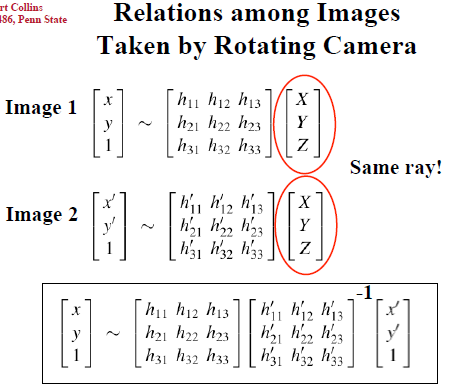
        两个不同视角的图像上的点对的homogeneous coordinate可以用一个投影变换（projective transformation）表述，即：
        x1 =H*x2
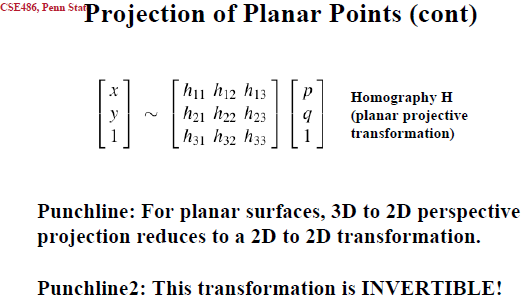
       投影变换也叫“单应”--Homography，因此H就叫单应性矩阵。上式中的x1和x2都是3*1的齐次坐标，因此H是一个3*3的矩阵：{h00,h01,h02;h10,h11,h12;h20,h21,h22}。

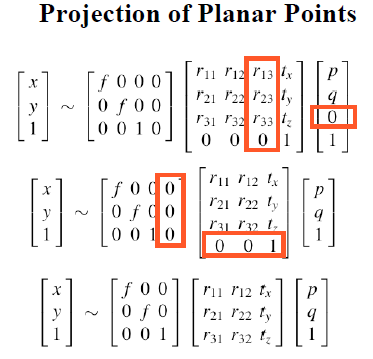
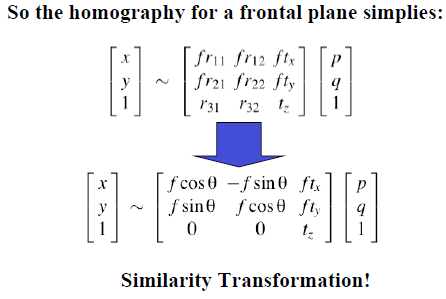
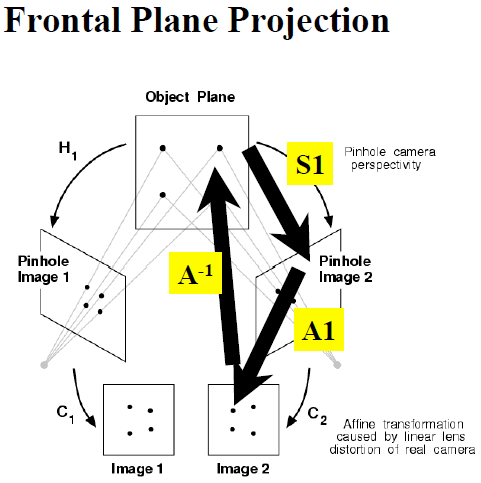
1.2 正面图投影（Frontal Plane）

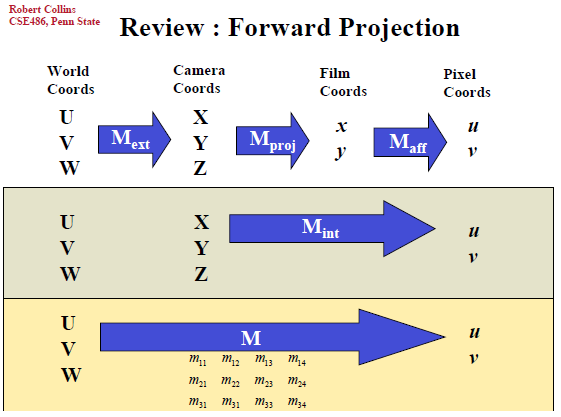
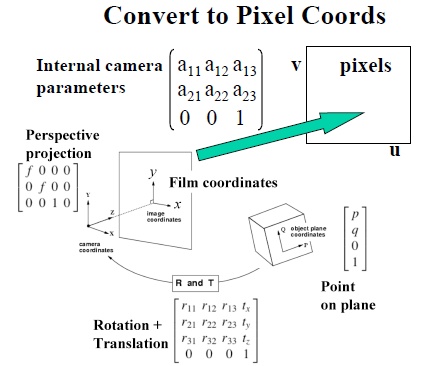
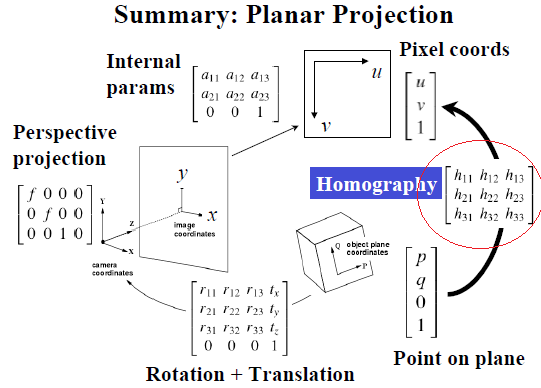
1.3 转换为像素坐标

1.4 总结

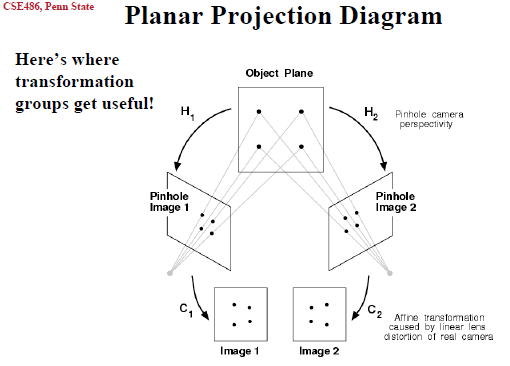
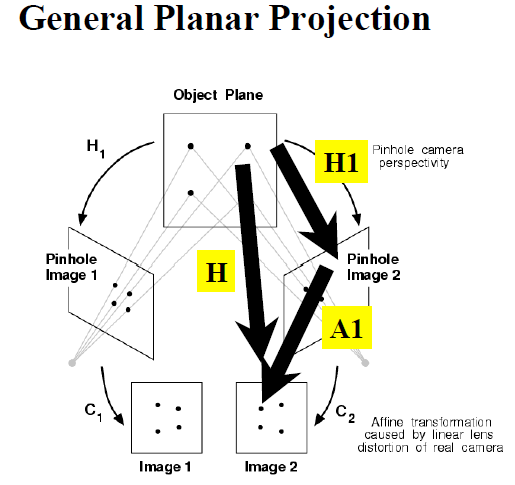
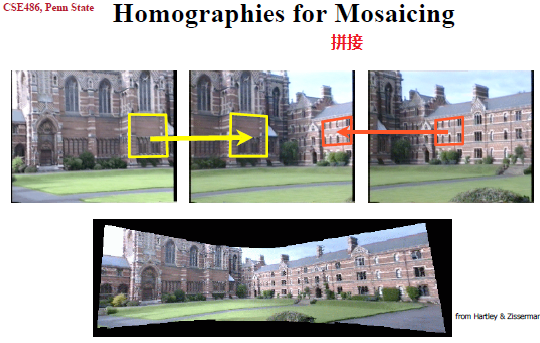
2. 单应矩阵的用途

3. 如何估计单应矩阵

代数、几何、分析 各自的范畴：
    数学中研究数的部分属于代数学的范畴；研究形的部分，属于几何学的范筹；沟通形与数且涉及极限运算的部分，属于分析学的范围。这三大类数学构成了整个数学的本体与核心。在这一核心的周围，由于数学通过数与形这两个概念，与其它科学互相渗透，而出现了许多边缘学科和交叉学科。

Algebraic Distance: 代数距离

    

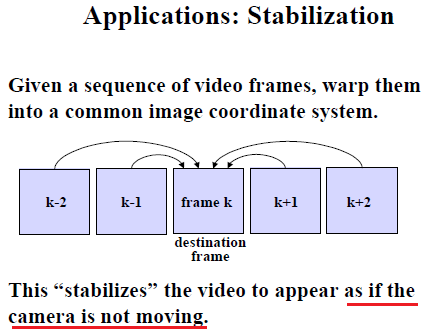
4. 应用：稳定性

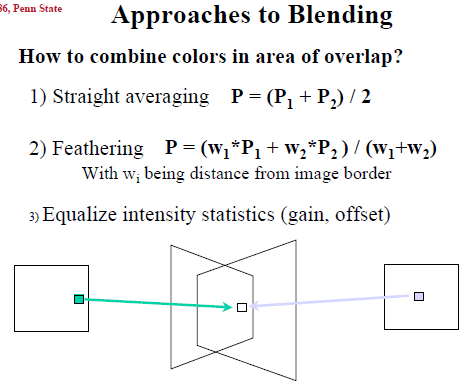
5. 应用：360度全景图