2.模拟电子技术学习笔记

写在前面

这是这个系列的第二期，我预计会在26号我自己开学前更新完这个系列。上一期我们通过最基础的参杂半导体引出pn节的概念，这节课我们深入的讲解pn节以及相关性质。这一期如果是使用博伊尔斯塔德那本书的就是二极管的部分内容，他那本书跟大多数人学的（至少是我学的）有一点差别在于，由于二极管就是一个pn节进行封装，博伊尔斯塔德那本书以二极管这个最简单的半导体元器件为入手点讲解的相关的概念，但总体的知识点都是大差不差的。好我们开始这一期的学习内容

pn节的相关性质

我们现在有了一个pn节，即两种参杂半导体拼在一起，我们不加电压，上一期我们讲过，在中间就会形成一个耗尽层，也就是pn节。但是这个“耗尽层”难道就没有载流子经过吗？显然不一定，总会有各自的多子由于热运动，有那么一两个“厉害的”会过去。这个过程可以这么描述：

(在耗尽层中)n型材料的多数载流子必须克服正离子层的引力以及p性材料中负离子层的的阻碍才能移动至p型材料耗尽层以外的区域与此同时，p型半导体的空穴也有类似的事情发生。

在耗尽层中的少子（以n型半导体的空穴为例），我们可以看到，耗尽层的电场方向正好是n指向p，这会“帮助”少子移动到另一个半导体上，我们称这种现象为漂移运动。

这时候有好事者会加上一个电压，我们看着这个原始的不加电压的图来考虑考虑如果我们加上电压会发生什么

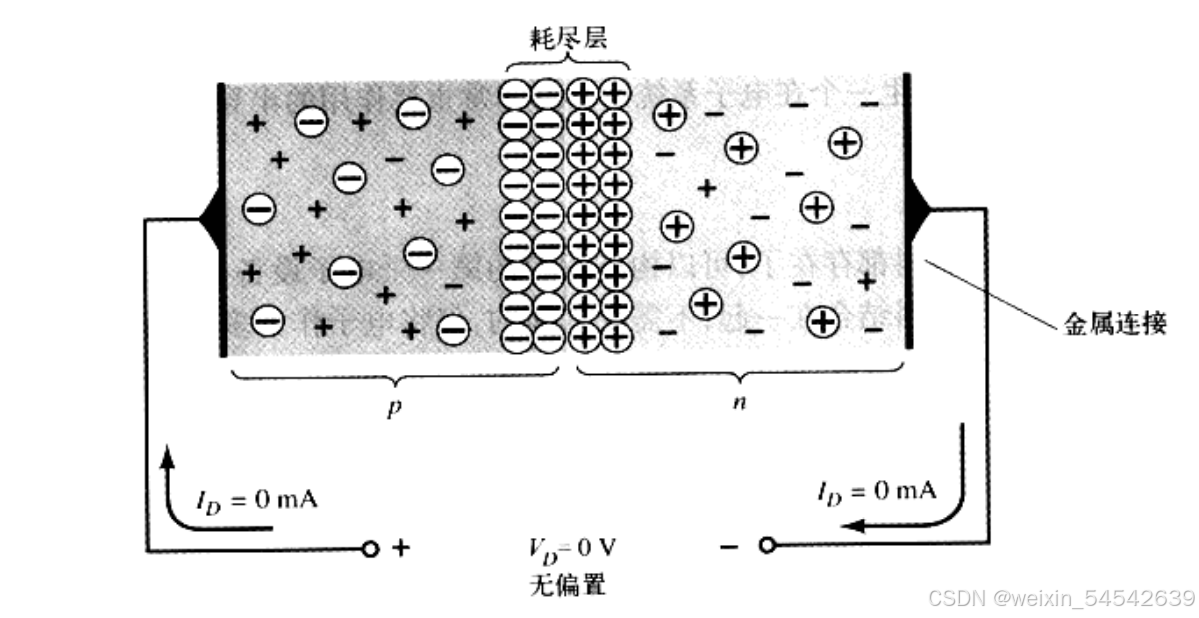
这个耗尽层的电场方向显然是从右到左的，那么如果我们加上与之相同的电压会发生什么呢？是不是说，以右侧的自由电子为例，会将这些自由电子推到更右面，同理会将左面的空穴推到更左边。这样，我们这个所谓的“停战区”，即耗尽层的范围就会变得更大：

那么这时多子向另一个半导体的运动就会变得更加困难（因为耗尽层的电荷变多了，耗尽层对多子运动的阻碍就变大了），但是少数载流子的漂移运动的数量是不变的，这种由少子的漂移运动形成的电流我们叫它反向饱和电流，用Is表示。它很小，几乎可以忽略不计。

欸，这时就会有同学问，这不是沿着耗尽层的电场方向加的电压吗，怎么就是“反向”了？这个问题就引出来了我们的下一个问题：如果我们逆着这个耗尽层的电场方向加电压会发生些很么呢

显然，如果反向加一个电压，我们想象一下，两边的半导体各自的多子是不是说会向中间靠拢（自己画一下电场方向就清楚了）这时候两边多子的结合的概率就会变大（因为都到中间来了吗）我们这时候还是像上一期那样把这个多子和少子的结合想象成一场战争，这个耗尽层就是“停战区”如果两边的结合越来越多，是不是就是这个“战争”非常激烈，这个“停战区”是不是会变得的非常小，也就是耗尽层变薄（因为都想“打仗”，这个“都想”就是我们这个电场把两边的多子往中间凑的结果）

如果反应过来的同学也可以这么理解：反着这个耗尽层的电场方向加的电场削弱了原来的耗尽层对各自多子的阻碍作用，从而也可以推出这个耗尽层变薄的结果

耗尽层的阻碍作用减少，会导致多数载流子的运动，进而会导致这个材质里面会产生电流，我们看这个空穴，为什么看空穴呢，因为空穴是正电荷，电流方向不是正电荷的移动方向吗，那么我们会发现，这个空穴的自发的扩散运动是自p向n的，与电流方向相同（看上面那张图），而我们逆着耗尽层电场方向会更有利于这个扩散运动的进行。这时这个材料的性质和导体相差无几，这个方向的电压我们规定为正向电压，有些书也管他叫正向偏置（Forward-Bias Condition）,而我们刚才说的顺着耗尽层加电压的方向就叫做反向偏置（Reverse-Bias Condition）。正向偏置由于是多子的运动，他的电流大小与纯导体在很大程度上相差无几，为什么说是相差无几呢，我们待会说。

那么我们就会得到这样一个神奇的材料：如果电压正向偏置，它的电流就会很大，接近于导体，如果电压反向偏置，他会得到一个固定的反向饱和电流，这个电流很小，小到几乎可以忽略不计，接近于断路。这样的性质是我们以前所接触的电阻，电容，电感中从来没接触过的性质，只在一个方向导通，另一个方向几乎是断路。这种性质我们叫做pn节的单向导电性。这种材料的出现意味着我们可以规定电流的路径，只许这么流，不允许反过来。后人利用这个性质做出了人类历史上第一个半导体元器件，答案想必呼之欲出，那就是——半导体二极管！

势垒电容和扩散电容

就在刚才，我们成功的发明了二极管，但是我们平复一下兴奋的心情，来思考一个东西。

我们就看这张图：

我们想，这个是不是有点像一个电容，诶先别急，大家想哈，电容是什么，很多同学都知道，C=Q/U吗，这有啥不知道的，是不是从另一个角度说，如果我们想象一个传统的电容，电容值是固定的，是不是很容易就的出来，随着电压值的变化，电荷值也随之变化，电荷随着电压的变化而变化，我们就可以把它叫做电容。那么我们来看这个，现在我们虽然没有具体的电压与耗尽层电荷量的关系，但是我们可以想一件事，就是如果我们的电压反向偏置，耗尽层的电荷量显然是多的，如果电压正向偏置，那么耗尽层的电荷量是很少的，那么我们虽然不知道具体的关系，但是我们可以知道耗尽层的电荷量与电压是有关系的，电荷随着电压的变化而变化。我们管他叫做势垒电容。

诶，这时会有同学问了，为什么叫势垒这个词？这与我在前面讲解的正向偏置和反向偏置有关。我们以正向偏置为例，对右侧耗尽层的自由电子来说，左侧耗尽层的负电荷对它向左扩散来说就是个“阻碍”，左侧电势低，电势能高，对于想要向左去的自由电子来说就是一个巨大的“势垒”，对于左侧的空穴也是如此，同学们自己画一下电场就明白了。对于两侧的多子，显然对侧的耗尽层形成了一个势垒，所以由耗尽层形成的电容我们称之为“势垒电容”。

接下来我们再看，各自的多子都在向对面扩散，根据我们前面的分析，我们可以知道，如果电压正向偏置，向对侧扩散的多子的电荷数就会变多，反之，如果电压反向偏置，那么向对侧扩散的多子的电荷数就会变少，电荷随着电压的变化而变化，我们管它叫做扩散电容（由于多子的扩散作用形成的电容）

半导体二极管的伏安特性曲线

看到这个曲线很多同学会有两个疑问：第一个是反向饱和电流去哪了？由于反向饱和电流很小，这张图并没有显现出来，第二个问题就是，后面反向电压到一定程度之后怎么就无限大了？这个问题值得研究，我们后面会详细讲到。

这个曲线有一公式，叫肖克利方程（Shockley's Equation）：

VD就是我们这个伏安特性曲线的自变量，n我们一般取1，Is就是反向饱和电流。VT（我学的时候叫UT）是一个温度当量，与伯利兹曼常数k，温度T，元电荷e（1.6E-19C）（博伊尔斯塔德那本书叫q）相关。有些书可能给出了公式：

对于这个伏安特性曲线，我们从正向偏置到反向偏置开始一块一块的说

最右面的就是导通状态，这个就是符合我们刚才说过的肖克利公式。

再向左一点我们会看到有一块电流为0的地方，我们管它叫做死区（No-Bias）。死区的形成根据前面的分析也可以很好理解，正向导通就是相当于削弱了耗尽层对于两侧的半导体的多子的阻碍作用当电压比较小的时候，就相当于只削弱了一点，还不足以让多子过去，过了这个死区的电压之后，会有越来越多的多子跨过这个势垒，这个“越来越多”的过程就是这个肖克利公式。

再往左我们就到了电压反向偏置这部分。在一定的范围内有一个恒定的电流，我们称之为反向饱和电流，如果刚才这个图不够明显的话我们可以看这个图：

在整个图的最左侧我们会看到这个电流突然变大，这种现象我们管它叫反向击穿，这个区域我们叫做齐纳区域（Zener Region）。

今天就讲到这，我们下一期从击穿这部分开始讲起。

Checklist

今天涉及到的概念比较多，我列在这，供大家查缺补漏。

反向饱和电流，正向偏置，反向偏置，pn节的单向导电性，势垒电容和扩散电容，肖克利方程，温度当量，反向击穿，齐纳区域。

还有这个二极管的单向导通的推理过程建议自己再过一遍。

祝大家学习愉快！