D-FINE：将回归任务重新定义为细粒度分布细化。大白话带你掌握这篇论文主要的创新点，看完不用担心理解不了

在当前内卷严重的实时目标检测 (Real-time Object Detection) 领域，性能与效率始终是难以平衡的核心问题。绝大多数现有的 SOTA 方法仅依赖于更先进的模块替换或训练策略，导致性能逐渐趋于饱和。

为了打破这一瓶颈，来自中科大的研究团队提出了 D-FINE，重新定义了边界框回归任务。不同于传统的固定坐标预测，D-FINE 创新了两种方法：细粒度分布优化 (FDR) 和全局最优定位自蒸馏 (GO-LSD)。通过将回归任务转化为细粒度的分布优化任务，D-FINE 不仅显著简化了优化难度，还能够更精确地建模每条边界的不确定性。此外，D-FINE 将定位知识 (Localization Knowledge) 融入到模型输出，通过高效的自蒸馏策略在各层共享这些知识，因而在不增加额外训练成本的前提下，实现了性能的进一步显著提升。凭借这些创新，D-FINE 在 COCO 数据集上以 78 FPS 的速度取得了 59.3% 的平均精度 (AP)，远超 YOLOv10、YOLO11、RT-DETR v1/v2/v3 及 LW-DETR 等竞争对手，成为实时目标检测领域新的领跑者。

下面我们就具体讲解一下这两个创新点，包你掌握的。

一、细粒度分布优化 (FDR)

在理解这个创新点之前，我们需要知道一个你可能忘记的小知识点。

1.bbox分布与定位模糊性

bbox的表示通常是4个数值（也就是我们在一张图片中要检测物体，需要框把物体框起来，如上图检测人就把人框起来），一种方式就是我们需要在物体的左上，右下，来构建一个框。一种如FCOS中的点到上下左右四条边的距离(tblr)（确定一个中心点，这个中心点到上（t）下(b)左(l)右(r)的距离）,如上图的大象，它站在草堆里，我们在对它进行精准定位时，下边框是很难精确的，假设上图中，粉色是它的真实框（GT），目标检测中的边界盒回归传统上依赖于建模Dirac delta分布，然而，Dirac delta假设将边界盒边缘视为精确和固定的，也就是我们的预测框一定是和真实框重合才算预测正确，如上图大象下边框，黑色是很接近粉色真实框的，蓝色是距离比较远的，但是传统的回归就他俩都显示预测错误，在实际中，这种做法是不利于模型学习的，我们当然希望预测框越接近真实框越好，所以我们将这个问题用概率来解决，假设靠近真实框（粉色框）的黑色线的概率为0.9，蓝色线为0.4。那么用n个概率值去描述一条边，可以显示出模型对一个位置的定位模糊估计，我们利用这种概率来利于后续模型的学习。

所以Offset-bin则是针对encoded xywh形式建模出了bbox分布，它们共同之处就在于尝试将bbox回归看成一个分类问题。并且这带来的好处是可以建模出bbox的定位模糊性。

本论文解决的问题：虽然通过概率分布处理模糊性和不确定性方面向前迈进了一步，但其回归方法中的具体挑战仍然存在:(1)锚依赖:回归与锚盒中心绑定，限制了预测的多样性和与无锚框架的兼容性。(2)没有迭代细化:预测是一次性完成的，没有迭代细化，降低了回归的鲁棒性。(3)粗定位:固定的距离范围和均匀的仓间隔会导致粗定位，特别是对于小物体，因为每个仓代表的可能值范围很广。

解决方式：FDR 细粒度分布细化
初始框预测:与传统 DETR方法类似，D-FINE的解码器(decoder)会在第一层将 object queries 转变为若干个初始的边界框，这些框不需要特别精准，仅作为一种初始化。

细粒度的分布优化:D-FINE解码层不会像传统方法那样直接解码出新的边界框，而是基于这些初始化的边界框，生成四组概率分布;并迭代地对这四组概率分布进行逐层优化。这些分布本质上是作为检测框的一种“细粒度中间表征”;配合精心设计的加权函数 W(n),D-EINE 能够通过微调这些表征来实现对初始边界框的调整，包含对其上下左右边缘进行细微的小幅度修正亦或是大幅度的搬移。

对上面的初始框预测，细粒度的分布优化，进行详细解释，方便理解！！！

FDR通过迭代优化解码器层生成的细粒度分布（如下图所示）。

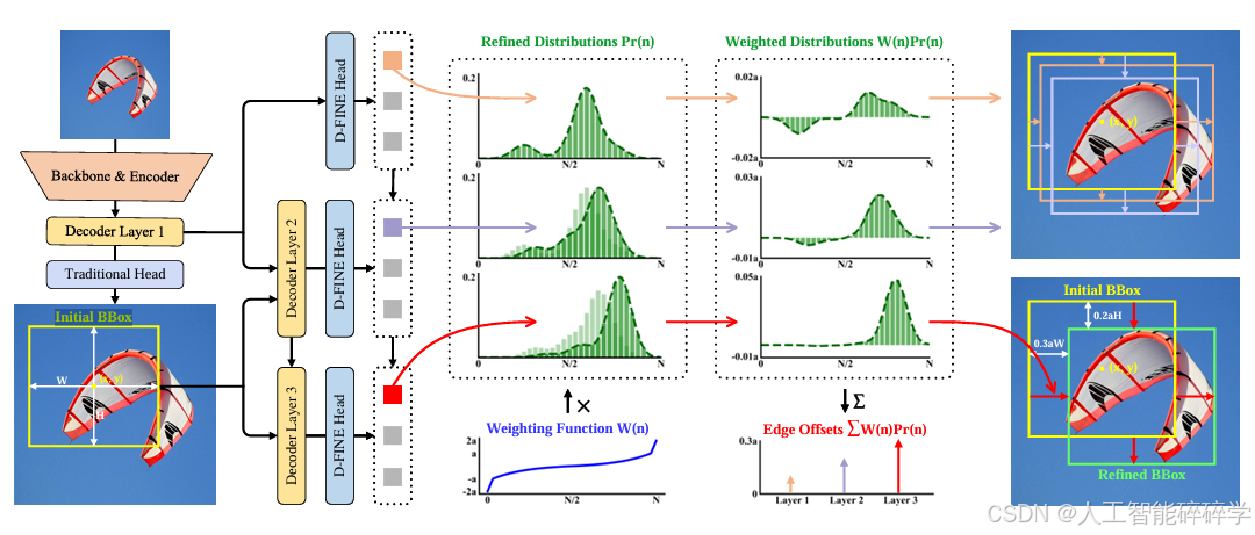
初始阶段，第一个解码层通过传统边界框回归头和D-FINE头​（均为MLP结构，仅输出维度不同）预测初步边界框和概率分布。每个边界框关联四条边的四个独立分布。初始边界框作为参考框，后续层通过残差方式逐步调整这些分布，从而优化边界框精度。具体流程如下：

• 设初始边界框预测为 b0​={x,y,W,H}，其中 {x,y} 表示边界框中心坐标，W 和 H 分别为宽度和高度。
• 将 b0​ 转换为中心坐标 c0​={x,y} 和边缘距离 d0​={t,b,l,r}，分别表示中心到上、下、左、右边界的距离。
• 对第 l 层，精修后的边缘距离 dl​={tl​,bl​,ll​,rl​} 计算公式为：
• 
  • Prl​(n)={Prt​(n),Prb​(n),Prl​(n),Prr​(n)} 表示四条边各自的候选偏移量概率分布（n 为离散的 bin 索引）。
  • W(n) 是权重函数，用于对每个 bin 的候选偏移量进行加权。
  • 最终的边距调整量通过 H 和 W 缩放，保证修正比例与初始边界框大小一致。

  • 精修后的分布通过残差调整进行更新，具体定义为：

  • 

     

    其中：

  • \logitsl−1​(n) 表示前一层的 ​bin 偏移量置信度​（即各 bin 对应边距调整的预测概率的对数）。
  • Δ\logitsl​(n) 为当前层预测的 ​残差对数，通过与前一层对数相加得到更新后的对数 \logitsl​(n)。
  • 最终通过 Softmax 归一化生成精修后的概率分布 Prl​(n)。

  • 权重函数 W(n)

    为实现灵活且精准的调整，权重函数 W(n) 定义为分段函数：

    

    其中 a 和 c 为超参数，控制权重的 ​上界​ 和 ​曲率。其作用如下：

  • ​预测接近准确时：
    • 权重曲线 W(n) 的曲率较小（中间区域平缓），允许对边距进行 ​精细微调。
  • ​预测较不准确时：
    • 权重曲线在边界附近曲率较大且变化剧烈（两端陡峭上升/下降），为大幅修正提供灵活性。

  • ---

    ​技术特点​

  • ​残差学习：通过叠加当前层与前一层的预测（Δ\logitsl​(n)+\logitsl−1​(n)），逐步优化边界框的分布。
  • ​动态权重分配：权重函数 W(n) 根据预测精度自适应调整，平衡精细调整与大范围修正的需求。
  • ​可扩展性：离散的 bin 索引 n 允许模型以离散化方式建模连续的边距调整空间。

精细化定位损失函数（FGL Loss）

为进一步提升分布预测的准确性并将其与真实值对齐，受分布焦点损失（DFL）​​（Li等人，2020）启发，我们提出一种新的损失函数——细粒度定位损失（FGL）​，其形式为：

损失函数这块就不细讲了。我们讲下一个创新点。

二、全局最优定位自蒸馏

在了解第二个创新点之前，我们先了解一点前景知识。

知识蒸馏

Knowledge Distillation*(KD)最早是针对图像分类而设计的。核心思想是:用一个预训练的大模型去指导一个小模型的学习，在保持模型性能的同时，减少模型的计算量和存储需求，使得学生模型能够在资源有限的环境中高效运行。

蒸馏过程：在训练学生模型时，不仅使用传统的硬标签（真实标签）来计算损失，还使用教师模型的输出（软标签）来计算损失。这样，学生模型通过最小化与教师模型输出的差异，从而学习到教师模型的知识。 损失函数通常包括两部分： 交叉熵损失（针对硬标签） KL散度损失（用于度量学生模型和教师模型输出概率分布之间的差异）。重点看一下KL散度损失。
KL散度损失：在训练学生模型时，我们希望学生模型的输出概率分布尽可能接近教师模型的输出概率分布。通过计算教师模型和学生模型之间的 KLD 损失，学生模型不仅学习到正确的类别（通过硬标签），还学习到教师模型在其他类别上的预测概率，从而获得更多的“知识”。

通过KLD损失传递定位知识：

定位知识（Localization Knowledge）：教师模型输出的概率分布携带了更多的信息，不仅是每个类别的预测概率，还包含了类别之间的相对关系（比如，猫和狗是相似的）。这些信息能够帮助学生模型更好地理解任务，尤其是在类别之间存在一定相似性的情况下。 通过计算 KLD 损失，学生模型在训练过程中能够从教师模型的概率分布中“蒸馏”出这种额外的知识，从而提高性能。 

全局最优定位自蒸馏
将知识蒸馏无痛应用到 FDR 框架检测器。搭载 FDR 框架的目标检测器满足了以下两点:

1.能够实现知识传递:概率即“知识”;网络输出变成了概率分布，而概率分布携带定位知识，而通过计算 KLD 损失，可以将这些“知识”从深层传递到浅层。这是传统固定框表示(狄拉克ō函数)无法实现的。

对第1点的解释：

1. 传统的固定框表示与狄拉克δ函数：

   • 狄拉克δ函数：在传统的分类任务中，我们使用 硬标签 作为目标。这些标签通常是离散的、固定的类别，例如，对于一个图像分类任务，如果图像是“猫”，则对应的标签是 1 表示猫，0 表示狗和鸟。这种表示是确定性的。
   • 限制性：这种标签表示方式只能表明模型应当预测哪个类别，但无法提供类别之间的关系或“模糊”信息。如果两个类别之间很相似，模型难以通过这种硬标签理解这种相似性。

2. 概率分布即“知识”：

   • 概率分布：模型输出的概率分布即携带着网络的“知识”。概率分布可以在多个类别之间传递信息，例如，模型可能预测一个图像的类别是猫（概率为0.6），同时狗的概率为0.3，鸟的概率为0.1。这种分布不仅仅告诉我们最可能的类别（例如猫），还提供了类别之间的关系，表示“猫”和“狗”在模型中的相似度（0.3 的概率），而不是仅仅将这两个类别对立起来。

3. 通过KLD损失传递定位知识：

   • 定位知识（Localization Knowledge）：教师模型输出的概率分布携带了更多的信息，不仅是每个类别的预测概率，还包含了类别之间的相对关系（比如，猫和狗是相似的）。这些信息能够帮助学生模型更好地理解任务，尤其是在类别之间存在一定相似性的情况下。
   • 通过计算 KLD 损失，学生模型在训练过程中能够从教师模型的概率分布中“蒸馏”出这种额外的知识，从而提高性能。

2.一致的优化目标:由于 FDR 架构中每一个解码层都共享一个共同目标:减少初始边界框与真实边界框之间的残差;因此最后一层生成的精确概率分布可以作为前面每一层的最终目标，并通过蒸馏引导前几层。于是，基于 FDR，我们提出了 GO-LSD(全局最优定位自蒸馏)。通过在网络层间实现定位知识蒸馏，进一步扩展了D-FINE 的能力，具体流程如图: 这产生了一种双赢的协同效应:随着训练的进行，最后一层的预测变得越来越准确，其生成的软标签能够更好地帮助前几层提高预测准确性。反过来，前几层学会更快地定位到准确位置，简化了深层的优化任务，进一步提高了整体准确性。

对第2点的解释：

在 FDR 架构中，每一个解码层都有相同的目标，即将初始预测的边界框与真实边界框之间的误差（残差）尽可能减少。也就是说，无论是早期层还是最后一层，它们都在试图不断优化和精细化边界框的位置。

具体解释如下：

1. 一致的优化目标

   • FDR 架构中的所有解码层都致力于减少初始边界框与真实边界框之间的残差。这种一致性意味着，每一层都在解决同一个问题——如何使预测更精确。因此，所有层的最终目标是一致的，不论它们处于网络的哪个阶段。

2. 最后一层的精确输出作为目标

   • 最后一层通常经过多次迭代和优化，其输出的概率分布（即对边界框位置的置信度及调整信息）最为准确。因此，我们可以将这一层生成的精确概率分布视为“黄金标准”，作为前面所有解码层学习和优化的目标。

3. 通过蒸馏引导前几层

   • 知识蒸馏的核心思想是：利用“教师”（在这里是最后一层精确的输出）来指导“学生”（前几层）的学习。通过计算各层输出与最后一层输出之间的差异（比如使用 KL 散度损失），前几层可以逐步调整自己的输出，使之向最后一层的精确分布靠拢。这种做法能让整个网络在不同层次上保持一致的定位能力。

4. GO-LSD：全局最优定位自蒸馏

   • 基于 FDR 架构中这种层与层之间共享同一优化目标的特点，研究者提出了 GO-LSD（Global Optimal Localization Self-Distillation）。
   • GO-LSD 利用网络中各层之间一致的定位目标，将最后一层生成的最优概率分布通过自蒸馏的方法传递给前面的各个层级。这种全局性的定位知识蒸馏，不仅使每个解码层都能受益于最后一层的优化成果，同时也进一步提升了整体模型的定位能力。
   • 通过这种方式，D-FINE（在该背景下的某个基础模型或方法）的性能被进一步扩展和提升，因为每一层都在不断校正和优化，最终实现了全局最优的边界框定位效果。

GO-LSD 通过以下方式优化整个目标检测模型：

每层局部匹配：使用匈牙利匹配找到每一层的最佳边界框预测。

跨层最优匹配：整合所有层的匹配信息，选择全局最优的边界框，并让其他层向其学习（蒸馏）。

优化未匹配的预测： GO-LSD 通过优化这些未匹配预测，例如： 让它们向正确的匹配目标靠拢，或者 通过损失函数（如 Focal Loss）降低它们的权重，以减少错误影响。提高训练稳定性，使整个网络更鲁棒。 最终，整个网络在所有层次上都能学到更一致的高质量定位知识，提升检测精度和稳定性。
我们举个简单的例子来方便理解，

步骤1：各层的局部匹配

• Layer 1 （解码器第一层）输出了候选边界框 A、B、C，对应与 GT 的 IoU 分别为 0.60、0.45、0.55。

  • 匈牙利匹配在这一层选择 IoU 最高的候选框 A 作为匹配结果。

• Layer 2 输出了候选边界框 D、E、F，其与 GT 的 IoU 分别为 0.70、0.65、0.50。

  • 匈牙利匹配选出候选框 D（IoU 0.70）作为最佳匹配。

• Layer 3 输出了候选边界框 G、H、I，与 GT 的 IoU 分别为 0.55、0.80、0.60。

  • 匈牙利匹配选出候选框 H（IoU 0.80）作为匹配结果。

每一层都独立进行了匹配，得到了局部最优的预测：

• Layer 1：A
• Layer 2：D
• Layer 3：H

步骤2：全局匹配索引的聚合

GO-LSD 将三个层得到的匹配索引（A、D、H）合并成一个联合集。这个联合集包含了跨层最优秀的候选预测。这里，虽然三个层都有匹配结果，但在全局来看，候选框 H 在 IoU 上表现最好，被认为是全局最优的定位结果。

步骤3：利用全局最佳进行蒸馏和优化

• 蒸馏指导：

  • 将全局最佳候选框 H 作为“教师”输出，前面各层的匹配结果（如 A 和 D）通过计算 KL 散度等损失，被引导逐步调整，使得它们的预测分布向候选框 H 靠拢。
  • 这样，即使 Layer 1 和 Layer 2 的初始预测较弱，也能通过这种跨层指导逐步改善。

• 未匹配预测的优化：

  • 除了匹配成功的候选框外，每一层还可能有一些未匹配的候选预测（例如其他 IoU 较低的候选框），这些也会在训练过程中被优化，确保它们不会干扰整体预测，同时增强训练的稳定性。

然而这样有一个问题！！！
定位优化和分类匹配是两个独立的过程，联合集提升了定位精度，但分类任务仍然需要严格的一对一匹配，这会导致一些定位准确的分类预测置信度较低，需要进一步优化。

为了解决这个问题，我们引入了解耦蒸馏焦点(DDF)损失，它应用解耦加权策略来确保高iou但低置信度的预测被赋予适当的权重。DDF损失还根据匹配和不匹配预测的数量对它们进行加权，平衡它们的总体贡献和单个损失。这种方法使蒸馏更加稳定和有效。解耦蒸馏焦损失LDDF公式为:

解耦蒸馏焦点（DDF）损失 DDF，主要用于 优化知识蒸馏过程中高 IoU 但低置信度的预测框，以确保它们在蒸馏过程中得到合理的权重，同时平衡匹配（matched）和不匹配（unmatched）预测框的贡献。

T2是温度缩放系数，用于调整 KL 散度损失的平滑程度，确保软标签的信息更有效传递。 两部分损失： 匹配预测的蒸馏损失（第一项）:计算匹配目标（matched predictions）之间的 KL 散度损失。 权重𝛼K由 IoU 和匹配目标数量决定。 未匹配预测的蒸馏损失（第二项）计算未匹配目标（unmatched predictions）之间的 KL 散度损失。 权重 𝛽K由置信度和未匹配目标数量决定。
 

说白了，这个损失函数主要用于调节权重的，当框预测准确，分类预测置信度低时，传统的或许会放弃这个预测，但是这个损失函数加大了这个权重，使得它不被抛弃，相反，如果分类预测置信度高，框预测低，也会调整权重。

下面我们通过一个简单的例子来解释一下：

假设我们有两个预测框：

1. 框 A：IoU = 0.9，置信度 = 0.3
   • 这个框的定位很准，但分类置信度较低，传统方法可能会忽略它。
   • DDF 通过 IoU 赋予较高的权重，确保它仍然能有效学习。
2. 框 B：IoU = 0.4，置信度 = 0.9
   • 这个框的分类置信度高，但定位不够精准。
   • DDF 通过 置信度赋予适当的权重，确保它的分类能力能正确学习。

传统方法可能会直接忽略框 A，但 DDF 让 IoU 高的框仍然能被有效蒸馏，从而提高最终的检测性能。

实验结果我就不展示了，有需要论文的滴滴我就行