【信号处理】瑞利衰落通道上的差分MPSK研究(Matlab代码实现）

最新推荐文章于 2025-05-11 17:56:51 发布

Ps.729

最新推荐文章于 2025-05-11 17:56:51 发布

阅读量678

点赞数 21

文章标签：信号处理 matlab 算法

本文链接：https://blog.csdn.net/weixin_67304359/article/details/147822291

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

一、引言

二、瑞利衰落通道概述

三、差分MPSK基本原理

四、瑞利衰落通道上的差分MPSK性能分析

五、研究方法与仿真分析

六、结论与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

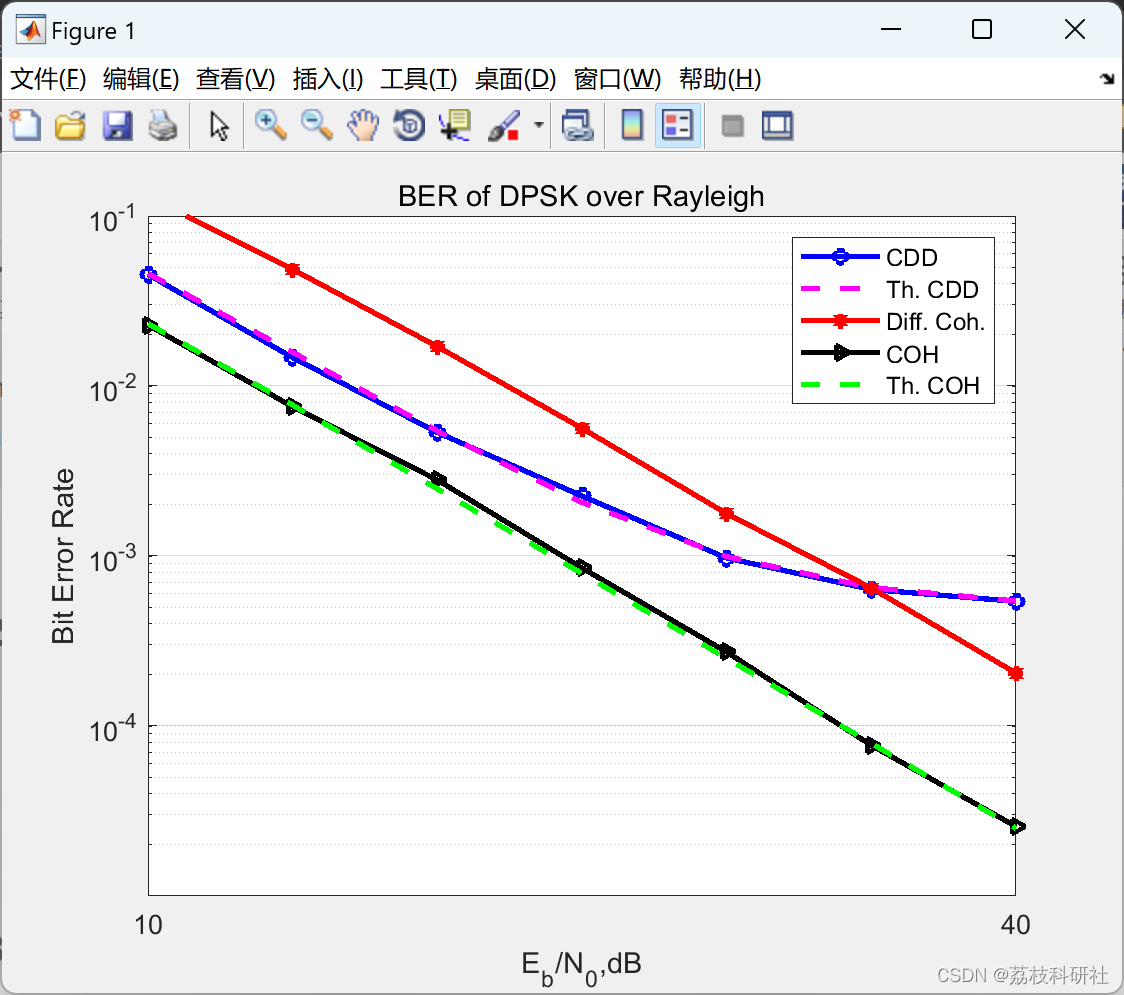
【信号处理】瑞利衰落通道上的差分MPSK研究

信号的调制识别是通信侦察、认知无线电等领域的关键技术，它在复杂环境和干扰噪声的情况下，不需要其他的先验知识，就能判断信号的调制方式，并提取相应的调制参数，为信号的进一步分析处理提供依据［1］。按调制识别依据理论的不同，可以分为依赖先验知识的判决论方法以及基于特征提取和分类器设计的统计模式识别方法。国内外众多学者在这方面做了大量的研究，各种调制识别方法也不断涌现。

时变瑞利衰落通道上的差分MPSK。通信是点对点的。源通过无线瑞利信道与目的地通信。通道是时变的。移动通信就是这种情况。自相关值决定了通道速度的大小。

Differential MPSK over time-varying Rayleigh fading channels. The communications is point to point. The source communicates with a destination through a wireless Rayleigh channel. The channel is time-varying. This is the case for mobile communications. Auto-correlation value determines the amount of channel speed.

一、引言

信号的调制识别在通信侦察、认知无线电等领域具有至关重要的作用。差分MPSK（Multiple Phase Shift Keying）作为一种重要的调制方式，在无线通信系统中得到了广泛应用。然而，无线通信系统常常面临着瑞利衰落等信道特性的挑战，这会对差分MPSK的性能产生影响。因此，研究瑞利衰落通道上的差分MPSK具有重要意义。

二、瑞利衰落通道概述

瑞利衰落是无线通信信道中的一种重要特性，它由于信号进行多径传播达到接收点处的场强来自不同传播的路径，各条路径延时时间是不同的，而各个方向分量波的叠加，又产生了驻波场强，从而形成信号快衰落。这种衰落属于小尺度的衰落效应，总是叠加于如阴影、衰减等大尺度衰落效应上。瑞利衰落信道模型在无线通信系统的设计和分析中具有重要意义。

三、差分MPSK基本原理

差分MPSK是一种相位调制方式，它通过改变载波的相位来表示不同的数据符号。差分MPSK具有抗噪声能力强、频谱利用率高等优点，在无线通信系统中得到了广泛应用。差分MPSK的调制方式包括BPSK（Binary Phase Shift Keying）、QPSK（Quadrature Phase Shift Keying）等，以及更高阶的MPSK调制方式，如8-PSK、16-PSK等。

四、瑞利衰落通道上的差分MPSK性能分析

误码率性能：
- 在瑞利衰落通道上，差分MPSK的误码率性能会受到信道特性的影响。信道衰落会导致信号幅度的波动，从而影响接收端的解调性能。
- 通过仿真和分析，可以研究不同阶数的MPSK在瑞利衰落通道上的误码率性能，并找出最优的调制阶数。
分集接收技术：
- 为了提高差分MPSK在瑞利衰落通道上的性能，可以采用分集接收技术。通过多个接收天线或中继节点来接收信号，并利用分集合并技术来提高接收信号的可靠性。
- 最大比合并（MRC）是一种常用的分集合并技术，它可以使合并后的输出信噪比达到最大。在瑞利衰落通道上，MRC分集接收可以显著提高差分MPSK的性能。
信道估计与均衡：
- 为了准确解调差分MPSK信号，需要对瑞利衰落通道进行准确的信道估计。信道估计的准确性会影响接收端的解调性能。
- 在信道估计的基础上，可以采用信道均衡技术来补偿信道失真，进一步提高差分MPSK的性能。

五、研究方法与仿真分析

仿真平台搭建：
- 利用MATLAB等仿真软件搭建瑞利衰落通道上的差分MPSK仿真平台。通过仿真平台，可以模拟不同的信道特性和调制参数，并观察差分MPSK的性能变化。
仿真参数设置：
- 在仿真过程中，需要设置合理的仿真参数，如符号数、信噪比范围、调制阶数等。这些参数的设置会影响仿真结果的准确性和可靠性。
仿真结果分析：
- 通过仿真结果，可以观察差分MPSK在瑞利衰落通道上的误码率性能、分集接收效果以及信道估计与均衡的改进效果。同时，还可以对仿真结果进行统计分析和比较，以得出有意义的结论。

六、结论与展望

通过对瑞利衰落通道上的差分MPSK的研究，可以得出以下结论：

差分MPSK在瑞利衰落通道上的性能受到信道特性的影响，但通过合理的参数设置和优化算法，可以显著提高性能。
分集接收技术和信道估计与均衡是提高差分MPSK性能的有效手段。

未来的研究方向可以包括以下几个方面：

探索更高效的信道估计与均衡算法，以进一步提高差分MPSK的性能。
研究差分MPSK与其他调制方式的结合应用，以拓展其应用范围。
深入研究瑞利衰落通道的特性和模型，为差分MPSK的优化设计提供理论支持。

📚2 运行结果

部分代码：

% total symbol error probability for D-AF with R-rleys

function Ps=Ps_multi_node(P,M,fsr,frd,R)
% inputs
% P : source power
% M : M-PSK constelastion
% fsr & frd : normalized doppler for source-relay and relay-destination
% R : number of relays
% output
% Ps : total symbol error probability

% amplification factor
global A2;

% autocorelations of individual and cascaded channel
alfa1=besselj(0,2*pi*fsr*(R+1));
alfa2=besselj(0,2*pi*frd*(R+1));
alfa=alfa1*alfa2;

% minimum distance in M-PSK
dmin=2*sin(pi/M);

% compute theoritical SER
% c=alfa^2*A2.*P;
% b=4;
% a=2*(1-alfa^2)*A2.*P+4*A2;
% beta=2*b./(c*dmin^2+2*a);
% d=c*dmin^2./(c*dmin^2+2*a);
%Ex_F_gama=d.*ex_fgama(beta,1);

temp=4*(1-alfa^2)+alfa^2*dmin^2;
K=P.*A2*temp+8*A2;
H=8./K;
Ex_F_gama=alfa^2*dmin^2*H.*P.*A2.*(1-exp(H).*H.*expint(H))/8;
Ex=1-Ex_F_gama;
sumEx=0;
for l=0:R-1
sumEx=sumEx+nchoosek(2*l,l)*(Ex/4).^l;
end
Ps=.5*(1-sqrt(Ex_F_gama).*sumEx);

% nearest neighbour approximation when M>2
if M>2
Ps=2*Ps;
end

end
%% subfunction integral x^R/(x+beta) exp(-x) dx, x=0 to inf
function out=ex_fgama(beta,R)

temp=0;
for k=1:R
temp=temp+factorial(R-1)*(-beta).^(R-k);
end
out=(temp+(-1)^R*beta.^R.*exp(beta).*expint(beta))/factorial(R-1);

end